Bu tip problemlerde rakamlardan oluşan bir kümenin elemanları kullanılarak belirtilen koşulları sağlayan kaç farklı sayı oluşturulabileceği hesaplanır.
Permütasyon bir kümenin elemanlarının her eleman bir kez kullanılacak şekilde farklı dizilişidir. Bu soruda rakamların tekrarlı kullanımı söz konusu olduğu için permütasyon formüllerini kullanamayız.
(a) seçeneği:
Rakamlar tekrarlı kullanılabildiği için her basamakta 5 rakam da kullanılabilir.
(b) seçeneği:
Rakamlar tekrarlı kullanılabildiği için ilk üç basamakta 5 rakam da kullanılabilir, son basamakta ise sadece çift rakamlar kullanılabilir.
(c) seçeneği:
Soldan ve sağdan okunuşu aynı olan 5 basamaklı sayılara örnek olarak 12321, 51515 ve 33333 verilebilir. Bu şekildeki sayılarda sadece ilk 3 basamak için rakam seçmemiz yeterlidir, çünkü sayının soldan ve sağdan okunuşlarının aynı olması için 4. basamak 2. basamakla, 5. basamak da 1. basamakla aynı olmalıdır, dolayısıyla 4. ve 5. basamaklar için sadece birer seçenek olacaktır.
Rakamları basamaklara soldan sağa doğru yerleştirdiğimizi varsayalım. 1. basamak için 5 seçenek vardır ve sağa doğru ilerledikçe her basamakta seçenek sayısı bir azalır. Örneğin, 1. basamakta "1" rakamı kullanıldıysa 2. basamak için kalan seçenekler \( \{2, 3, 4, 5\} \) olur.
Her basamak için seçenek sayılarını çarptığımızda istenen koşulu sağlayan sayı adedini buluruz.
(b) seçeneği:
Soruda 4. basamakla ilgili bir koşul verildiği için rakamları yerleştirmeye bu basamaktan başlamamız gerekir. 4. basamak için \( A \) kümesindeki tek rakamlar olmak üzere 3 seçenek vardır. 4. basamağa bu 3 rakamdan birini yazdıktan sonra 1. basamak için 4 seçenek kalır ve sağa doğru ilerledikçe her basamakta seçenek sayısı bir azalır.
Her basamak için seçenek sayılarını çarptığımızda istenen koşulu sağlayan sayı adedini buluruz.
Not: Rakamları yerleştirmeye 4. basamak dışında bir basamaktan (örneğin 1. basamaktan) başlarsak bir çift rakam seçmemiz durumunda 4. basamaktaki seçenek sayısı 3, tek rakam seçmemiz durumunda ise 2 olacaktır. Bir basamakta yaptığımız seçim diğer bir basamaktaki seçenek sayısını değiştirdiği için de çarpma kuralını kullanamayız.
(c) seçeneği:
Soruda 1. basamakla ilgili bir koşul verildiği için rakamları yerleştirmeye bu basamaktan başlamamız gerekir. Sayının 3000'den büyük olması için 1. basamağın \( \{3, 4, 5\} \) rakamlarından biri olması gerekir. 1. basamağa bu 3 rakamdan birini yazdıktan sonra diğer basamaklar için 4 seçenek kalır ve sağa doğru ilerledikçe her basamakta seçenek sayısı bir azalır.
Her basamak için seçenek sayılarını çarptığımızda istenen koşulu sağlayan sayı adedini buluruz.
(d) seçeneği:
Soruda 4. basamakla ilgili bir koşul verildiği için rakamları yerleştirmeye bu basamaktan başlamamız gerekir. Sayının 5'e tam bölünmesi için 4. basamak \( A \) kümesinin elemanları içinden sadece 5 olabilir. 4. basamağa "5" yazdıktan sonra 1. basamak için 4 seçenek kalır ve sağa doğru ilerledikçe her basamakta seçenek sayısı bir azalır.
Her basamak için seçenek sayılarını çarptığımızda istenen koşulu sağlayan sayı adedini buluruz.
0 rakamını içeren kümelerin permütasyonlarında 0 rakamının ilk basamakta kullanımının sayının basamak sayısını bir eksilteceği dikkate alınmalıdır.
(a) seçeneği:
1. basamakta 0 rakamını kullanmamız durumunda sayı 3 basamaklı olacağı için bu basamakta seçenek sayısı 5 değil 4 olur. 1. basamağa 0 dışındaki 4 rakamdan birini yazdıktan sonra 2. basamak için 4 seçenek kalır ve sağa doğru ilerledikçe her basamakta seçenek sayısı bir azalır.
Her basamak için seçenek sayılarını çarptığımızda istenen koşulu sağlayan sayı adedini buluruz.
(b) seçeneği:
1. basamak için yine 4 seçenek, 4. basamak için de \( B \) kümesindeki tek rakamlar olmak üzere 2 seçenek vardır. 4. basamaktaki seçenekler 1. basamaktaki seçeneklerin bir alt kümesi olduğu için, 4. basamakta hangi rakamı seçersek seçelim 1. basamaktaki seçenek sayısı bir eksilecektir, dolayısıyla ilk önce 4. basamak için bir rakam seçmemiz durumunda hangi rakam seçilirse seçilsin diğer basamakların seçenek sayıları değişmeyecektir.
Buna göre önce 4. basamak için 2 rakamdan biri seçilir, sonra 1. basamağa kullanılan rakam dışındaki 3 rakamdan biri yazılır. Geriye 2. basamak için 3 seçenek, 3. basamak için 2 seçenek kalır.
Her basamak için seçenek sayılarını çarptığımızda istenen koşulu sağlayan sayı adedini buluruz.
(c) seçeneği:
1. basamak için yine 4 seçenek, 4. basamak için de \( B \) kümesindeki çift rakamlar olmak üzere 3 seçenek vardır. Önceki sorudan farklı olarak bu soruda 1. ve 4. basamaklardaki seçenekler hem ortak hem de farklı değerler içerir, dolayısıyla herhangi birinde yapacağımız seçim diğer basamaktaki seçenek sayısını etkiler. Örneğin 1. basamak için 2 seçersek 4. basamağın seçenek sayısı 2'ye düşecektir. 1. basamak için 3 seçmemiz durumunda ise 4. basamağın seçenek sayısı değişmeyecektir. Bu durum çarpma kuralını kullanmamıza engel teşkil eder, bu yüzden problemi iki alt probleme bölmemiz ve toplama kuralı ile her iki durumda bulduğumuz sayı adetlerinin toplamını almamız gerekir.
İlk durumda 4. basamakta 1. basamakta bulunmayan seçenekleri, ikinci durumda iki basamakta da bulunan seçenekleri dikkate alalım. 4. basamaktaki seçenek sayılarını bu şekilde iki duruma böldüğümüzde 4. basamak için yapacağımız seçim 1. basamaktaki seçenek sayısını etkilemeyecektir.
İki durum için sayı adetlerini topladığımızda soruda istenen toplam sayı adedini \( 24 + 36 = 60 \) olarak buluruz.
Yukarıda problemi 4. basamağın seçeneklerini ikiye bölerek çözdük. Problemi 1. basamağın seçeneklerini ikiye bölerek çözersek de aynı sonucu elde ederiz.
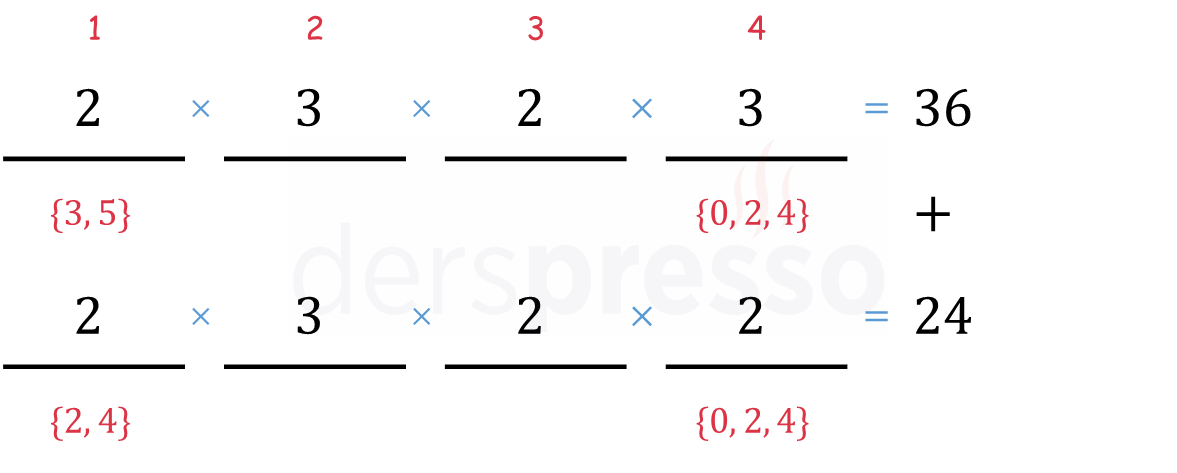
(d) seçeneği:
Bir sayının 5'e tam bölünmesi için birler basamağı 0 ya da 5 olmalıdır. Buna göre 1. basamak için seçenekler \( \{2, 3, 4, 5\} \), 4. basamak için de \( \{0, 5\} \) olur.
Bir önceki soruda olduğu gibi 1. ve 4. basamaklar hem ortak hem de farklı seçenekler içermektedir, dolayısıyla bir basamak için yapacağımız seçim diğer basamaktaki seçenek sayısını etkilemektedir. Bu yüzden problemi 4. basamak üzerinden ikiye bölelim ve toplama kuralı ile her iki durumda bulduğumuz sayı adetlerinin toplamını alalım.
İki durum için sayı adetlerini topladığımızda soruda istenen toplam sayı adedini \( 24 + 18 = 42 \) olarak buluruz.
Rakamları tekrarlı tüm sayıların rakamları tekrarsız tüm sayılardan farkı, en az iki basamağı aynı olan sayıların adedini verir.
[En az iki basamağı aynı olan sayı adedi] = [Rakamları tekrarlı tüm sayıların adedi] - [Rakamları tekrarsız tüm sayıların adedi]
Her iki sayı adedini yukarıdaki iki soruda sırasıyla \( 5^4 \) ve \( 120 \) olarak bulmuştuk. Bu iki sayının farkı en az iki basamağı aynı olan sayı adedini verir.
4 basamaklı toplam sayı adedini yukarıda \( 5! = 120 \) olarak bulmuştuk.
İçinde "3" bulunmayan 4 basamaklı sayı adedi, \( A \) kümesinin "3" elemanını içermeyen alt kümesi ile yazılabilecek 4 basamaklı sayı adedine, yani \( 4! \)'e eşittir.
Buna göre, istenen koşulu sağlayan \( 5! - 4! = 96 \) sayı yazılabilir.
2. yöntem:
Önce "3" rakamını 4 basamaktan birine \( 4 \) farklı şekilde yerleştirebiliriz.
Diğer 4 rakamın kalan 3 basamak için farklı diziliş sayısı \( P(4, 3) \) olur.
Buna göre, yazılabilecek sayı adedi \( 4 \cdot P(4, 3) = 96 \) olur.
Bu soruyu en pratik şekilde permütasyon ve kombinasyon yöntemlerini birlikte kullanarak çözebiliriz.
İstenen sayıların "1", "4" ve ek iki rakam içermesi gerektiğini biliyoruz, dolayısıyla "1" ve "4"ün zaten seçildiğini varsayalım. \( A \) kümesinin diğer 3 elemanı arasından 2 rakamı \( C(3, 2) \) farklı şekilde seçebiliriz.
"1", "4" ve seçtiğimiz diğer 2 rakam \( 4! \) farklı şekilde dizilebilir.
Son olarak, bu sayılardan kaçında "4" rakamının "1"in solunda olduğunu hesaplayalım. "1" ve "4" rakamları kendi aralarında \( 2! = 2 \) farklı şekilde dizilebilir ve "4" bunların birinde "1"in solunda, diğerinde sağındadır, dolayısıyla bulduğumuz toplam diziliş sayısını ikiye bölmemiz gerekir.
Buna göre istenen koşulu sağlayan \( \frac{C(3, 2) \cdot 4!}{2!} = 36 \) farklı sayı yazılabilir.
\( 4, 5, 6, 7, 8, 9 \) rakamları kullanılarak, yüz binler basamağı on binler basamağından büyük ve rakamları birbirinden farklı kaç tane 6 basamaklı sayı oluşturulabilir?
Yüz binler basamağına gelecek rakama göre 5 durum oluşur.
Durum 1: Yüz binler basamağı 9
Bu durumda on binler basamağı \( 8, 7, 6, 5, 4 \) olmak üzere 5 farklı değer alabilir. Kullanılan 2 rakam dışındaki 4 rakam kalan 4 basamağa yerleştirilir.
\( 1 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120 \) farklı sayı
Durum 2: Yüz binler basamağı 8
Bu durumda on binler basamağı \( 7, 6, 5, 4 \) olmak üzere 4 farklı değer alabilir. Kullanılan 2 rakam dışındaki 4 rakam kalan 4 basamağa yerleştirilir.
\( 1 \cdot 4 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 96 \) farklı sayı
Durum 3: Yüz binler basamağı 7
Bu durumda on binler basamağı \( 6, 5, 4 \) olmak üzere 3 farklı değer alabilir. Kullanılan 2 rakam dışındaki 4 rakam kalan 4 basamağa yerleştirilir.
\( 1 \cdot 3 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 72 \) farklı sayı
Durum 4: Yüz binler basamağı 6
Bu durumda on binler basamağı \( 5, 4 \) olmak üzere 2 farklı değer alabilir. Kullanılan 2 rakam dışındaki 4 rakam kalan 4 basamağa yerleştirilir.
\( 1 \cdot 2 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 48 \) farklı sayı
Durum 5: Yüz binler basamağı 5
Bu durumda on binler basamağı \( 4 \) olmak üzere 1 farklı değer alabilir. Kullanılan 2 rakam dışındaki 4 rakam kalan 4 basamağa yerleştirilir.
\( 1 \cdot 1 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 24 \) farklı sayı
Buna göre istenen koşulları sağlayan \( 120 + 96 + 72 + 48 + 24 = 360 \) farklı sayı oluşturulabilir.
Feyza 4 basamaklı, rakamları birbirinden farklı ve rakamları toplamı 26 olan tüm sayıları aralarında boşluk bırakmadan bilgisayarda yazıyor. Bilgisayarın klavyesindeki bir sorun nedeniyle 7 sayısına bir kez basıldığında ekrana iki tane 7 yazılıyor.
Buna göre Feyza tüm sayıları girdikten sonra ekranında yazan sayı, yazması gereken sayıdan kaç basamak fazladır?
Soldan sağa ve sağdan sola okunuşları aynı olan sayılara palindromik sayı denir.
Bu tanıma göre birler basamağında 4 olan 4 basamaklı palindromik sayı adedinin, onlar basamağında 7 olan 7 basamaklı palindromik sayı adedine oranı nedir?
\( a \) yerine 10 farklı rakam gelebileceği için bu şekilde 10 farklı sayı yazılabilir.
Onlar basamağında 7 olan 7 basamaklı palindromik sayılar \( (a7cdc7a) \) formundadır. \( a \) yerine 0 gelmesi sayıyı 6 basamaklı yapacağı için bu basamağa 9 farklı rakam gelebilir.
\( a \) yerine 9, \( c \) ve \( d \) yerine 10'ar farklı rakam gelebileceği için bu şekilde \( 9 \cdot 10 \cdot 10 = 900 \) farklı sayı yazılabilir.
Sayıların oranı \( \dfrac{10}{900} = \dfrac{1}{90} \) olarak bulunur.
2 basamağı asal olan ve 3 basamağı asal olan sayıları ayrı ayrı bulup toplamını alalım. 1 ve 4 asal olmadığı için 1 ve 4 basamağı asal olan sayıları dikkate almamıza gerek yoktur.
Durum 1: 2 basamak asal
Asal 4 rakam arasından 2 rakam \( C(4, 2) = 6 \) farklı şekilde seçilebilir.
Asal olmayan 6 rakam arasından 2 rakam \( C(6, 2) = 15 \) farklı şekilde seçilebilir.
Seçilen 4 rakam \( 4! = 24 \) farklı şekilde dizilebilir.
Buna göre 2 basamağı asal olan 4 basamaklı \( 6 \cdot 15 \cdot 24 = 2160 \) farklı sayı yazılabilir.
Ancak bu sayılardan binler basamağı 0 olanlar 3 basamaklı olacağı için bu sayıları bulduğumuz sayıdan çıkarmalıyız.
Binler basamağının 0 olduğunu varsayalım ve 0 içermeyen ve 2 basamağı asal olan 3 basamaklı kaç sayı olduğunu bulalım.
Asal 4 rakam arasından 2 rakam \( C(4, 2) = 6 \) farklı şekilde seçilebilir.
0 hariç asal olmayan 5 rakam arasından 1 rakam \( C(5, 1) = 5 \) farklı şekilde seçilebilir.
Seçilen 3 rakam \( 3! = 6 \) farklı şekilde dizilebilir.
Buna göre 2 basamağı asal olan ve 0 içermeyen 3 basamaklı \( 6 \cdot 5 \cdot 6 = 180 \) farklı sayı yazılabilir.
Bulduğumuz iki sayının farkı 2 basamağı asal olan 4 basamaklı sayı adedini verir.
\( 2160 - 180 = 1980 \)
Durum 2: 3 basamak asal
Asal 4 rakam arasından 3 rakam \( C(4, 3) = 4 \) farklı şekilde seçilebilir.
Asal olmayan 6 rakam arasından 1 rakam \( C(6, 1) = 6 \) farklı şekilde seçilebilir.
Seçilen 4 rakam \( 4! = 24 \) farklı şekilde dizilebilir.
Buna göre 3 basamağı asal olan 4 basamaklı \( 4 \cdot 6 \cdot 24 = 576 \) farklı sayı yazılabilir.
Ancak bu sayılardan binler basamağı 0 olanlar 3 basamaklı olacağı için bu sayıları bulduğumuz sayıdan çıkarmalıyız.
Binler basamağının 0 olduğunu varsayalım ve 0 içermeyen ve 3 basamağı asal olan 3 basamaklı kaç sayı olduğunu bulalım.
Asal 4 rakam arasından 3 rakam \( C(4, 3) = 4 \) farklı şekilde seçilebilir.
Seçilen 3 rakam \( 3! = 6 \) farklı şekilde dizilebilir.
Buna göre 3 basamağı asal olan ve 0 içermeyen 3 basamaklı \( 4 \cdot 6 = 24 \) farklı sayı yazılabilir.
Bulduğumuz iki sayının farkı 3 basamağı asal olan 4 basamaklı sayı adedini verir.
\( 576 - 24 = 552 \)
Soruda istenen sayıların adedi, bulduğumuz 2 basamağı asal olan sayılarla 3 basamağı asal olan sayıların toplamına eşittir.
Verilen 5 rakam kullanılarak 3 basamaklı \( 5 \cdot 4 \cdot 3 = 60 \) sayı yazılabilir. Herhangi 3 rakam aralarında \( 3! = 6 \) farklı şekilde dizilebilir ve bu 6 dizilişten sadece birinde \( a \gt b \gt c \) koşulu sağlanır. Buna göre yazılabilecek 60 sayıdan \( \frac{60}{3!} = 10 \) sayı verilen koşulu sağlar.
2. yöntem:
5 rakam içinden 3 rakam \( C(5, 3) = \frac{5!}{3!\ 2!} = 10 \) farklı şekilde seçilebilir. Seçilen her 3 rakam için \( a \gt b \gt c \) koşulunu sağlayan 3 basamaklı tek bir sayı yazılabilir, dolayısıyla cevap 10 olur.
\( A \) kümesinin elemanları ile 8 basamaklı ve rakamları farklı \( 8! \) sayı yazılabilir.
Bu sayılardan herhangi birini aldığımızda, \( 8! \) sayı içinde tek rakamların bu sayı ile aynı basamaklarda bulunduğu \( 4! \) farklı sayı vardır (4 rakamın kendi aralarındaki farklı diziliş sayısı kadar) ve bu \( 4! \) farklı dizilişten sadece birinde tek rakamlar küçükten büyüğe sıralanmıştır.
Dolayısıyla \( 8! \) sayının \( 4! = 24 \)'te birinde tek rakamlar küçükten büyüğe sıralanmıştır.
\( A = \{1, 2, 3, 4, 5, 6\} \) kümesinin elemanları ile yazılabilecek 4 basamaklı ve rakamları farklı sayılar küçükten büyüğe doğru sıralandığında, 268. sayının rakamları toplamı kaçtır?
\( A \) kümesinin elemanları ile 4 basamaklı ve rakamları farklı \( P(6, 4) = 6 \cdot 5 \cdot 4 \cdot 3 = 360 \) sayı yazılabilir.
Herhangi bir rakam ile başlayan sayı adedi, kalan 5 rakamla yazılabilecek 3 basamaklı sayı adedi kadar, yani \( P(5, 3) = 5 \cdot 4 \cdot 3 = 60 \) sayıdır.
Buna göre yazılabilecek 360 sayıdan 60'ı 1 ile, 60'ı 2 ile, ..., 60'ı 6 ile başlar.
Dolayısıyla sayılar küçükten büyüğe doğru sıralandığında 1. sayı 1 ile başlayan en küçük sayıdır.
61. sayı 2 ile başlayan en küçük sayıdır.
121. sayı 3 ile başlayan en küçük sayıdır.
181. sayı 4 ile başlayan en küçük sayıdır.
241. sayı 5 ile başlayan en küçük sayıdır, bu sayı da \( 5123 \) sayısıdır.
5 ile başlayan sayılardan 2. basamağı herhangi bir rakam olan sayı adedi, kalan 4 rakamla yazılabilecek 2 basamaklı sayı adedi kadar, yani \( P(4, 2) = 4 \cdot 3 = 12 \) sayıdır.
Buna göre 5 ile başlayan 60 sayıdan 12'si 51 ile, 12'si 52 ile, ..., 12'si 56 ile başlar.
241. sayı 51 ile başlayan en küçük sayıdır.
253. sayı 52 ile başlayan en küçük sayıdır.
265. sayı 53 ile başlayan en küçük sayıdır.
268. sayıyı bulmak istediğimiz için sırayla küçükten büyüğe sayıları sayalım.
265. sayı 5312 sayısıdır.
266. sayı 5314 sayısıdır.
267. sayı 5316 sayısıdır.
268. sayı 5321 sayısıdır.
Buna göre 268. sayının rakamları toplamı \( 5 + 3 + 2 + 1 = 11 \) olur.
\( 1, 2, 2, 3, 4 \) rakamları kullanılarak yazılabilecek beş basamaklı sayılar küçükten büyüğe doğru sıralandığında, 42132 sayısı baştan kaçıncı sırada olur?
Bu 5 rakam birer kez kullanılarak 5 basamaklı \( \frac{5!}{2!} = 60 \) farklı sayı yazılabilir.
Bu sayılar küçükten büyüğe sıralandığında sayıların ilk \( \frac{60}{5} = 12 \) tanesi 1 rakamı ile, ikinci ve üçüncü 12 tanesi 2 rakamıyla ve dördüncü 12 tanesi 3 ile başlar.
Buna göre 4 ile başlayan en küçük sayı, 49. sayı olan \( 41223 \) olur.
49. sayı dahil geri kalan sayıların ilk \( \frac{12}{4} = 3 \) tanesinin 2. basamağı 1'dir.
42 ile başlayan en küçük sayı, 52. sayı olan \( 42123 \) olur.
Buna göre \( 42132 \) sayısı bir sonraki, yani 53. sayı olur.
Rakamları soldan sağa arttığı için aşağıdaki sayılar istenen koşulu sağlar.
15, 379, 1579, 123456
Aşağıdaki sayılar ise istenen koşulu sağlamaz.
32, 668, 3079, 123454
Rakamlar artarak ilerleyeceği ve sıfır ilk basamakta bulunamayacağı için bu sayıların hiçbir basamağında sıfır bulunamaz.
Buna göre 1-9 arasındaki 9 rakamdan oluşan kümenin boş küme ve 1 elemanlı alt kümeleri hariç herhangi bir alt kümesinin elemanları ile istenen koşulu sağlayan tek bir sayı, alt kümedeki rakamlar küçükten büyüğe sıralanarak yazılabilir.
Bu tip problemlerde harflerden oluşan bir kümenin elemanları kullanılarak belirtilen koşulları sağlayan anlamlı ya da anlamsız kaç farklı kelime oluşturulabileceği hesaplanır.
SORU 25:
KİTAP kelimesinin harfleriyle anlamlı ya da anlamsız;
KİTAP kelimesinin harflerini bir küme olarak tanımlayalım.
\( A = \{K, İ, T, A, P\} \)
(a) seçeneği:
Bu kümenin 5 elemanlı her permütasyonu 5 harfli anlamlı ya da anlamsız bir kelimeye karşılık gelir.
(b) seçeneği:
Soruda kelimenin uzunluğu belirtilmediği için 1, 2, 3, 4 ve 5 harfli kelimelerin tümünü hesaplamaya dahil etmemiz gerekir (1 harfi de bir kelime olarak kabul ederek). Problemi bu şekilde 5'e bölerek her durum için yazılabilecek kelime sayısını aşağıdaki şekilde hesaplayabiliriz.
Her durum için kelime sayılarını topladığımızda yazılabilecek toplam kelime sayısını buluruz.
Bu soruyu en pratik şekilde permütasyon ve kombinasyonu birlikte kullanarak çözebiliriz.
(a) seçeneği:
Oluşturulacak kelimelerin "d" ve "e" harflerini içermesi gerektiğini biliyoruz. Diğer 6 harf içinden 3 harf \( C(6, 3) \) farklı şekilde seçilebilir.
"d" ve "e" harfleri ve seçilen ek üç harf \( 5! \) farklı şekilde dizilebilir.
Bu iki adımda elde ettiğimiz farklı durumların çarpımı toplam kelime sayısını verir.
\( C(6, 3) \cdot 5! = 20 \cdot 120 = 2400 \)
(b) seçeneği:
"d" ve "e" harflerine ek olarak üç harf \( C(6, 3) \) farklı şekilde seçilebilir.
"d" ve "e" harflerinin yan yana olması istendiği için bu iki harfi tek bir harf ve kelimeyi 3 harf ve 1 harf grubundan oluşan 4 harfli bir kelime olarak düşünebiliriz.
4 harfin farklı diziliş sayısı \( 4! \) olur. Bu dizilişlerin her birinde yan yana olan "d" ve "e" harfleri kendi aralarında \( 2! \) farklı şekilde yer değiştirebilir.
Bu üç adımda elde ettiğimiz farklı durumların çarpımı toplam kelime sayısını verir.
\( C(6, 3) \cdot 4! \cdot 2! = 960 \)
(c) seçeneği:
Oluşturulacak kelimelerin "a", "b" ve "c" harflerini içermesi gerektiğini biliyoruz. Diğer 5 harf içinden 2 harf \( C(5, 2) \) farklı şekilde seçilebilir.
"a", "b" ve "c" harflerinin yan yana olması istendiği için bu üç harfi tek bir harf ve kelimeyi 2 harf ve 1 harf grubundan oluşan 3 harfli bir kelime olarak düşünebiliriz.
3 harfin farklı diziliş sayısı \( 3! \) olur. Bu dizilişlerin her birinde yan yana olan "a", "b" ve "c" harfleri kendi aralarında \( 3! \) farklı şekilde yer değiştirebilir.
Bu üç adımda elde ettiğimiz farklı durumların çarpımı toplam kelime sayısını verir.
10 harfli DERSPRESSO kelimesinde "S" harfi üç kez, "E" ve "R" harfleri ikişer kez, diğer harfler birer kez bulunur.
(a) seçeneği:
DERSPRESSO kelimesinin farklı permütasyonlarının sayısını tekrarlı permütasyon formülü ile hesaplayalım.
\( \dfrac{10!}{3!\ 2!\ 2!} = 151200 \)
(b) seçeneği:
Kelimenin "D" harfi ile başlaması istendiği için ilk önce bu harfi kelimenin ilk harfi olarak ayıralım.
"D" harfi dışında kalan 9 harfle kaç kelime yazılabileceğini tekrarlı permütasyon formülü ile hesaplayalım.
\( \dfrac{9!}{3!\ 2!\ 2!} = 15120 \)
Bu kelimelerin her birinin başına "D" harfini eklediğimizde istenen koşulu sağlayan birer kelime elde etmiş oluruz.
(c) seçeneği:
Kelimenin "D" harfi ile başlayıp "P" harfi ile bitmesi istendiği için ilk önce bu iki harfi kelimenin ilk ve son harfi olarak ayıralım.
"D" ve "P" harfleri dışında kalan 8 harfle kaç kelime yazılabileceğini tekrarlı permütasyon formülü ile hesaplayalım.
\( \dfrac{8!}{3!\ 2!\ 2!} = 1680 \)
Bu kelimelerin her birinin başına "D" ve sonuna "P" harfini eklediğimizde istenen koşulu sağlayan birer kelime elde etmiş oluruz.
(d) seçeneği:
Bu soruda (c) seçeneğinde oluşturulan her kelimede "D" ve "P" harfleri kendi aralarında her değiştirebilir, dolayısıyla bulduğumuz farklı kelime sayısını \( 2! \) ile çarpmamız gerekir.
\( 1680 \cdot 2! = 3360 \)
(e) seçeneği:
Aynı harfleri kendi aralarında grupladığımızda DERSPO kelimesini elde ederiz.
Bu 6 harf ve harf grubu \( 6! = 720 \) farklı şekilde dizilebilir. Yan yana bulunan aynı harfler özdeş oldukları için kendi aralarında yer değiştirmeleri yeni birer diziliş oluşturmaz.
7 harfli ABARTMA kelimesinde "A" harfi üç kez, diğer harfler birer kez bulunur.
(a) seçeneği:
Üç "A" harfinin yan yana olmadığı diziliş sayısını aşağıdaki formülle bulabiliriz.
[Üç "A" harfinin yan yana olmadığı diziliş sayısı] = [Tüm farklı diziliş sayısı] - [Üç "A" harfinin de yan yana olduğu diziliş sayısı]
ABARTMA kelimesinin farklı permütasyonlarının sayısını tekrarlı permütasyon formülü ile hesaplayalım.
\( \dfrac{7!}{3!} = 840 \)
Üç "A" harfinin de yan yana olduğu diziliş sayısını hesaplayalım.
Üç "A" harfini kendi aralarında grupladığımızda ABRTM kelimesini elde ederiz.
Bu 5 harf ve harf grubu \( 5! = 120 \) farklı şekilde dizilebilir. Yan yana bulunan "A" harfleri özdeş oldukları için kendi aralarında yer değiştirmeleri yeni birer diziliş oluşturmaz.
Bulduğumuz iki sayının farkı üç "A" harfinin yan yana olmadığı diziliş sayısını verir.
\( 840 - 120 = 720 \)
(b) seçeneği:
Herhangi iki "A" harfinin yan yana olmadığı 10 durum vardır.
\( A\_A\_A\_\ \_ \)
\( A\_A\_\ \_A\_ \)
\( A\_A\_\ \_\ \_A \)
\( A\_\ \_A\_A\_ \)
\( A\_\ \_A\_\ \_A \)
\( A\_\ \_\ \_A\_A \)
\( \_A\_A\_A\_ \)
\( \_A\_A\_\ \_A \)
\( \_A\_\ \_A\_A \)
\( \_\ \_A\_A\_A \)
Bu 10 farklı durumun her birinde diğer BRTM harfleri 4 boşluğa \( 4! = 24 \) farklı şekilde yerleştirilebilir.
Buna göre istenen koşulu sağlayan \( 10 \cdot 24 = 240 \) farklı kelime yazılabilir.
KUYRUKSALLAYANGİLLER kelimesinde 20 harf vardır, bu harflerin 13'ü sessiz, 7'si seslidir.
Sessiz harfler: LLLLKKRRYYGNS
Sesli harfler: AAAUUEİ
Kelimedeki sesli harfleri bir grup olarak düşünelim. Buna göre 13 sessiz harf ve 1 sesli harf grubu için farklı permütasyon sayısını, sessiz harfler içinde tekrar eden harfleri dikkate alarak tekrarlı permütasyon formülü ile hesaplayalım.
\( \dfrac{14!}{4!\ 2!\ 2!\ 2!} \)
Bu dizilişlerin her birinde sesli harf grubundaki harflerin kendi aralarındaki farklı diziliş sayısını, yine tekrar eden harfleri dikkate alarak tekrarlı permütasyon formülü ile hesaplayalım.
\( \dfrac{7!}{3!\ 2!} \)
Bulduğumuz iki sayının çarpımı sesli harflerin yan yana olduğu toplam diziliş sayısını verir.
\( \dfrac{14!}{4!\ 2!\ 2!\ 2!} \cdot \dfrac{7!}{3!\ 2!} \) bulunur.
8 harfli GODZILLA kelimesinde "L" harfi iki kez, diğer harfler birer kez bulunur.
Bu kelimenin harfleri ile 8 harfli kaç kelime oluşturulabileceği sorulmuş olsa cevap tekrarlı permütasyon formülü ile \( \frac{8!}{2!} \) olurdu.
Ya da kelimede her harf bir kez bulunuyor olsa 4 harfli \( P(8, 4) \) farklı kelime yazılabilirdi.
Hem bir harfin tekrarladığı hem de oluşturulacak kelimelerde harflerden sadece dördünün kullanılacağı durumda tüm kelimelerin sayısını tek bir adımda hesaplayamayız.
Problemi 4 harfli kelimelerin hiç "L" harfi içermemesi, bir "L" harfi içermesi ve iki "L" harfi içermesi şeklinde üç durum altında inceleyelim.
Durum 1: 4 harfli kelimede "L" harfi yok
"L" harfi hariç GODZIA harfleri ile 4 harfli \( P(6, 4) \) farklı kelime yazılabilir.
\( P(6, 4) = 360 \)
Durum 2: 4 harfli kelimede bir "L" harfi
GODZIA harflerinden üç harf \( C(6, 3) \) farklı şekilde, LL harflerinden bir harf \( 1 \) farklı şekilde seçilebilir. Seçilen bu 4 harf aralarında \( 4! \) farklı şekilde dizilebilir.
\( C(6, 3) \cdot 1 \cdot 4! = 480 \)
Durum 3: 4 harfli kelimede iki "L" harfi
GODZIA harflerinden iki harf \( C(6, 2) \) farklı şekilde, LL harflerinden iki harf \( 1 \) farklı şekilde seçilebilir. Seçilen bu 4 harf aralarında tekrarlı permütasyon formülü ile \( \frac{4!}{2!} \) farklı şekilde dizilebilir.
\( C(6, 2) \cdot 1 \cdot \dfrac{4!}{2!} = 180 \)
4 harfli farklı kelime sayısı bu üç durum için bulduğumuz kelime sayılarının toplamına eşittir.
DENİZ kelimesinin harflerinin alfabetik dizilişi DEİNZ şeklinde olur.
DENİZ kelimesinin harfleri ile anlamlı ya da anlamsız \( 5! = 120 \) farklı kelime yazılabilir.
Bu kelimelerden "D" harfi ile başlayanların sayısı, diğer 4 harfin farklı diziliş sayısı kadar, yani \( 4! = 24 \) adettir.
Buna göre 120 kelimenin 24'ü "D" ile, 24'ü "E" ile, ..., 24'ü "Z" ile başlar.
Dolayısıyla 1. kelime "D" harfi ile başlayan ilk kelime, 25. kelime "E" harfi ile başlayan ilk kelime, 49. kelime "İ" harfi ile başlayan ilk kelime, 73. kelime de "N" harfi ile başlayan ilk kelimedir.
73. kelime NDEİZ olur.
"N" ile başlayan kelimelerden 2. harfi "D" olanların sayısı, diğer 3 harfin farklı diziliş sayısı kadar, yani \( 3! = 6 \) adettir.
Buna göre "N" ile başlayan 24 kelimenin 6'sının 2. harfi "D", 6'sının 2. harfi "E", ..., 6'sının 2. harfi "Z" olur.
Dolayısıyla 73. kelime "ND" harfleri ile başlayan ilk kelime, 79. kelime "NE" harfleri ile başlayan ilk kelime, 85. kelime "Nİ" harfleri ile başlayan ilk kelime, 91. kelime de "NZ" harfleri ile başlayan ilk kelimedir.
