Düzgün Çokgenler
Tüm kenarlarının uzunlukları ve iç açılarının ölçüleri eşit olan, diğer bir deyişle hem eşkenar, hem de eş açılı olan çokgenlere düzgün çokgen denir.
Düzgün Çokgenlerin Açı Özellikleri
\( n \) kenarlı bir düzgün çokgenin bir açı açısının ölçüsü aşağıdaki formülle bulunabilir.
\( \text{Çokgenin iç açıları toplamı} = (n - 2) \cdot 180° \)
\( \text{Bir iç açı ölçüsü} = \dfrac{(n - 2) \cdot 180°}{n} \)
Düzgün sekizgenin bir iç açısının ölçüsü:
\( \text{Bir iç açı ölçüsü} = \dfrac{(8 - 2) \cdot 180°}{8} = 135° \)
\( n \) kenarlı bir düzgün çokgenin bir dış açısının ölçüsü aşağıdaki formülle bulunabilir.
\( \text{Bir dış açı ölçüsü} = \dfrac{360°}{n} \)
Düzgün sekizgenin bir dış açısının ölçüsü:
\( \text{Bir dış açı ölçüsü} = \dfrac{360°}{8} = 45° \)
İç ve dış açılar toplamı her zaman 180° olduğu için, düzgün çokgenin bir iç açısını bulmak için alternatif bir yöntem olarak önce bir dış açı bulunup bu açının bütünler açısı bulunabilir.
Düzgün sekizgenin bir iç açısının ölçüsü:
\( \text{Bir dış açı ölçüsü} = \dfrac{360°}{8} = 45° \)
\( \text{Bir iç açı ölçüsü} = 180 - 45 = 135° \)
\( n \) çift sayı olmak üzere, \( n \) kenarlı bir düzgün çokgenin karşılıklı (uzak) köşeleri arasında çizilen köşegenler için aşağıdakiler doğrudur.
- Köşegenler düzgün çokgenin merkezinde tek bir noktada kesişirler.
- Her köşegen birleştirdiği köşelerin açıortayıdır.
- Köşegenler birbirini ortalar.
- Köşegenler düzgün çokgenin alanını \( n \) eşit bölgeye ayırır.
- Köşegenlerin kesişimi olan nokta, aynı zamanda düzgün çokgenin iç teğet ve çevrel çemberlerinin merkezidir.
Düzgün çokgenlerde aynı sayıda kenarı gören köşegenlerin uzunlukları birbirine eşittir.
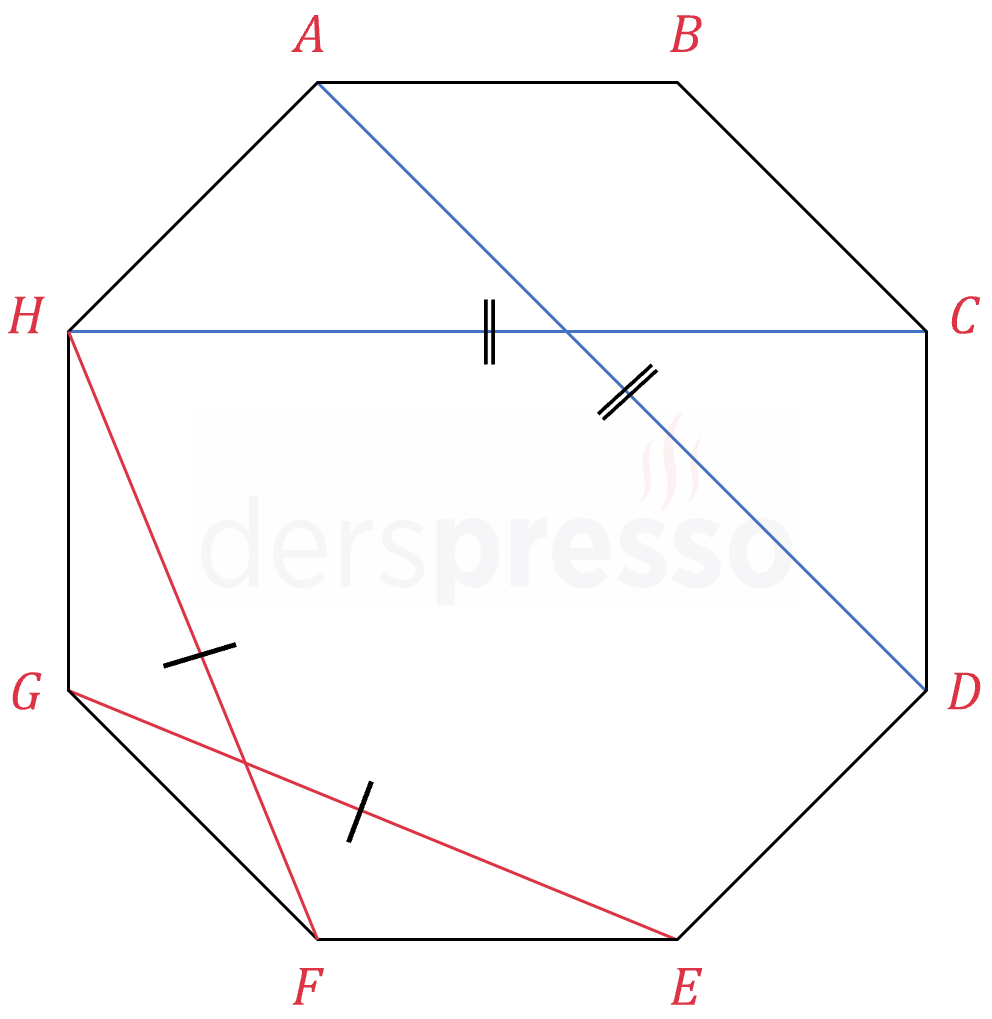
\( [AD] \) ve \( [HC] \) köşegenleri 3'er kenar görür.
\( \abs{AD} = \abs{HC} \)
\( [HF] \) ve \( [GE] \) köşegenleri 2'şer kenar görür.
\( \abs{HF} = \abs{GE} \)
\( n \) çift sayı olmak üzere, \( n \) kenarlı çokgenlerde karşılıklı kenarlar birbirine paraleldir.
En Sık Kullanılan Düzgün Çokgenler
| Şekil | İç Açılar Toplamı | Bir İç Açı Ölçüsü | Dış Açılar Toplamı | Bir Dış Açı Ölçüsü |
|---|---|---|---|---|
|
Düzgün Çokgen
|
\( (n - 2) \cdot 180° \) | \( \dfrac{(n - 2) \cdot 180°}{n} \) | \( 360° \) | \( \dfrac{360°}{n} \) |
|
Eşkenar Üçgen
|
\( 180° \) | \( 60° \) | \( 360° \) | \( 120° \) |
|
Kare
|
\( 360° \) | \( 90° \) | \( 360° \) | \( 90° \) |
|
Düzgün Beşgen
|
\( 540° \) | \( 108° \) | \( 360° \) | \( 72° \) |
|
Düzgün Altıgen
|
\( 720° \) | \( 120° \) | \( 360° \) | \( 60° \) |
|
Düzgün Sekizgen
|
\( 1080° \) | \( 135° \) | \( 360° \) | \( 45° \) |
Düzgün Altıgen
Düzgün altıgenin karşılıklı (uzak) köşeleri arası çizilen köşegenler aynı zamanda birleştirdikleri köşelerin açıortayı oldukları için, bu köşegenler 6 eşkenar üçgen oluştururlar.
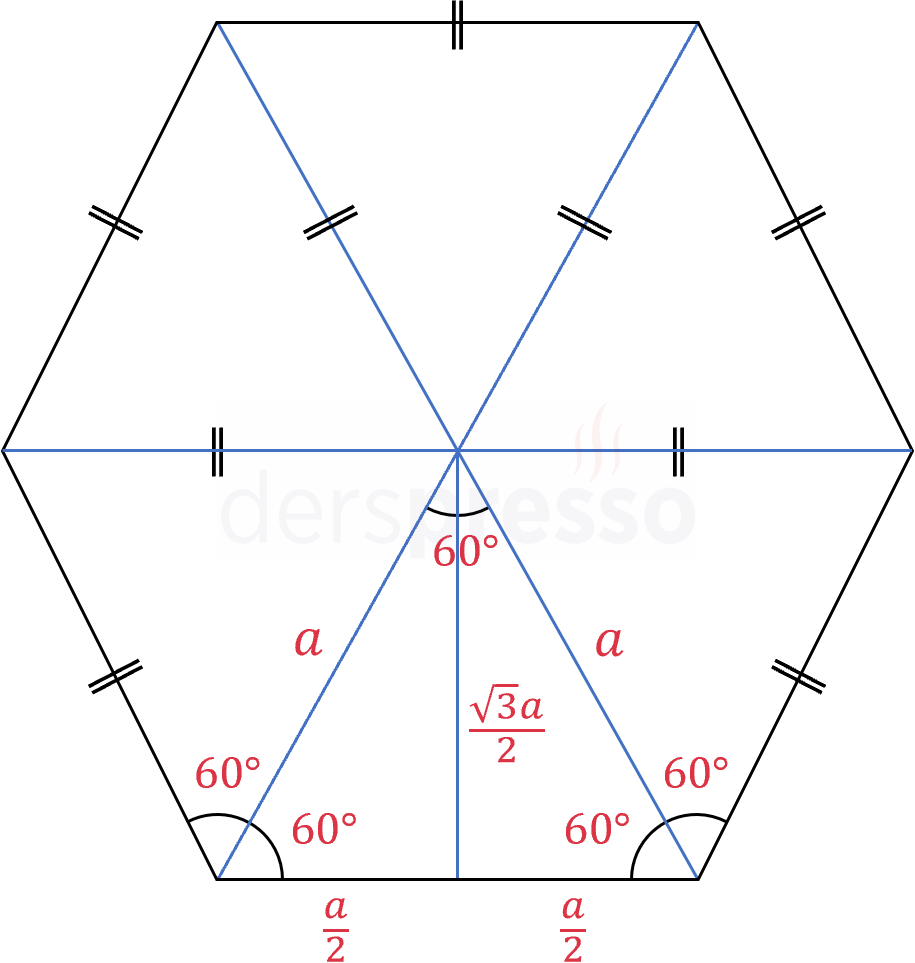
Düzgün altıgenin uzun köşegenlerinin her birinin uzunluğu altıgenin bir kenar uzunluğunun iki katına, kısa köşegenlerinin her birinin uzunluğu altıgenin bir kenar uzunluğunun \( \sqrt{3} \) katına eşittir.
Kısa köşegen uzunluğunu bulmak için kosinüs teoremini kullanalım.
Düzgün altıgenin bir iç açısının ölçüsü 120 derecedir.
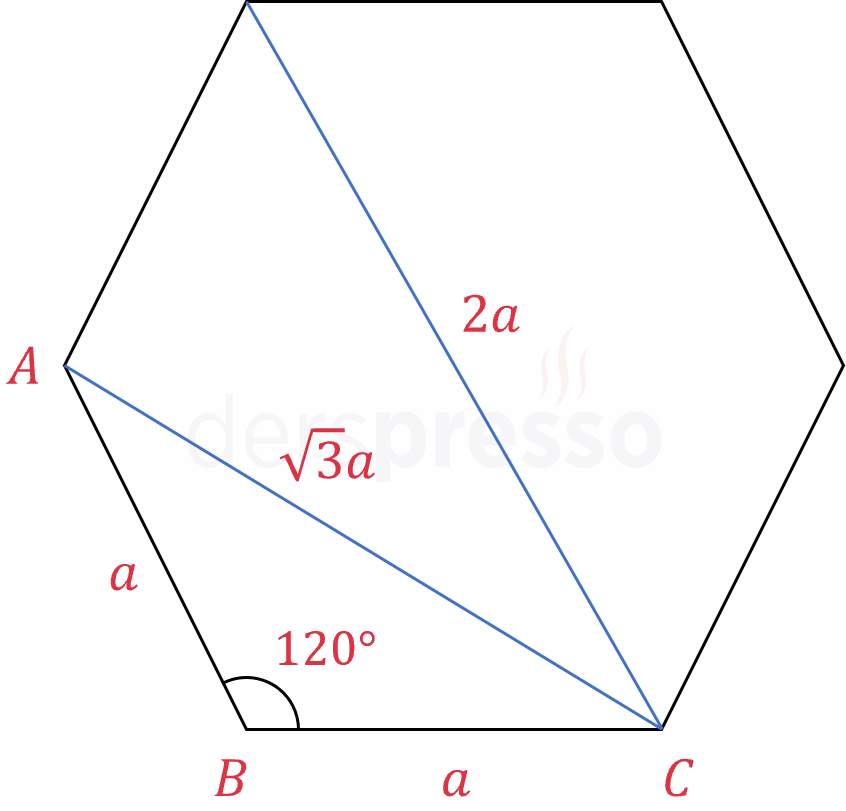
\( \abs{AC}^2 = a^2 + a^2 - 2a \cdot a \cdot \cos{120°} \)
\( = 2a^2 - 2a^2 \cdot (-\dfrac{1}{2}) \)
\( = 2a^2 + a^2 \)
\( = 3a^2 \)
\( \abs{AC} = \sqrt{3}a \)
Bir kenar uzunluğu \( a \) birim olan düzgün altıgenin alanını aşağıdaki formülle bulabiliriz.
\( \text{Bir eşkenar üçgenin yüksekliği} = \dfrac{\sqrt{3}a}{2} \)
\( \text{Bir eşkenar üçgenin alanı} = \dfrac{\sqrt{3}a^2}{4} \)
\( \text{Düzgün altıgenin alanı} = 6 \cdot \dfrac{\sqrt{3}a^2}{4} \)
Karşılıklı köşeler arası çizilen köşegenler, düzgün altıgenin alanını 6 eşit bölgeye ayırır.
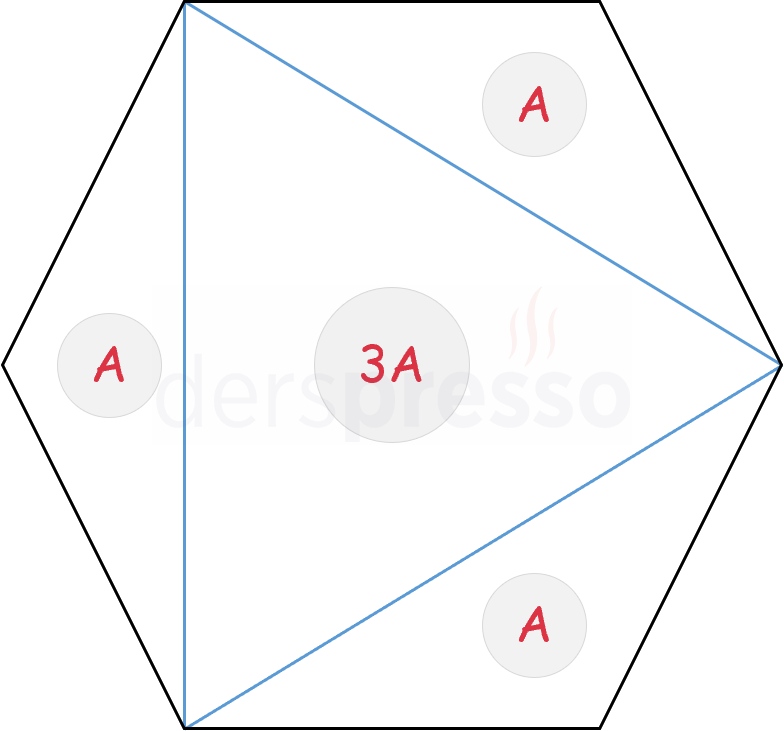
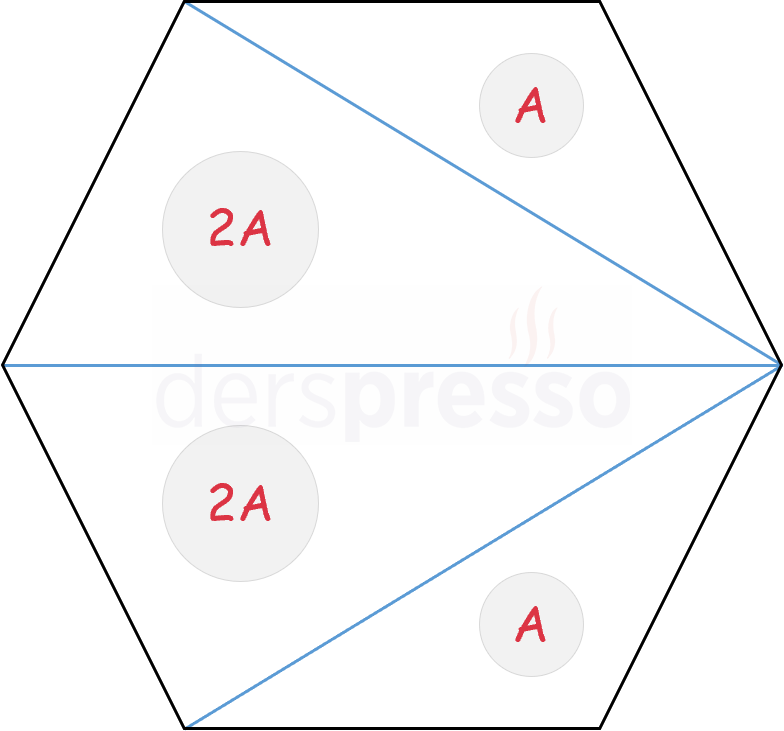
Bir düzgün altıgenin farklı noktaları arasında çizilen doğru parçaları, düzgün altıgenin alanını aşağıdaki oranlarda böler.
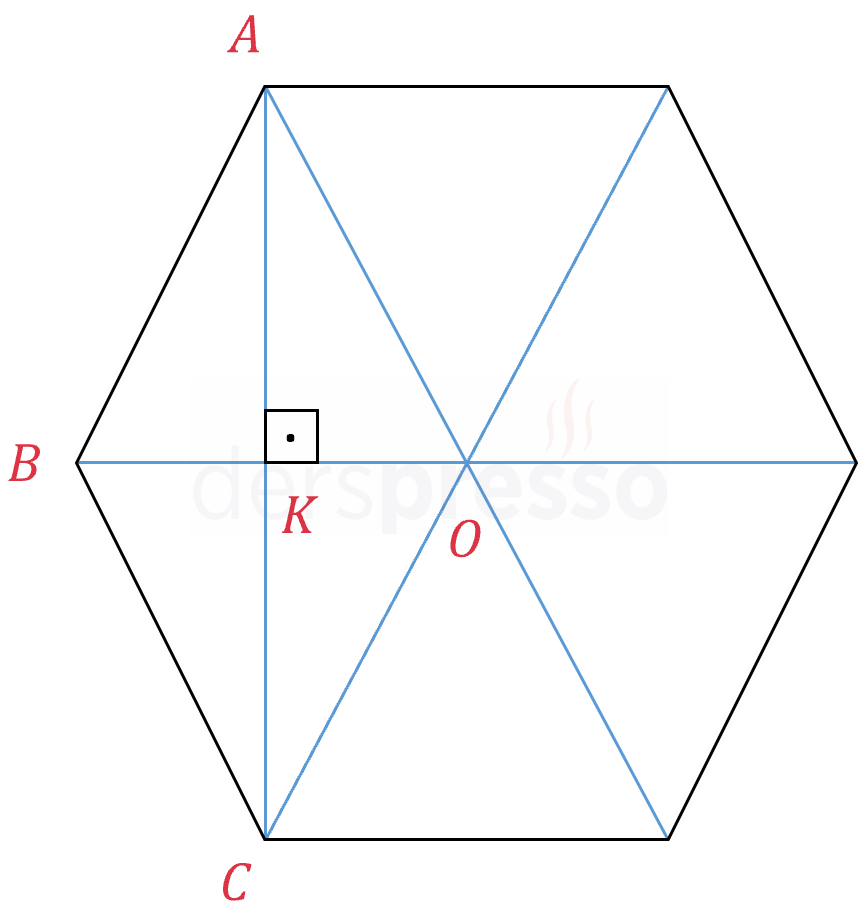
Kosinüs teoremini kullanarak \( \abs{AC} \) uzunluğunu bulalım.
\( \abs{AB} = \abs{BC} = a \)
\( m(\widehat{ABC}) = 120° \)
\( \abs{AC}^2 = a^2 + a^2 - 2a^2\cos{120°} \)
\( \abs{AC} = \sqrt{3} a \)
\( [AK] \) doğru parçası, \( \overset{\triangle}{ABO} \) üçgeninin yüksekliği ise, bu yüksekliğin uzunluğunu aşağıdaki gibi bulmuştuk.
\( \abs{AK} = \dfrac{\sqrt{3}a}{2} \)
\( \abs{AC} \) uzunluğunun \( \abs{AK} \)'nin iki katı olduğunu görüyoruz, buna göre bu iki doğru parçası çakışıktır ve \( [AC] \) doğru parçası aynı zamanda \( \overset{\triangle}{ABO} \) ve \( \overset{\triangle}{BCO} \) üçgenlerinin yüksekliği ve kenarortayıdır ve alanlarını ikiye böler. Bu yüzden, \( \overset{\triangle}{ABC} \) üçgeninin alanı, köşegenlerin oluşturduğu eşkenar üçgenlerden birinin alanına eşittir.
\( A(\overset{\triangle}{ABK}) = \dfrac{A(\overset{\triangle}{ABO})}{2} \)
\( A(\overset{\triangle}{ABC}) = 2 \cdot A(\overset{\triangle}{ABK}) \)
\( A(\overset{\triangle}{ABC}) = A(\overset{\triangle}{ABO}) \)
Düzgün Sekizgen
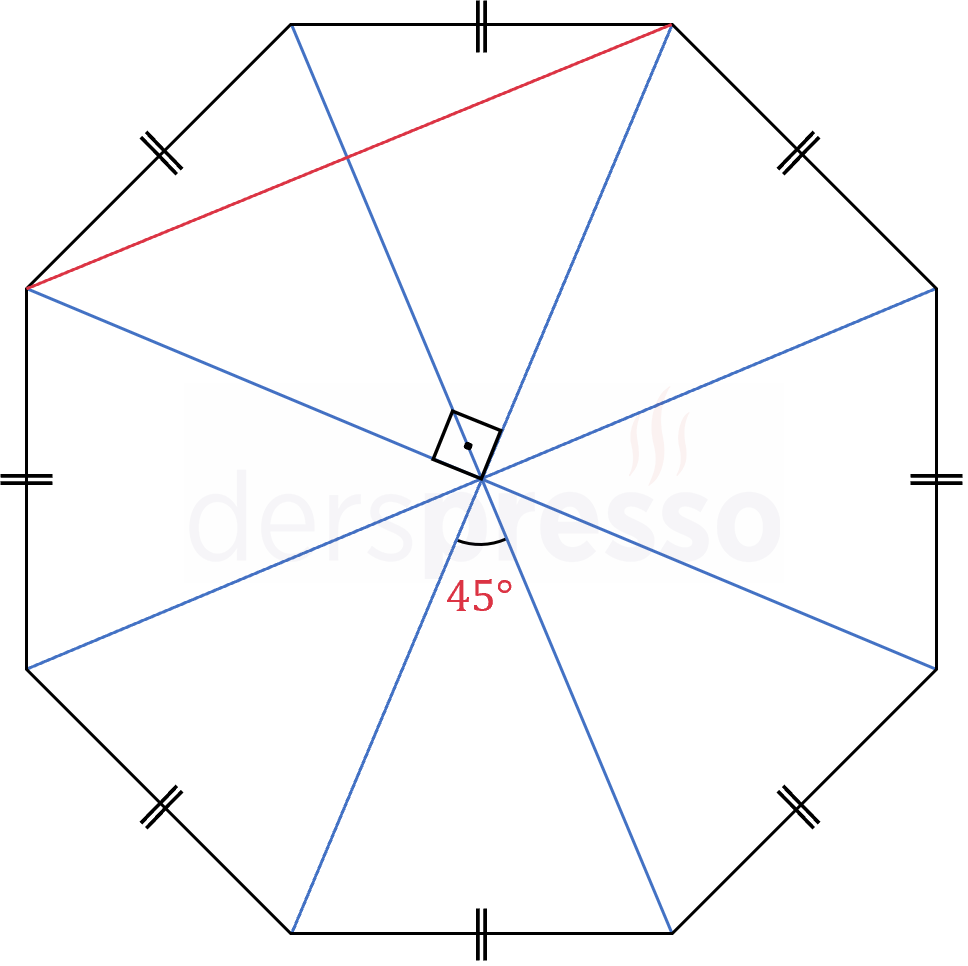
Düzgün sekizgende karşılıklı (uzak) köşeler arası çizilen köşegenlerin merkezde oluşturduğu açıların her biri \( \dfrac{360°}{8} = 45° \)'dir. Buna göre, bu şekilde oluşan açılardan iki tanesi bir dik açı oluşturur.
Karşılıklı köşeler arası çizilen köşegenler, düzgün sekizgenin alanını 8 eşit bölgeye ayırır.
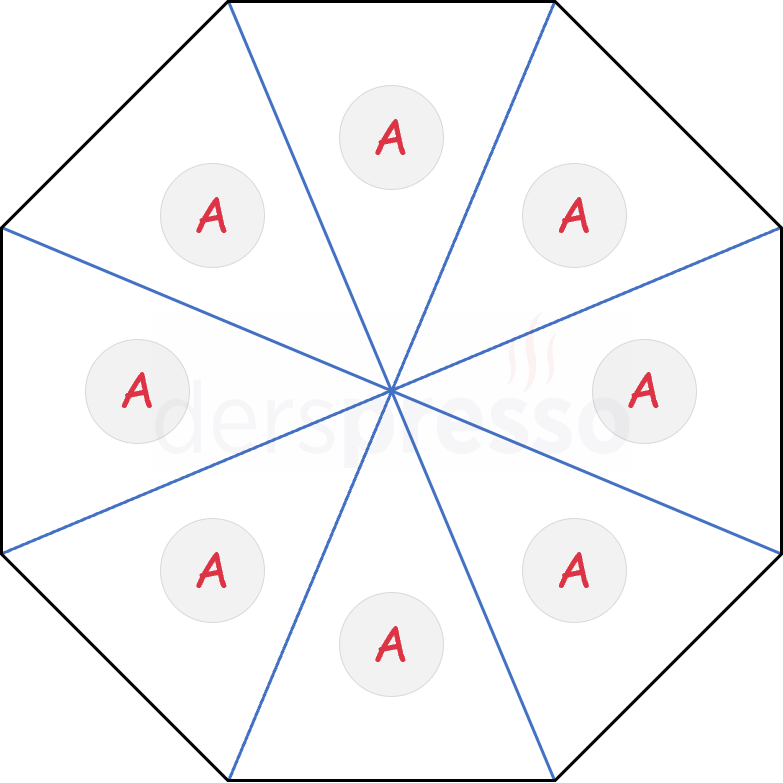
Bir düzgün sekizgenin farklı noktaları arasında çizilen doğru parçaları, düzgün sekizgenin alanını aşağıdaki oranlarda böler.
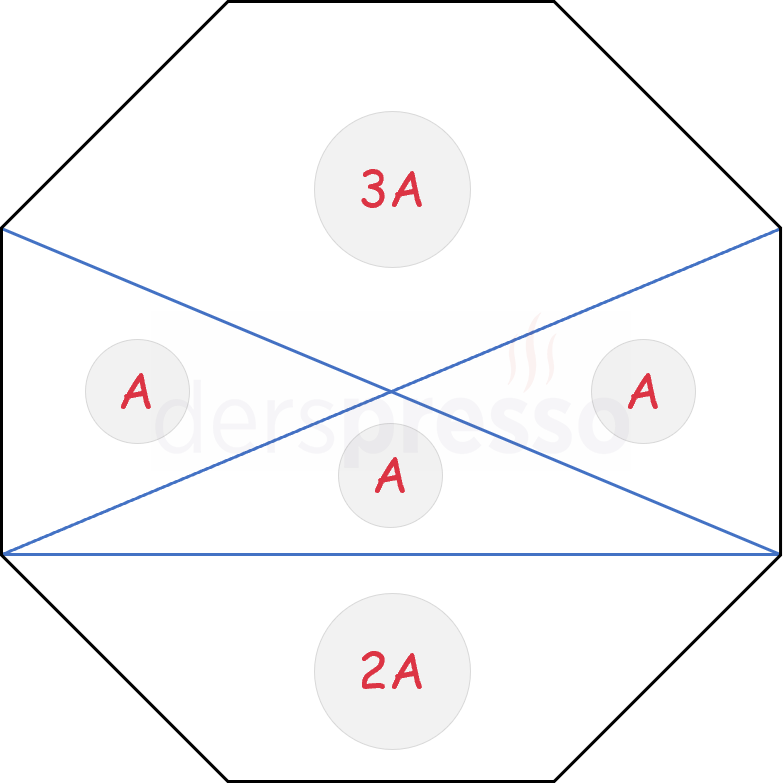
İç Teğet ve Çevrel Çemberler
Tüm düzgün çokgenlerin iç teğet çemberi vardır ve merkezi düzgün çokgenin merkezi ile aynı noktadır. Bir düzgün çokgenin iç teğet çemberinin yarıçap uzunluğu, çokgenin merkezinden herhangi bir kenarına çizilen dikmenin uzunluğuna eşittir.
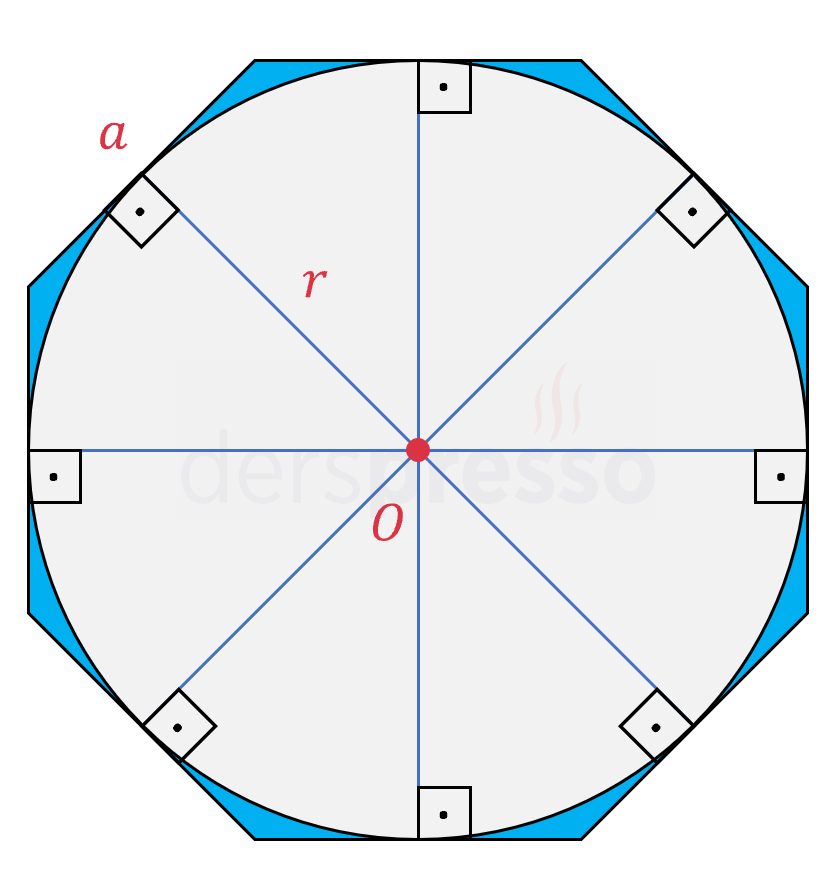
Bir kenar uzunluğu \( a \) olan \( n \) kenarlı düzgün çokgenin iç teğet çemberinin yarıçapı (\( r \)) ve düzgün çokgenin alanı aşağıdaki formüllerle bulunabilir.
\( r = \dfrac{a}{2\tan{\frac{\pi}{n}}} \)
\( A = \dfrac{nar}{2} \)
\( A = \dfrac{na^2}{4\tan{\frac{\pi}{n}}} \)
İSPATI GÖSTER
\( n \) kenarlı bir düzgün çokgenin merkezinden ardışık iki köşesine çizilen \( [OA] \) ve \( [OB] \) doğru parçaları şekildeki \( OAB \) ikizkenar üçgenini oluşturur.
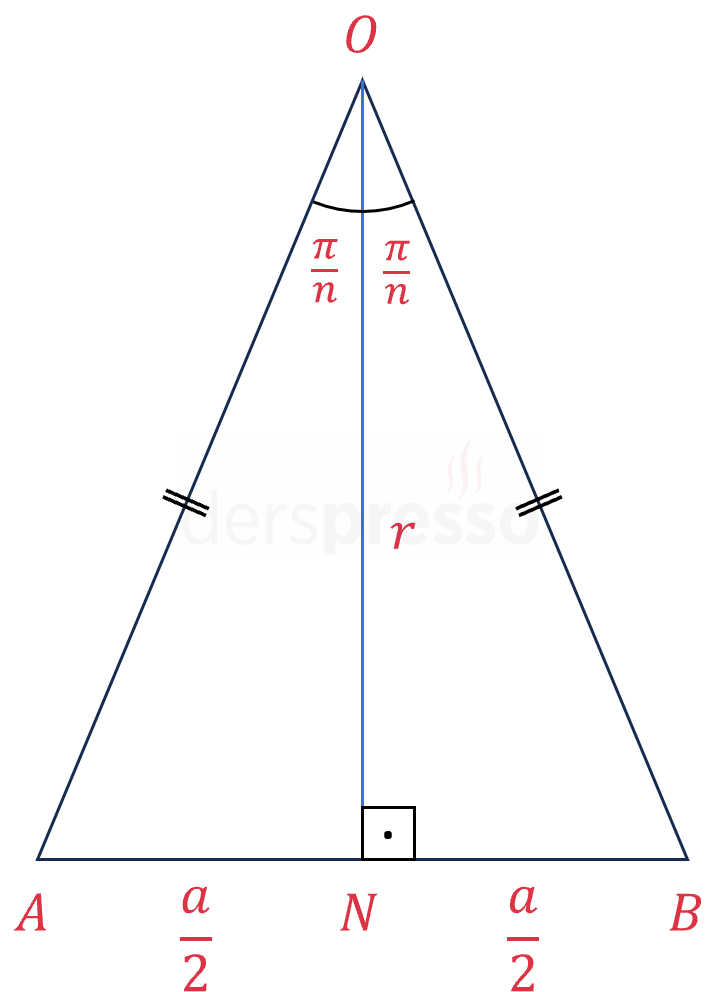
Düzgün çokgen bu üçgen ile eş \( n \) üçgenin biraraya gelmesiyle oluşur.
Üçgenin yüksekliği düzgün çokgenin iç teğet çemberinin yarıçapına eşittir.
\( \abs{ON} = r \)
Üçgenin tepe açısını bulalım.
\( m(\widehat{AOB}) = \dfrac{360°}{n} = \dfrac{2\pi}{n} \)
\( m(\widehat{AON}) = m(\widehat{NOB}) = \dfrac{\pi}{n} \)
İkizkenar üçgende yükseklik tabanı ortalar.
\( \abs{AN} = \abs{NB} = \dfrac{a}{2} \)
Trigonometrik oranları kullanarak iç teğet çemberin yarıçapını bulalım.
\( \tan{\frac{\pi}{n}} = \dfrac{\frac{a}{2}}{r} \)
\( r = \dfrac{a}{2\tan{\frac{\pi}{n}}} \)
Bu yarıçap değerini kullanarak düzgün çokgenin alanını bulalım.
Düzgün çokgenin alanı \( OAB \) üçgeninin alanının \( n \) katına eşittir.
\( A = n \cdot \dfrac{a \cdot r}{2} = \dfrac{nar}{2} \)
\( r \) değerini yerine koyalım.
\( A = \dfrac{na \cdot \frac{a}{2\tan{\frac{\pi}{n}}}}{2} \)
\( A = \dfrac{na^2}{4\tan{\frac{\pi}{n}}} \)
Tüm düzgün çokgenlerin çevrel çemberi de vardır ve merkezi düzgün çokgenin merkezi ile aynı noktadır. Bir düzgün çokgenin çevrel çemberinin yarıçap uzunluğu, çokgenin merkezinden herhangi bir köşesine çizilen doğru parçasının uzunluğuna eşittir.
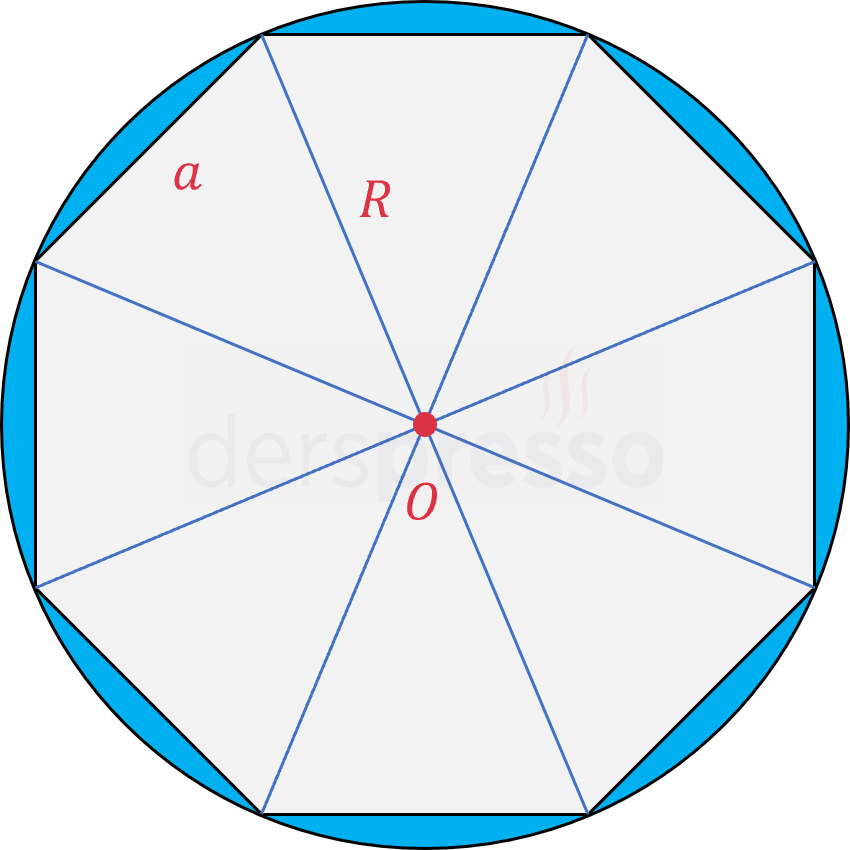
Bir kenar uzunluğu \( a \) olan \( n \) kenarlı düzgün çokgenin çevrel çemberinin yarıçapı (\( R \)) ve düzgün çokgenin alanı aşağıdaki formüllerle bulunabilir.
\( R = \dfrac{a}{2\sin{\frac{\pi}{n}}} \)
\( A = \dfrac{na^2}{4\tan{\frac{\pi}{n}}} \)
İSPATI GÖSTER
\( n \) kenarlı bir düzgün çokgenin merkezinden ardışık iki köşesine çizilen \( [OA] \) ve \( [OB] \) doğru parçaları şekildeki \( OAB \) ikizkenar üçgenini oluşturur.
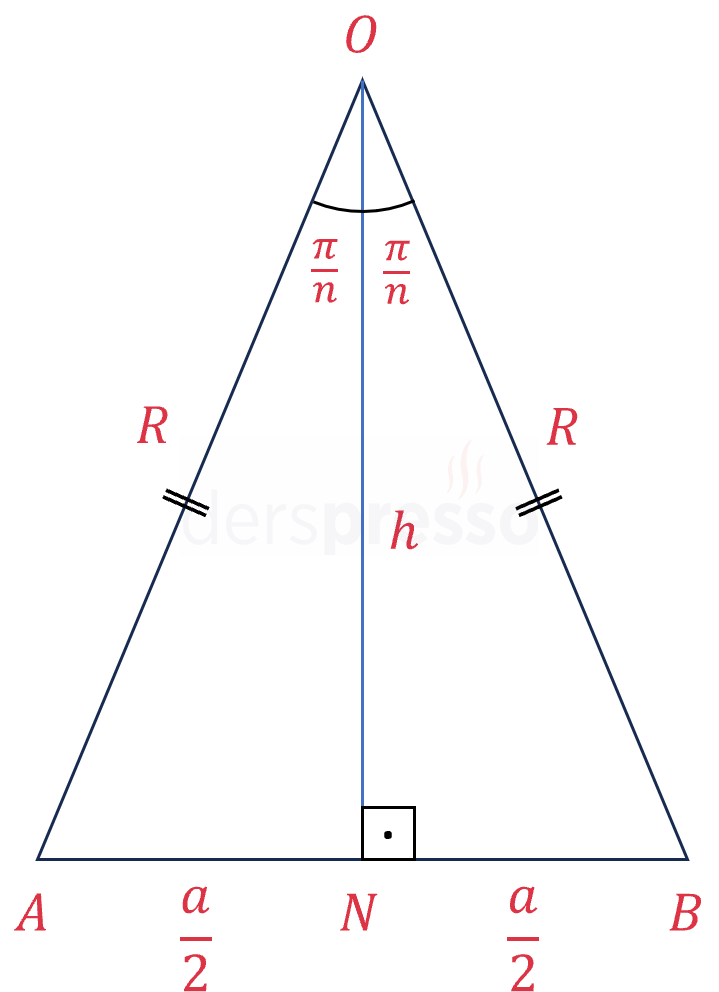
Düzgün çokgen bu üçgen ile eş \( n \) üçgenin biraraya gelmesiyle oluşur.
Üçgenin yan kenarları düzgün çokgenin çevrel çemberinin yarıçapına eşittir.
\( \abs{OA} = \abs{OB} = R \)
Üçgenin tepe açısını bulalım.
\( m(\widehat{AOB}) = \dfrac{360°}{n} = \dfrac{2\pi}{n} \)
\( m(\widehat{AON}) = m(\widehat{NOB}) = \dfrac{\pi}{n} \)
İkizkenar üçgende yükseklik tabanı ortalar.
\( \abs{AN} = \abs{NB} = \dfrac{a}{2} \)
Trigonometrik oranları kullanarak çevrel çemberin yarıçapını bulalım.
\( \sin{\frac{\pi}{n}} = \dfrac{\frac{a}{2}}{R} \)
\( R = \dfrac{a}{2\sin{\frac{\pi}{n}}} \)
Trigonometrik oranları kullanarak üçgenin yüksekliğini bulalım.
\( \tan{\frac{\pi}{n}} = \dfrac{\frac{a}{2}}{h} \)
\( h = \dfrac{a}{2\tan{\frac{\pi}{n}}} \)
Bu yükseklik değerini kullanarak düzgün çokgenin alanını bulalım.
Düzgün çokgenin alanı \( OAB \) üçgeninin alanının \( n \) katına eşittir.
\( A = n \cdot \dfrac{a \cdot h}{2} \)
\( h \) değerini yerine koyalım.
\( A = \dfrac{na \cdot \frac{a}{2\tan{\frac{\pi}{n}}}}{2} \)
\( A = \dfrac{na^2}{4\tan{\frac{\pi}{n}}} \)
Bir düzgün çokgenin merkezinden çizilen ve \( k \) kenarı gören açının ölçüsü çokgenin bir dış açısının \( k \) katına eşittir.
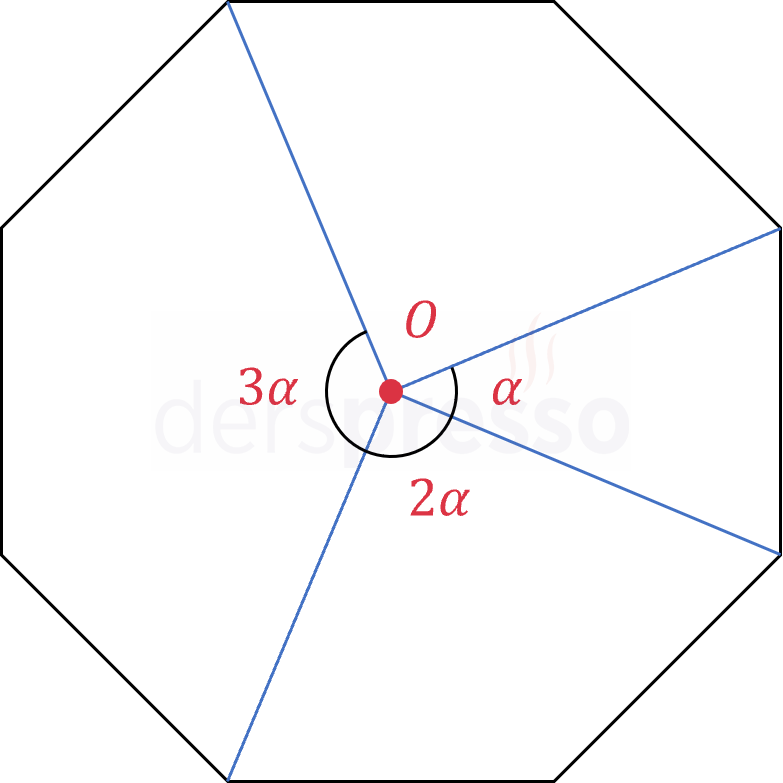
\( \alpha \) düzgün çokgenin bir dış açısı olmak üzere,
\( \alpha = \dfrac{360°}{n} \)
\( k \) kenarı gören merkez açının ölçüsü \( k\alpha \) olur.
İSPATI GÖSTER
\( n \) kenarlı bir düzgün çokgenin çevrel çemberini çizelim.
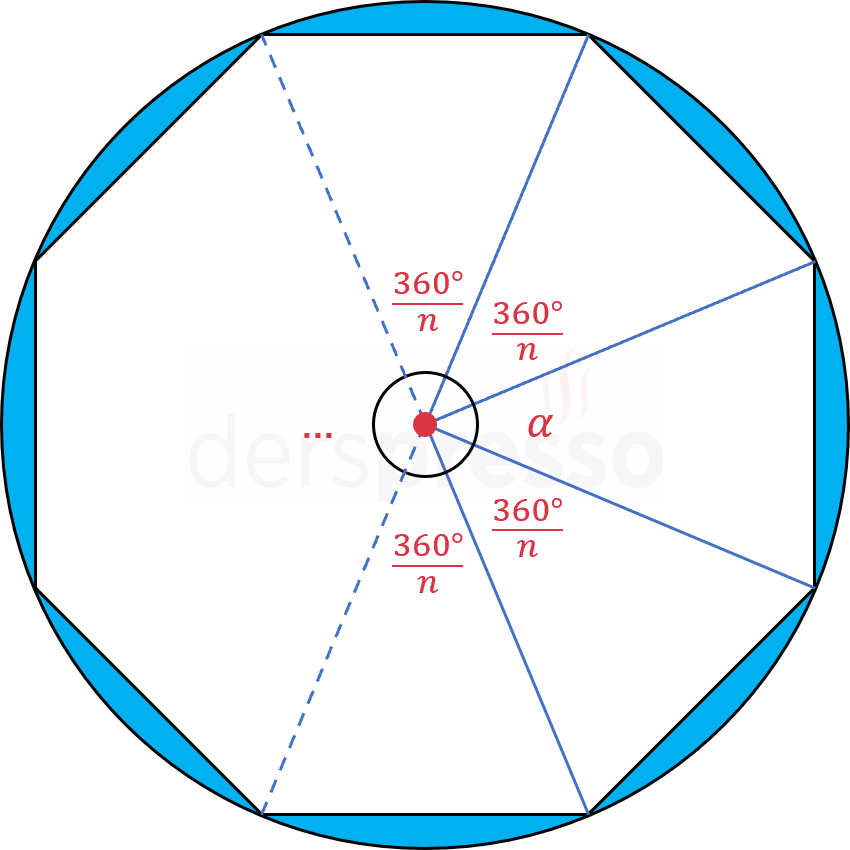
Düzgün çokgenin kenarları çevrel çemberin birer kirişidir.
Bir çemberde eşit uzunluktaki kirişler eşit uzunlukta yayları görürler. Buna göre düzgün çokgenin \( n \) kenarı çevrel çemberi her birinin ölçüsü \( \frac{360°}{n} \) olan \( n \) eşit yaya böler.
Bir çemberde merkez açı gördüğü yayın ölçüsüne eşittir.
\( \alpha = \dfrac{360°}{n} \)
Bu açı aynı zamanda düzgün çokgenin bir dış açısına eşittir.
Her bir kenarı gören merkez açı aynı \( \alpha \) derecelik yayı gördüğü için, \( k \) sayıda kenarı gören merkez açının ölçüsü düzgün çokgenin bir dış açının \( k \) katı olur.
Bir düzgün çokgenin herhangi bir köşesinden çizilen ve \( k \) kenarı gören açının ölçüsü çokgenin bir dış açısının \( k \) katının yarısına eşittir.
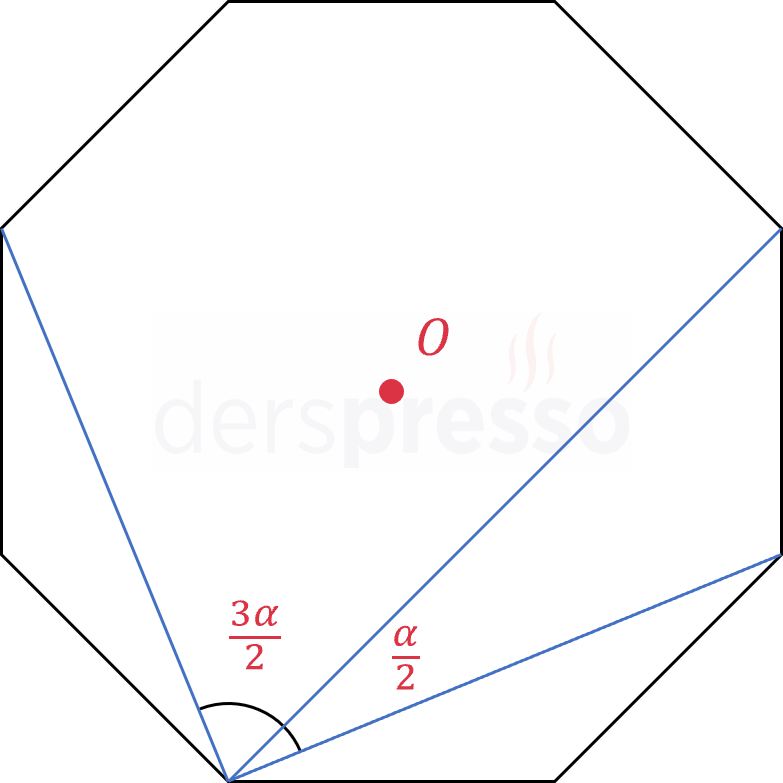
\( \alpha \) düzgün çokgenin bir dış açısı olmak üzere,
\( \alpha = \dfrac{360°}{n} \)
\( k \) kenarı gören çevre açısının ölçüsü \( \dfrac{k\alpha}{2} \) olur.
Bir çemberde bir yayı gören çevre açısının aynı yayı gören merkez açının yarısı olduğu bilgisi ve yukarıdaki merkez açı ispatı kullanılarak bu kuralın ispatı yapılabilir.
Bir dış açısı tam sayı olan kaç farklı düzgün çokgen çizilebilir?
Çözümü GösterDüzgün \( n \)-kenarlı çokgenin bir dış açısı aşağıdaki formülle hesaplanır.
Dış açı \( = \dfrac{360°}{n} \)
Bir dış açının tam sayı olabilmesi için \( \frac{360°}{n} \) ifadesi tam sayı olmalıdır, yani \( n \) 360'ın bir tam böleni olmalıdır.
360 sayısının kaç adet pozitif böleni olduğunu bulmak için asal çarpanlarına ayıralım ve bölen sayısı formülünü kullanalım.
\( 360 = 2^3 \cdot 3^2 \cdot 5^1 \)
Pozitif bölen sayısı asal çarpanların üslerinin birer fazlasının çarpımına eşittir.
\( (3 + 1)(2 + 1)(1 + 1) = 24 \)
360 sayısının 24 adet pozitif böleni vardır, ancak \( n = 1 \) ve \( n = 2 \) için birer düzgün çokgen oluşmaz.
Buna göre bir dış açısı tam sayı olan \( 24 - 2 = 22 \) adet düzgün çokgen çizilebilir.
Yarıçapı 6 cm olan bir çemberin üzerindeki birbirine eşit uzaklıktaki 12 noktanın birleştirilmesi ile oluşturulan düzgün onikigenin alanı nedir?
Çözümü GösterOnikigenin her bir köşesine çemberin merkezinden birer doğru çizelim.
Bu doğruların her biri yarıçaptır ve 6 cm uzunluğundadır. Bu yüzden çember ve onikigen 12 eşit parçaya ayrılır.
Doğrular arasında oluşan merkez açılar \( 360° \div 12 = 30° \) olur.
Onikigen tepe açısı 30° olan 12 eş ikizkenar üçgene bölünmüş olur.
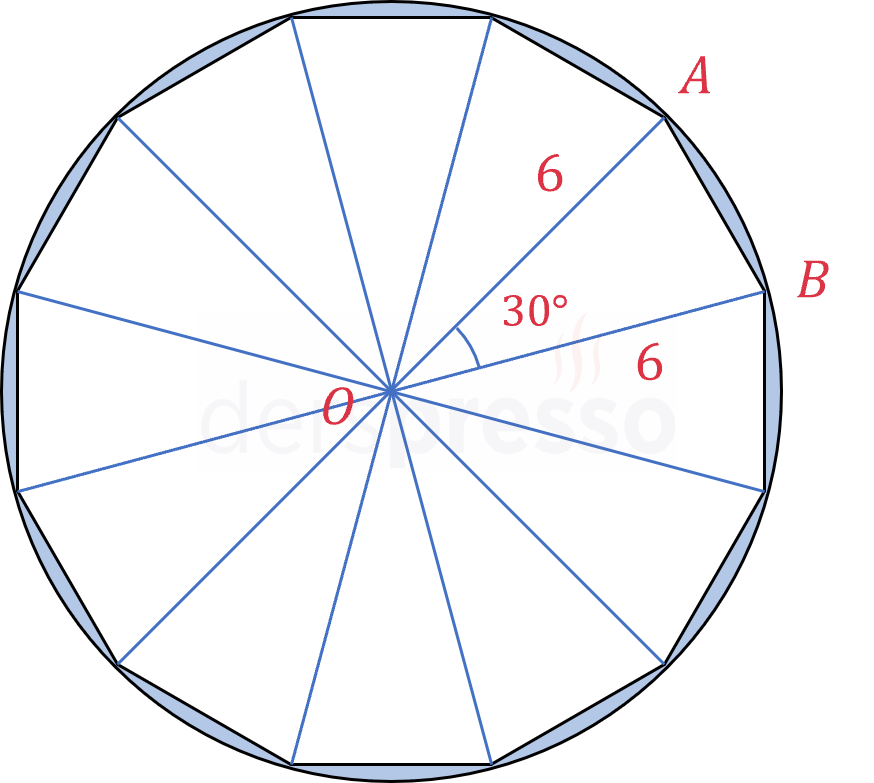
Sinüs alan teoremi ile bir üçgenin alanını bulalım.
\( A(OAB) = \dfrac{1}{2} \cdot [OA] \cdot [OB] \cdot \sin{30°} \)
\( = \dfrac{1}{2} \cdot 6 \cdot 6 \cdot \sin{30°} = 9 \)
Onikigenin alanı bir üçgenin alanının 12 katıdır.
\( A = 12 \cdot 9 = 108 \) bulunur.
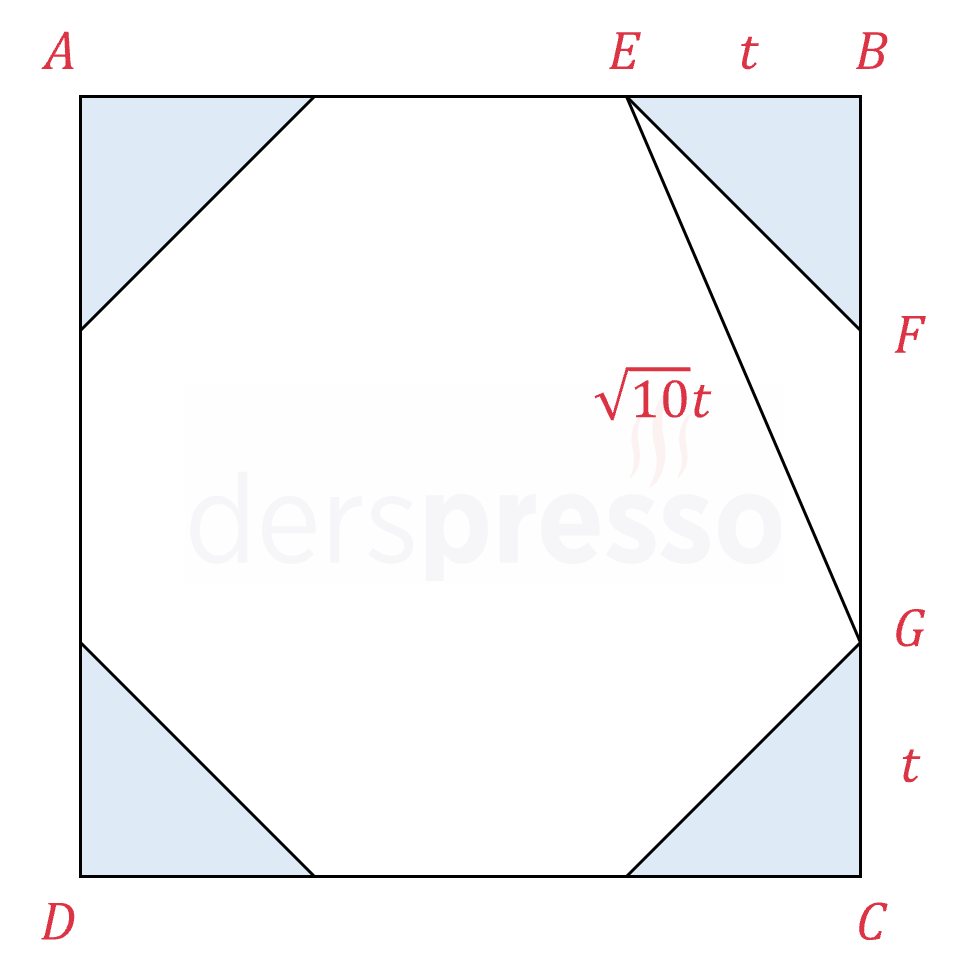
Yukarıda verilen bir kenar uzunluğu 12 birim olan karenin içinde bulunan sekizgenin tüm kenarları eşit uzunluktadır.
\( \abs{EB} = \abs{GC} = t, \quad \abs{EG} = \sqrt{10}t \) olduğuna göre, sekizgenin bir kenar uzunluğu kaçtır?
Çözümü GösterVerilen uzunluklardan ve Pisagor teoreminden yararlanarak eşitlikler kuralım.
\( [GC] = t \Longrightarrow [BG] = 12 - t \)
\( EBG \) dik üçgeninde Pisagor teoremini uygulayalım.
\( t^2 + (12 - t)^2 = (\sqrt{10}t)^2 \)
\( t^2 + 144 - 24t + t^2 = 10t^2 \)
\( 8t^2 + 24t - 144 = 0 \)
\( t^2 + 3t - 18 = 0 \)
\( (t + 6)(t - 3) = 0 \)
\( t \) negatif olamayacağı için \( t = 3 \) olur.
Sekizgenin bir kenar uzunluğuna \( p \) diyelim.
\( \abs{EF} = \abs{FG} = p \)
\( \abs{GC} = t = 3 \)
\( \abs{BI} = 12 - 3 - p = 9 - p \)
\( EBF \) dik üçgeninde Pisagor teoremini uygulayalım.
\( 3^2 + (9 - p)^2 = p^2 \)
\( 9 + 81 - 18p + p^2 = p^2 \)
\( 90 = 18p \)
\( p = 5 \) olarak bulunur.
Elde ettiğimiz kenar uzunluklarına dikkat edilirse; verilen sekizgen, eşkenar olan ama eş açılı olmayan, dolayısıyla düzgün olmayan bir sekizgendir.
Yüksekliği \( 9\sqrt{3} \) cm olan bir eşkenar üçgenle alanı eşit olan bir düzgün altıgenin bir kenar uzunluğu kaç santimetredir?
Çözümü GösterBir kenar uzunluğu \( a \) birim olan eşkenar üçgenin yüksekliği \( \dfrac{a\sqrt{3}}{2} \) birim olur.
Buna göre yüksekliği \( 9\sqrt{3} \) cm olan eşkenar üçgenin bir kenar uzunluğu \( 18 \) cm olur.
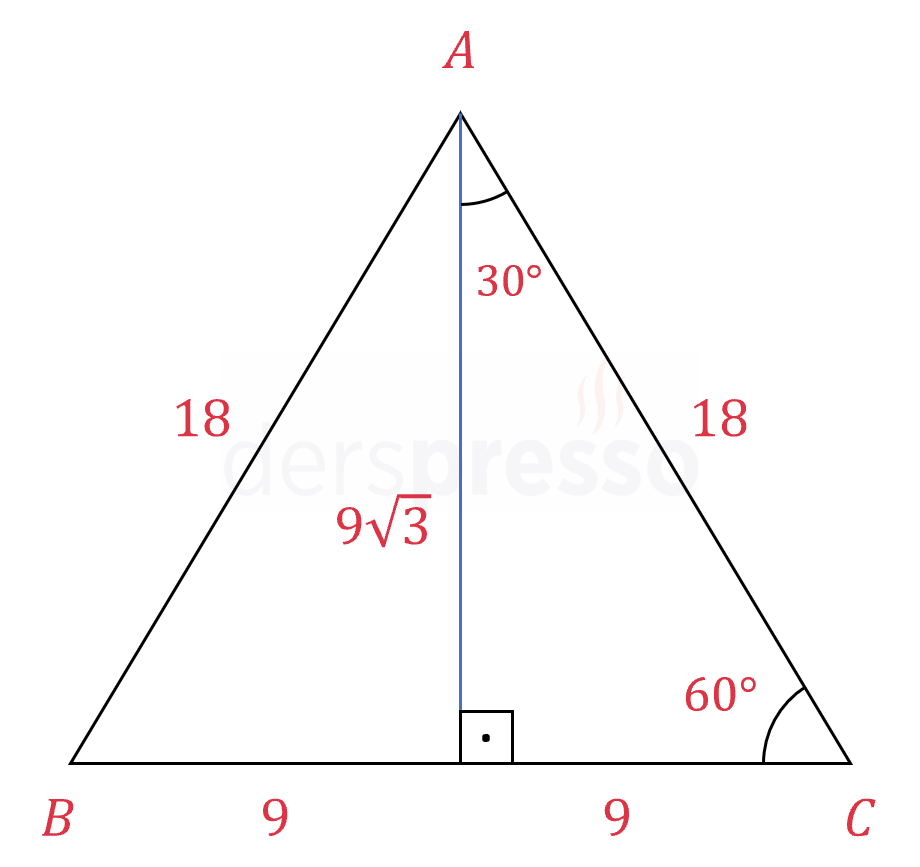
Bir kenar uzunluğu 18 cm olan eşkenar üçgenin alanını bulalım.
\( A_1 = \dfrac{a \cdot h}{2} \)
\( = \dfrac{18 \cdot 9\sqrt{3}}{2} = 81\sqrt{3} \)
Düzgün altıgenin bir kenarının uzunluğuna \( a \) diyelim.
Düzgün altıgen alanları birbirine eşit 6 eşkenar üçgenden oluşur.
Düzgün altıgeni oluşturan eşkenar üçgenlerden birinin alanını bulalım.
\( A_2 = \dfrac{a \cdot \frac{a\sqrt{3}}{2}}{2} = \dfrac{\sqrt{3}a^2}{4} \)
İki şeklin alanı birbirine eşittir.
\( A_1 = 6A_2 \)
\( 81\sqrt{3} = 6 \cdot \dfrac{\sqrt{3}a^2}{4} \)
\( a^2 = 54 \)
\( a = 3\sqrt{6} \)
Buna göre düzgün altıgenin bir kenar uzunluğu \( 3\sqrt{6} \) cm'dir.
Şekilde bir düzgün onikigen ve bu onikigenin içinde bir \( ABCD \) dikdörtgeni verilmiştir.
Buna göre dikdörtgenin alanının onikigenin alanına oranı kaçtır?
Çözümü GösterHem onikigenin hem de dikdörtgenin karşılıklı köşeleri arasında köşegenler çizelim.
Dikdörtgenin köşeleri onikigenin 4 köşesinde olduğundan tüm köşegenlerin kesişim noktası aynı \( O \) noktasıdır.
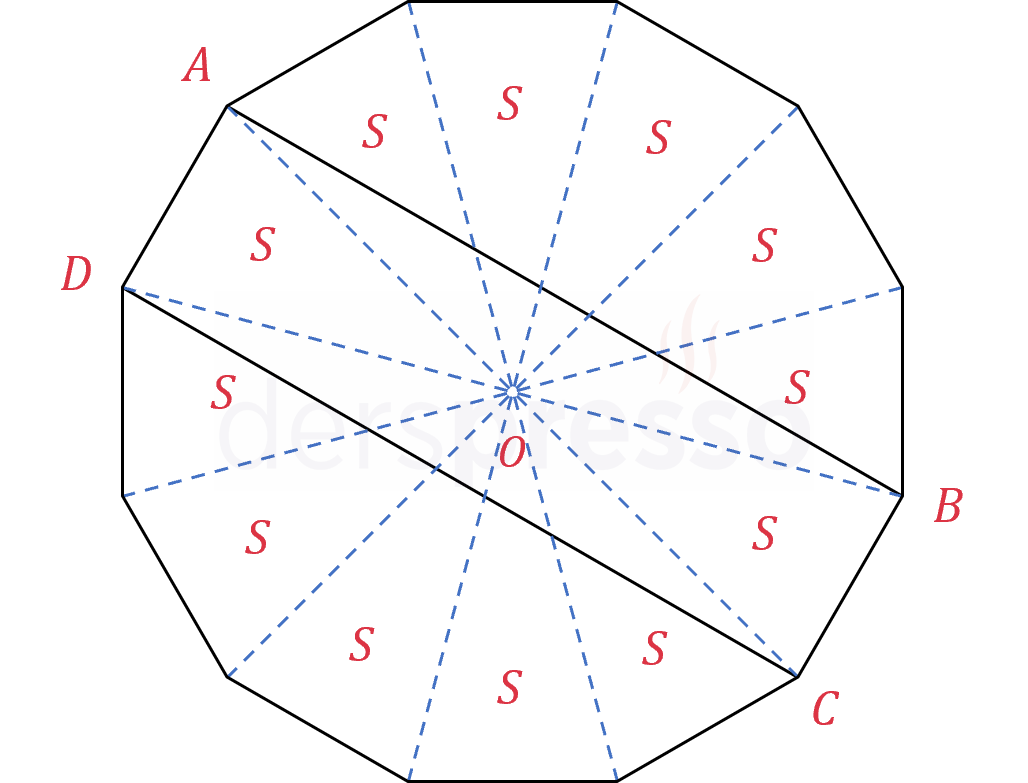
Çokgenin içinde oluşan 12 adet eş ikizkenar üçgenin her birinin alanına \( S \) diyelim.
Bir dikdörtgende köşegenlerin ayırdığı parçaların alanları eşittir. Bu durumda alan değerleri aşağıdaki gibi olur.
\( A(ADO) = A(AOB) = A(BOC) = A(COD) = S \)
Buna göre \( ABCD \) dikdörtgeninin alanı \( 4S \), düzgün onikigenin alanı \( 12S \) olur.
\( \dfrac{4S}{12S} = \dfrac{1}{3} \) bulunur.
Bir eşkenar üçgen ve bir düzgün altıgenin çevreleri birbirine eşittir. Buna göre üçgenin alanının altıgenin alanına oranı kaçtır?
Çözümü GösterBir kenar uzunluğu \( x \) olan eşkenar üçgenin alanı aşağıdaki formülle bulunur.
\( A = \dfrac{x^2 \sqrt{3}}{4} \)
Altıgen 6 adet eşkenar üçgenden oluştuğu için alanı bulunurken bu formül 6 ile çarpılır.
Üçgenin bir kenarına \( 2a \) diyelim.
Üçgenin çevresi \( 3 \cdot 2a = 6a \) olacağı için altıgenin bir kenar uzunluğu \( a \) olmalıdır.
Üçgenin alanının altıgenin alanına oranını bulalım.
\( \dfrac{\dfrac{(2a)^2 \sqrt{3}}{4}}{\dfrac{6a^2 \sqrt{3}}{4}} = \dfrac{4}{6} = \dfrac{2}{3} \) bulunur.
Soruyu formül kullanmadan da çözebiliriz.
Altıgeni oluşturan eşkenar üçgenlerin her biri ile soruda verilen eşkenar üçgen benzer üçgenler olup benzerlik oranı 2'dir.
Benzerlik oranının karesi alanların oranını verir. Yani altıgeni oluşturan eşkenar üçgenlerin birinin alanına \( S \) dersek büyük üçgenin alanı \( 4S \) olur.
\( \dfrac{4S}{6 \cdot S} = \dfrac{2}{3} \) bulunur.
Yukarıdaki şekilde birer kenarı ortak olan bir düzgün beşgen ve kare verilmiştir.
Buna göre, \( x \) açısının ölçüsü kaçtır?
Çözümü GösterDüzgün beşgenin bir iç açısının ölçüsünü bulalım.
\( \dfrac{180 \cdot (5 - 2)}{5} = 108° \)
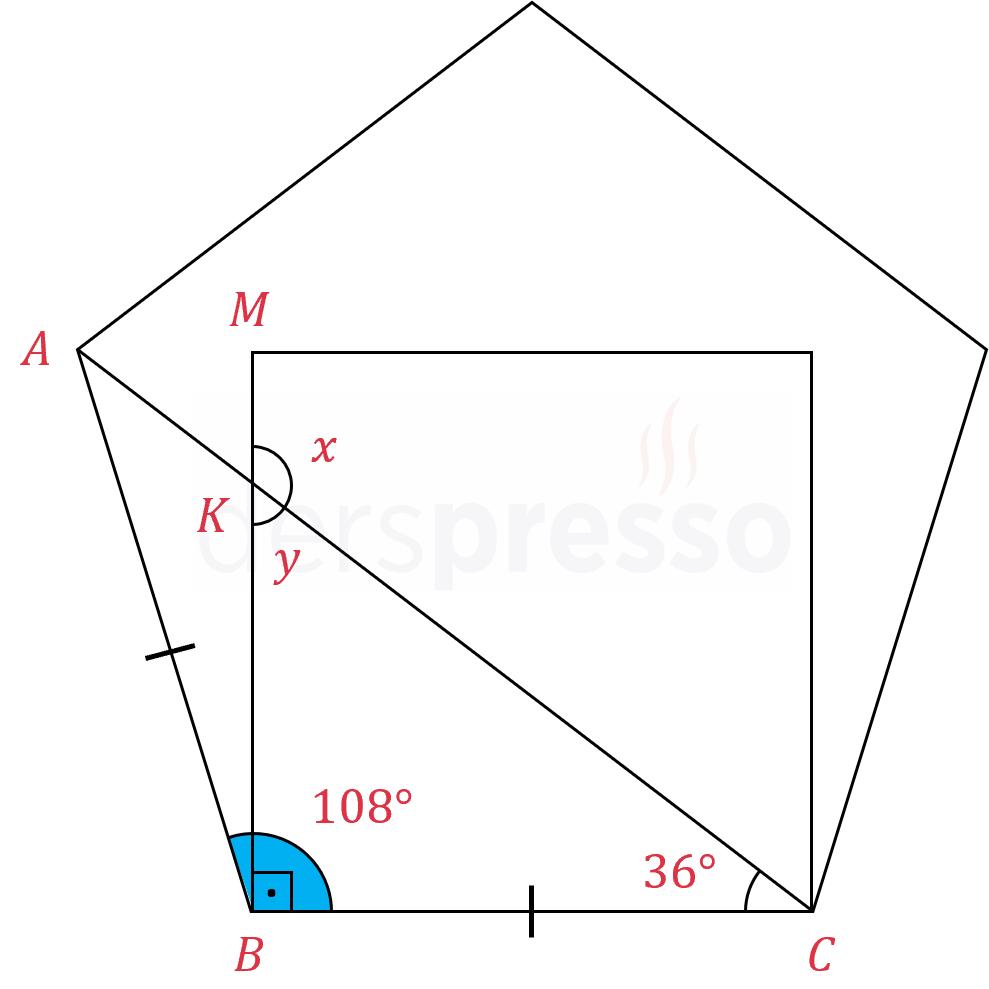
\( ABC \) üçgeninin iki kenarı düzgün beşgen üzerinde olduğu için bir ikizkenar üçgendir.
\( m(\widehat{ACB}) = \dfrac{180 - 108}{2} = 36° \)
\( KBC \) dik üçgeninin iç açıları toplamı 180°'dir.
\( 90 + 36 + y = 180 \)
\( y = 54° \)
\( x \) ve \( y \) bütünler açılardır.
\( x = 180 - 54 = 126° \) bulunur.
Yapılan arkeolojik kazılarda iki eski medeniyetin açıları sırasıyla "daryan" ve "cerede" birimleri ile ifade ettikleri ve 1 daryanın 4 ceredeye eşit olduğu görülüyor.
Düzgün ongenin bir iç açısı 6 daryan ise bir dış açısı kaç cerededir?
Çözümü GösterDaryanın ölçü birimine \( d \), ceredenin ölçü birimine \( c \) diyelim.
Ongenin derece cinsinden bir iç açısı: \( \dfrac{(10 - 2) \cdot 180}{10} = 8 \cdot 18 \)
Bu açı 6 daryana eşittir.
\( 8 \cdot 18 = 6d \)
\( d = 24° \)
1 daryan 4 ceredeye eşittir.
\( d = 4c = 24° \Longrightarrow c = 6° \)
Düzgün ongenin bir dış açısı: \( \dfrac{360}{10} = 36° \)
Bu açının kaç ceredeye eşit olduğunu bulalım.
1 cerede 6° ise \( x \) cerede 36°'dir.
\( 36° = 6c \)
Düzgün ongenin bir dış açısı 6 cerede olur.
İç açıları tam sayı olan kaç farklı düzgün çokgen vardır?
Çözümü GösterBir düzgün çokgenin bir iç açısı tam sayı ise bir dış açısı da tam sayıdır.
Bir çokgenin dış açıları toplamı 360 derecedir.
360'ın her bir pozitif bölenine bölümünde elde edilen sonuç, farklı bir tam sayı dış açı değerini verir.
360'ın toplam pozitif bölen sayısını bulalım.
\( 360 = 2^3 \cdot 3^2 \cdot 5 \)
Buna göre 360'ın toplam \( (3 + 1)(2 + 1)(1 + 1) = 24 \) tane pozitif böleni vardır.
1 ve 2 kenarlı düzgün çokgen olmadığı için bu iki durumu 24'ten çıkaralım.
\( 24 - 2 = 22 \) bulunur.
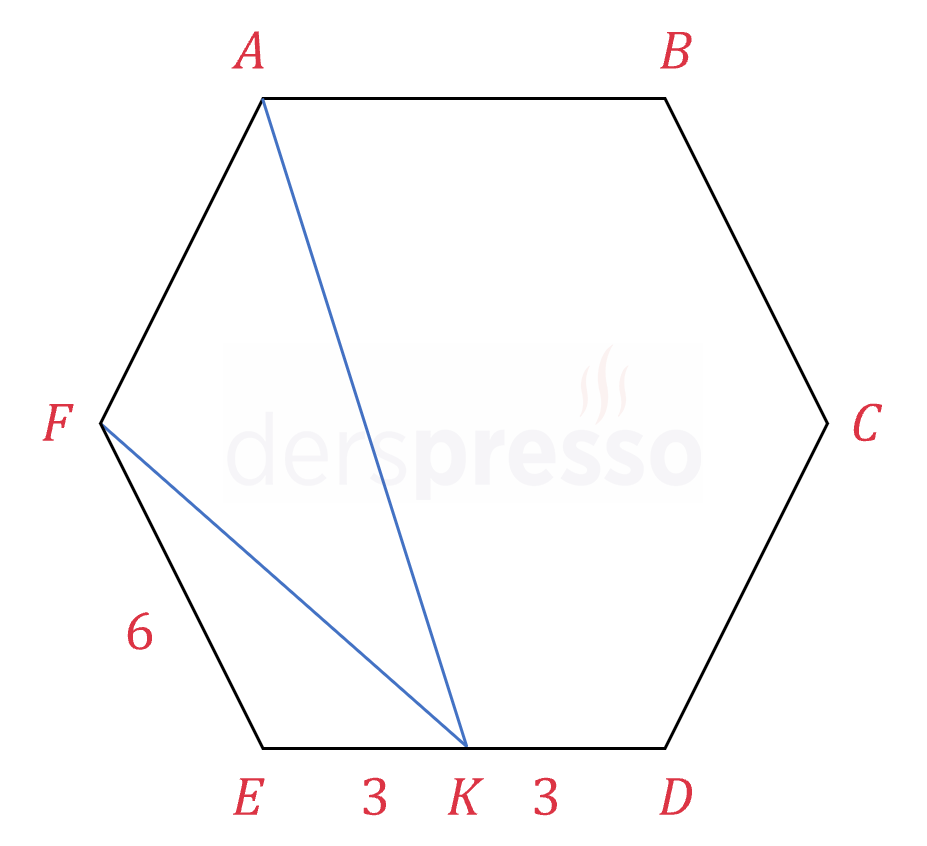
\( ABCDEF \) bir kenarı 6 cm olan bir düzgün altıgendir.
\( K \), \( [ED] \) kenarının orta noktasıdır.
Buna göre \( \abs{FK} + \abs{AK} \) kaç cm'dir?
Çözümü Göster\( n \) kenarı olan düzgün bir çokgenin bir iç açısı \( \frac{(n - 2)}{n} \cdot 180° \) formülü ile bulunur.
Buna göre düzgün altıgenin bir iç açısı 120°'dir.
\( \dfrac{(6 - 2)}{6} \cdot 180° = 120° \)
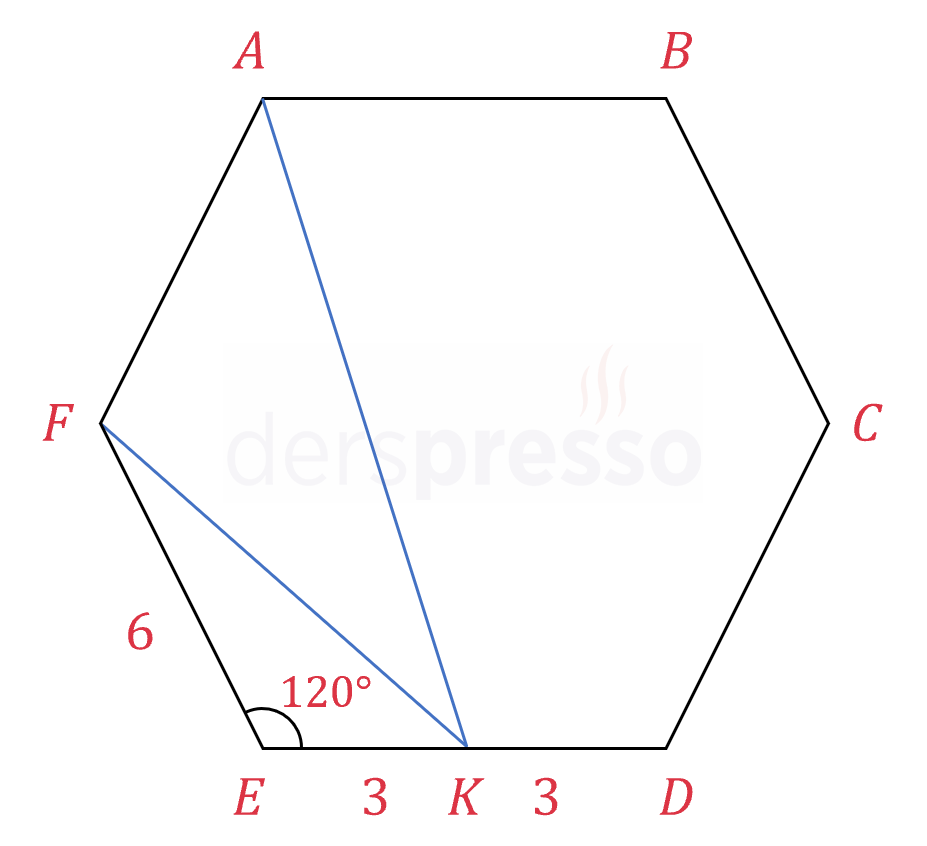
\( FEK \) üçgenine kosinüs teoremini uygulayarak \( \abs{FK} \) uzunluğunu bulalım.
\( \abs{FK}^2 = 6^2 + 3^2 - 2 \cdot 6 \cdot 3 \cdot \cos{120°} \)
\( = 36 + 9 - 36 \cdot \dfrac{-1}{2} = 63 \)
\( \abs{FK} = 3\sqrt{7} \)
\( \abs{AK} \) uzunluğunu bulmak için \( A \) ve \( E \) noktalarını birleştiren bir doğru parçası çizelim.
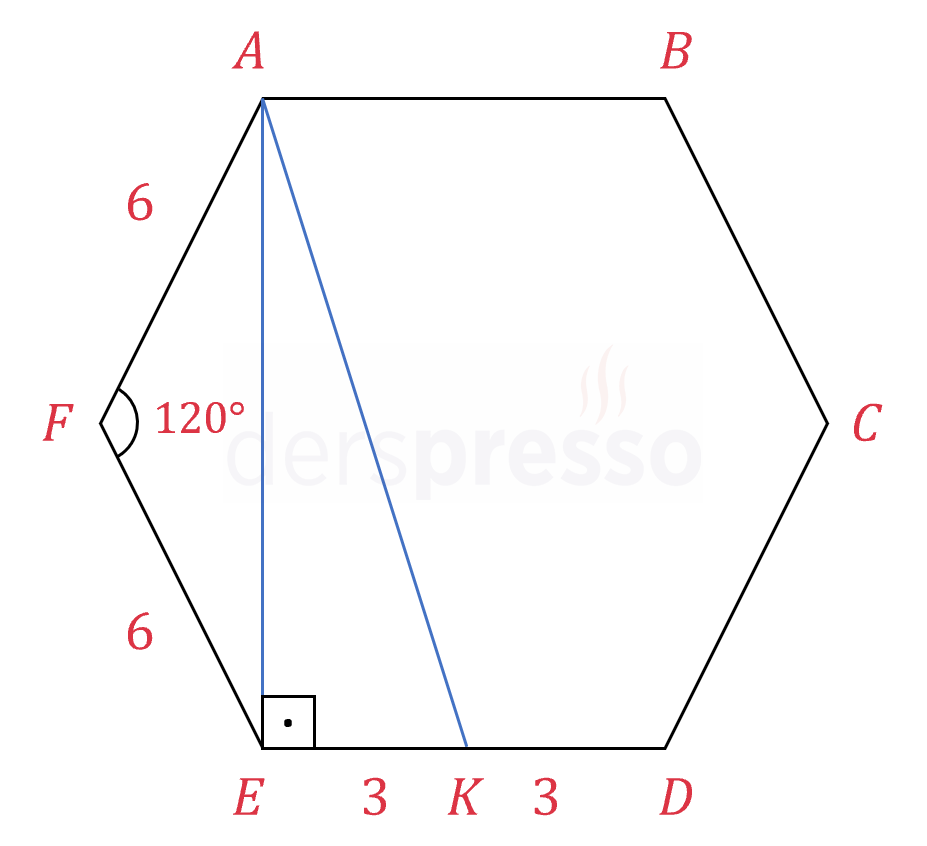
\( AFE \), tepe açısı 120° olan bir ikizkenar üçgendir. Buna göre taban açıları \( \frac{180 - 120}{2} = 30° \) olur.
\( AFE \) üçgeni 120 - 30 - 30° üçgeni olduğundan 120°'yi gören kenar olan \( AE \) kenarı \( 6\sqrt{3} \) cm'dir.
\( m(\widehat{FED}) = 120° \) ve \( m(\widehat{FEA}) = 30° \) olduğuna göre, \( m(\widehat{AEK}) = 120 - 30 = 90° \) bulunur.
\( \abs{AK} \) uzunluğunu \( AEK \) üçgeninde Pisagor teoremini kullanarak bulalım.
\( \abs{AK}^2 = (6\sqrt{3})^2 + 3^2 \)
\( = 108 + 9 = 117 \)
\( \abs{AK} = 3\sqrt{13} \) bulunur.
\( \abs{FK} + \abs{AK} = 3\sqrt{7} + 3\sqrt{13} \) cm bulunur.
Kenarları 5 cm olan bir kare köşelerinden kesilerek bir düzgün sekizgen oluşturuluyor.
Bu düzgün sekizgenin çevresi kaç cm'dir?
Çözümü GösterSekizgenin bir kenar uzunluğuna \( a \) diyelim.
Bir çokgenin dış açıları toplamı 360°'dir.
Buna göre karenin köşelerinden kesilen üçgenlerin dar açıları \( \frac{360}{8} = 45° \) olarak bulunur.
Sekizgenin tüm dış açıları 45° olduğu için, karenin köşelerinden kesilen üçgenler ikizkenar olup dik kenar uzunlukları \( \frac{5 - a}{2} \) olur.
Pisagor teoremine göre, 45-45-90 dik üçgeninde hipotenüs uzunluğu dik kenar uzunluğunun \( \sqrt{2} \) katına eşittir.
\( a = \dfrac{5 - a}{2} \cdot \sqrt{2} \)
\( \sqrt{2}a = 5 - a \)
\( a \)'yı yalnız bırakalım.
\( \sqrt{2}a + a = 5 \)
\( a = \dfrac{5}{\sqrt{2} + 1} \)
Düzgün sekizgenin çevre uzunluğunu bulalım.
\( 8a = 8 \cdot \dfrac{5}{\sqrt{2} + 1} = \dfrac{40}{\sqrt{2} + 1} \)
Paydayı rasyonel hale getirelim.
\( = \dfrac{40(\sqrt{2} - 1)}{(\sqrt{2} + 1)(\sqrt{2} - 1)} \)
\( = 40(\sqrt{2} - 1) \) bulunur.
İç açılarının ondalık kısmı 0,5 olan (örneğin 4,5) kaç farklı düzgün çokgen vardır?
Çözümü GösterBir iç açının ondalık kısmı 0,5 olduğunda bir dış açının ondalık kısmı da 0,5 olur.
\( n \) kenarlı bir düzgün çokgenin dış açıları toplamı 360°' dir.
Bir düzgün çokgende \( \frac{720}{n} \) ifadesinin tam sayı olması durumunda çokgenin bir iç açısı 0,5'in bir tam sayı katı olur.
\( \frac{360}{n} \) ifadesinin tam sayı olması durumunda ise çokgenin bir iç açısı tam sayı olur.
Dolayısıyla \( \frac{720}{n} \) ifadesini tam sayı yapan \( n \) değerlerinden \( \frac{360}{n} \) ifadesini tam sayı yapan \( n \) değerlerini çıkardığımızda ondalık kısmı 0,5 olan düzgün çokgenlerin kenar sayılarını buluruz.
720'nin pozitif bölen sayısını bulalım.
\( 720 = 2^4 \cdot 3^2 \cdot 5 \)
Buna göre 720 sayısının \( (4 + 1)(2 + 1)(1 + 1) = 30 \) pozitif tam böleni vardır.
\( n = 1 \) ve \( n = 2 \) değerleri için bir çokgen oluşmayacağı için bir iç açısı 0,5'in bir tam sayı katı olan 28 düzgün çokgen vardır.
360'ın pozitif bölen sayısını bulalım.
\( 360 = 2^3 \cdot 3^2 \cdot 5 \)
Buna göre 360 sayısının \( (3 + 1)(2 + 1)(1 + 1) = 24 \) pozitif tam böleni vardır.
\( n = 1 \) ve \( n = 2 \) değerleri için bir çokgen oluşmayacağı için bir iç açısı tam sayı olan 22 düzgün çokgen vardır.
Buna göre, açılarının ondalık kısmı 0,5 olan \( 28 - 22 = 6 \) düzgün çokgen vardır.