Kutupsal Denklem Örnekleri
Bu bölümde en sık karşımıza çıkabilecek kutupsal denklem tiplerini ve grafiklerini inceleyeceğiz.
Doğru
Doğrunun kutupsal denklemi aşağıdaki gibidir.
Doğrunun kartezyen denklemi:
\( ax + by = c \)
Doğrunun kutupsal denklemi:
\( r = \dfrac{c}{a\cos{\theta} + b\sin{\theta}} \)
Kartezyen denklemi:
\( 2x - 3y = 6 \)
Kutupsal denklem:
\( r = \dfrac{6}{2\cos{\theta} - 3\sin{\theta}} \)
İSPATI GÖSTER
Doğrunun denklemini yazalım.
\( ax + by = c \)
\( x \) ve \( y \) koordinatlarının kutupsal koordinat karşılıklarını yazalım.
\( x = r\cos{\theta} \)
\( y = r\sin{\theta} \)
Bu değerleri doğrunun denkleminde yerine koyalım.
\( a(r\cos{\theta}) + b(r\sin{\theta}) = c \)
\( ar\cos{\theta} + br\sin{\theta} = c \)
Eşitliğin sol tarafını \( r \) parantezine alalım.
\( r(a\cos{\theta} + b\sin{\theta}) = c \)
\( r \)'yi yalnız bıraktığımızda doğrunun kutupsal denklemini elde ederiz.
\( r = \dfrac{c}{a\cos{\theta} + b\sin{\theta}} \)
Aşağıda farklı doğruların kartezyen ve kutupsal denklemleri ve grafikleri verilmiştir.
| Grafik | Denklem |
|---|---|
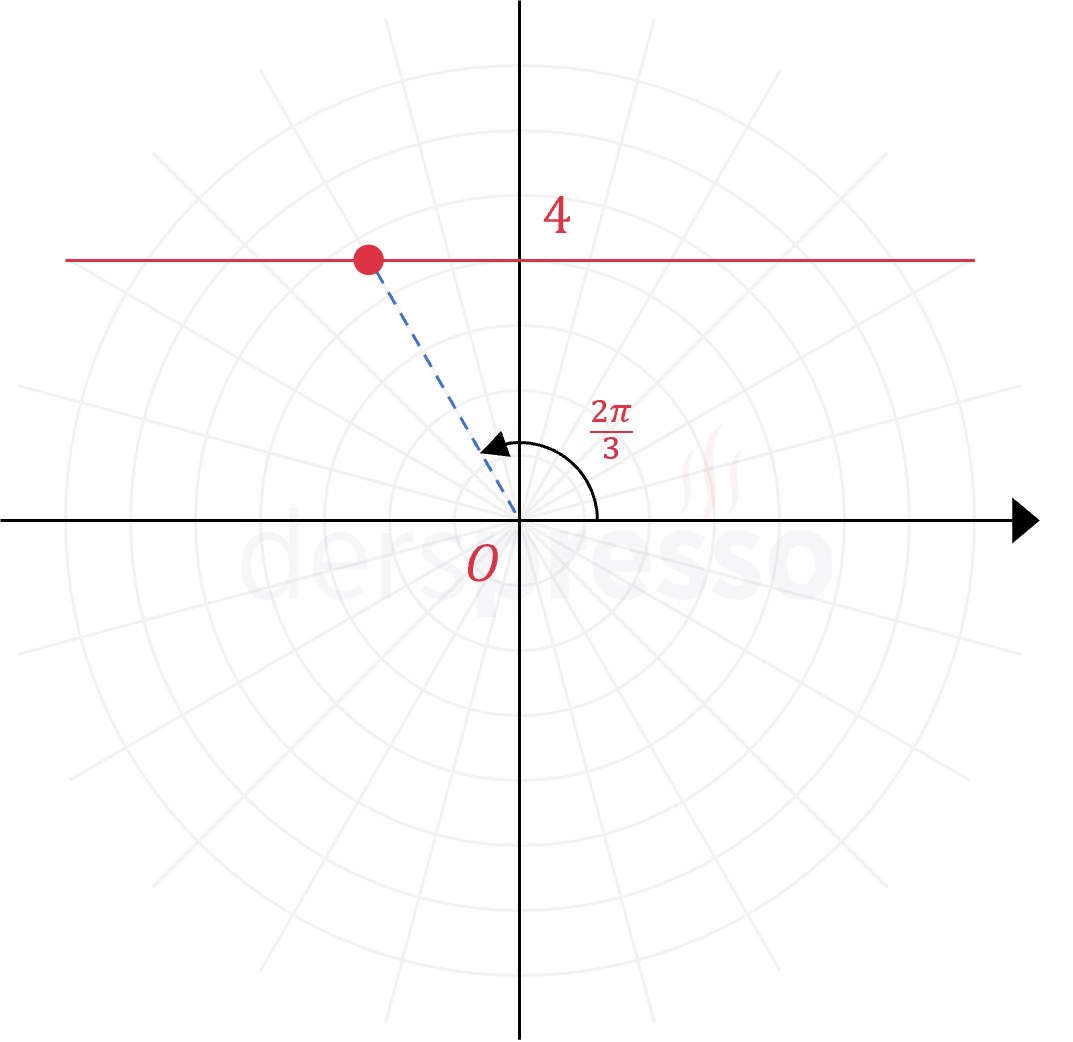
|
Yatay doğru Kartezyen denklemi: \( y = 4 \) Kutupsal denklem: \( r = \dfrac{4}{\sin{\theta}} \) Örnek denklem sadece sinüs fonksiyonu içerdiği için \( \theta = \frac{\pi}{2} \) doğrusuna göre simetriktir. Örnek nokta: \( r = \dfrac{4}{\sin{\frac{2\pi}{3}}} = \dfrac{8\sqrt{3}}{3} \) \( (r, \theta) = (\frac{8\sqrt{3}}{3}, \frac{2\pi}{3}) \) |
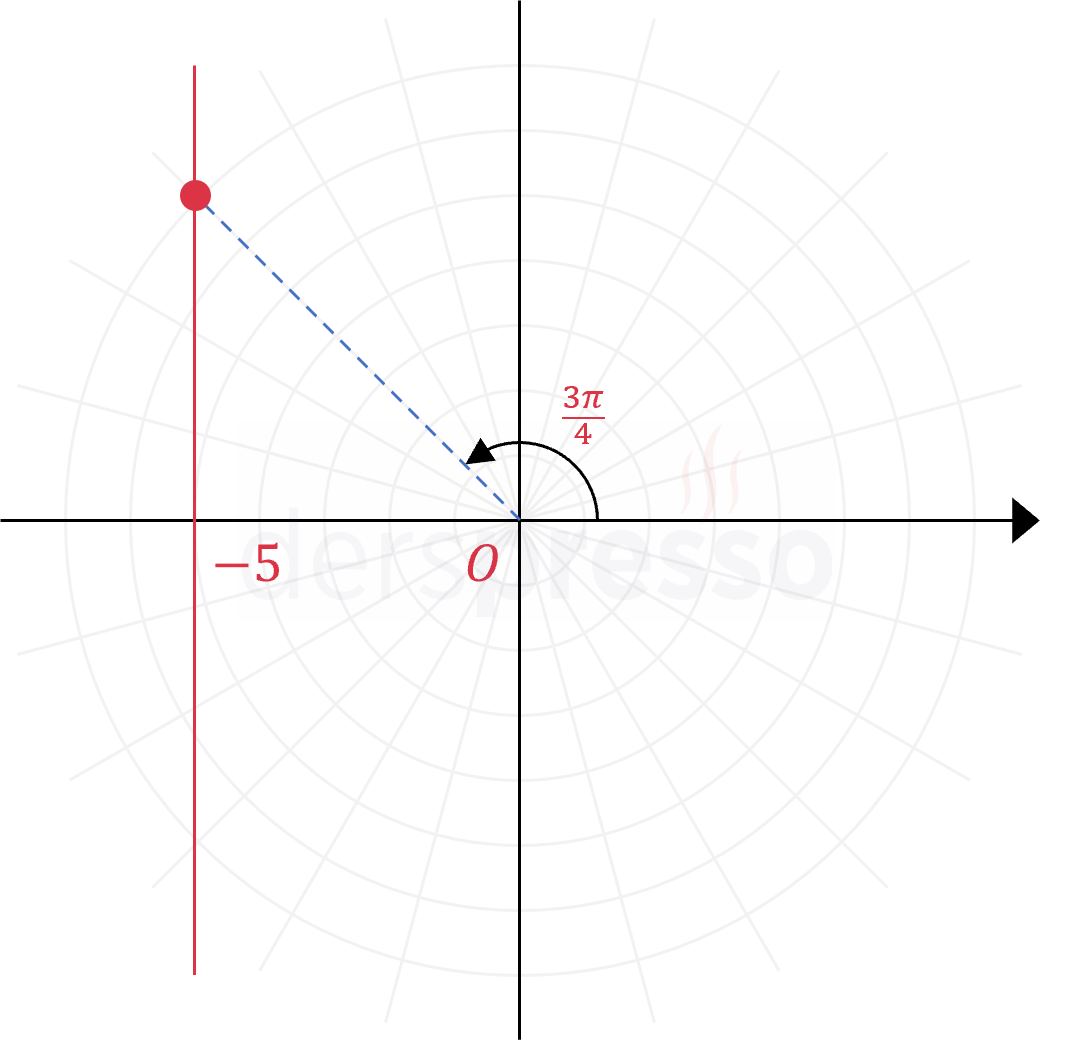
|
Dikey doğru Kartezyen denklemi: \( x = -5 \) Kutupsal denklem: \( r = \dfrac{-5}{\cos{\theta}} \) Örnek denklem sadece kosinüs fonksiyonu içerdiği için kutup eksenine göre simetriktir. Örnek nokta: \( r = \dfrac{-5}{\cos{\frac{3\pi}{4}}} = 5\sqrt{2} \) \( (r, \theta) = (5\sqrt{2}, \frac{3\pi}{4}) \) |

|
1. açıortay doğrusu Kartezyen denklemi: \( y = x \) Kutupsal denklem: \( \theta = \dfrac{\pi}{4} \) Örnek nokta: \( (r, \theta) = (-3, \frac{\pi}{4}) \) |

|
Orijinden geçen doğru Kartezyen denklemi: \( y = -\sqrt{3}x \) Kutupsal denklem: \( \theta = \dfrac{2\pi}{3} \) Örnek nokta: \( (r, \theta) = (-6, \frac{2\pi}{3}) \) |
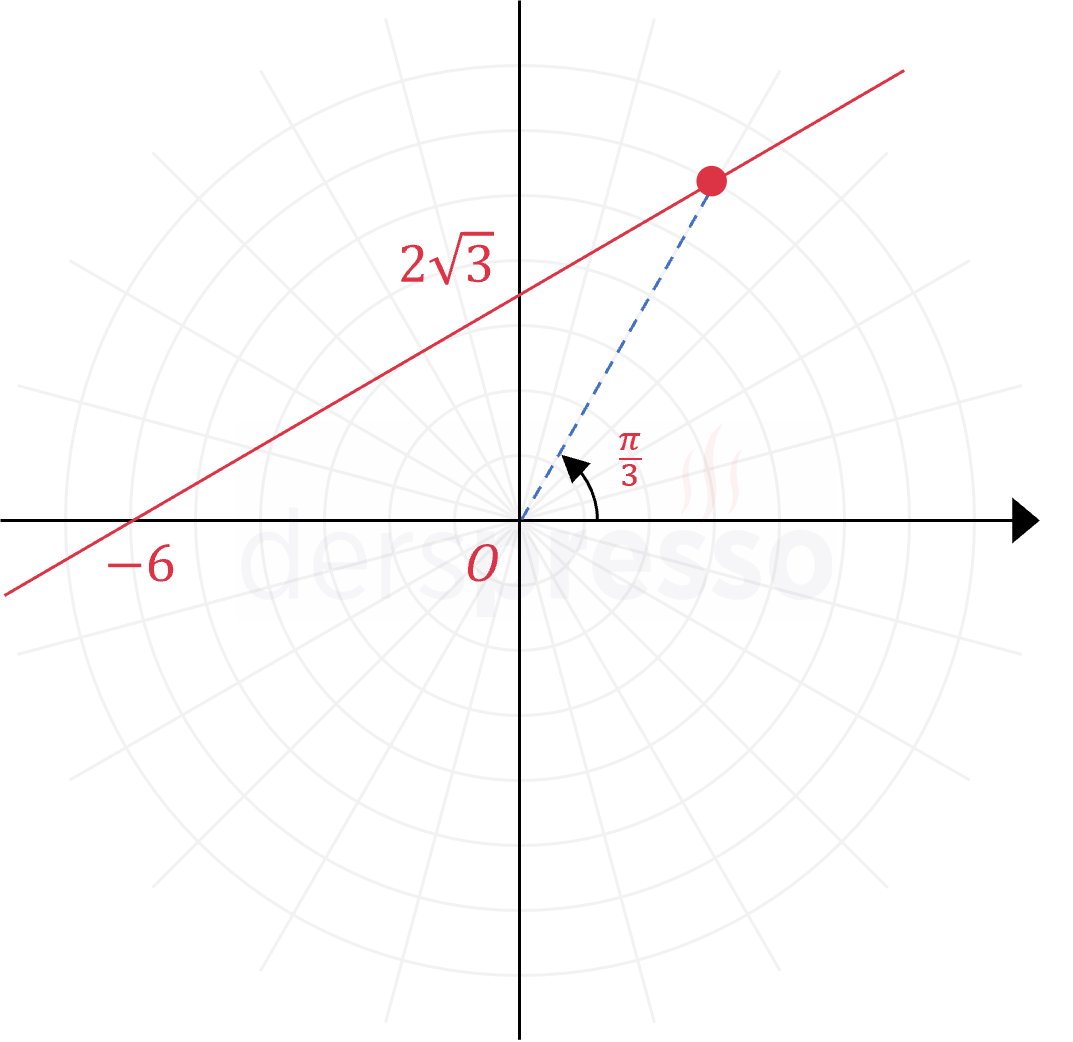
|
Doğru Kartezyen denklemi: \( x - \sqrt{3}y = -6 \) Kutupsal denklem: \( r = \dfrac{-6}{\cos{\theta} - \sqrt{3}\sin{\theta}} \) Örnek nokta: \( r = \dfrac{-6}{\cos{\frac{\pi}{3}} - \sqrt{3}\sin{\frac{\pi}{3}}} = 6 \) \( (r, \theta) = (6, \frac{\pi}{3}) \) |
Çember
Çemberin kutupsal denklemi aşağıdaki gibidir.
Merkezi \( (a, b) \) ve yarıçapı \( R \) olan çemberin kartezyen denklemi:
\( (x - a)^2 + (y - b)^2 = R^2 \)
Merkezi \( (r_0, \beta) \) ve yarıçapı \( R \) olan çemberin kutupsal denklemi:
\( r^2 + r_0^2 - 2rr_0\cos(\theta - \beta) = R^2 \)
Kartezyen denklemi:
\( (x - 5)^2 + y^2 = 5^2 \)
Kutupsal denklem:
\( r^2 + 5^2 - 2r(5)\cos(\theta - 0) = 5^2 \)
\( r = 10\cos{\theta} \)
İSPATI GÖSTER
Aşağıdaki şekilde merkezinin kutupsal koordinatları \( M(r_0, \beta) \) ve yarıçapı \( R \) olan çember verilmiştir.
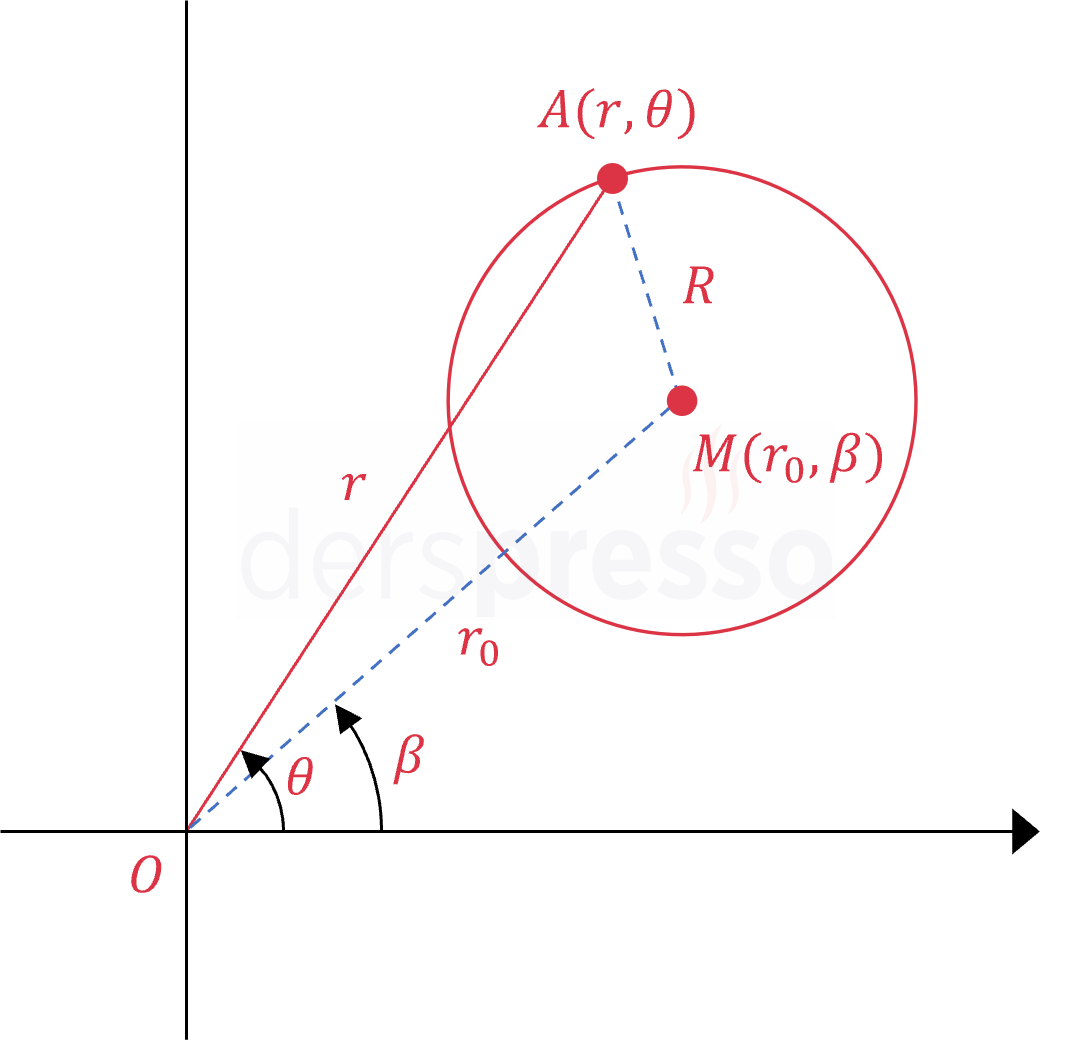
\( M \) noktasına uzaklığı \( R \) ve kutupsal koordinatları \( A(r, \theta) \) olan noktaların geometrik yer denklemini yazalım.
\( \abs{AM} = R \)
\( A \) noktasının kartezyen koordinatlarını yazalım.
\( (r, \theta) = (r\cos{\theta}, r\sin{\theta}) \)
\( M \) noktasının kartezyen koordinatlarını yazalım.
\( (r_0, \beta) = (r_0\cos{\beta}, r_0\sin{\beta}) \)
\( \abs{AM} \) uzaklığını bulalım.
\( \sqrt{(r\cos{\theta} - r_0\cos{\beta})^2 + (r\sin{\theta} - r_0\sin{\beta})^2} \)
\( = \sqrt{r^2\cos^2{\theta} - 2rr_0\cos{\theta}\cos{\beta} + r_0^2\cos^2{\beta} + r^2\sin^2{\theta} - 2rr_0\sin{\theta}\sin{\beta} + r_0^2\sin^2{\beta}} \)
\( = \sqrt{r^2(\cos^2{\theta} + \sin^2{\theta}) + r_0^2(\cos^2{\beta} + \sin^2{\beta}) - 2rr_0(\cos{\theta}\cos{\beta} + \sin{\theta}\sin{\beta})} \)
\( \sin{x} + \cos{x} = 1 \) özdeşliğini kullanalım.
\( = \sqrt{r^2 + r_0^2 - 2rr_0(\cos{\theta}\cos{\beta} + \sin{\theta}\sin{\beta})} \)
Kosinüs fark formülünü kullanalım.
\( \cos(x - y) = \cos{x}\cos{y} + \sin{x}\sin{y} \)
\( = \sqrt{r^2 + r_0^2 - 2rr_0\cos(\theta - \beta)} \)
Bu değer çemberin yarıçapına eşittir.
\( \sqrt{r^2 + r_0^2 - 2rr_0\cos(\theta - \beta)} = R \)
İki tarafın karesini aldığımızda çemberin kutupsal denklemini elde ederiz.
\( r^2 + r_0^2 - 2rr_0\cos(\theta - \beta) = R^2 \)
Aşağıda farklı çemberlerin kartezyen ve kutupsal denklemleri ve grafikleri verilmiştir.
| Grafik | Denklem |
|---|---|
|
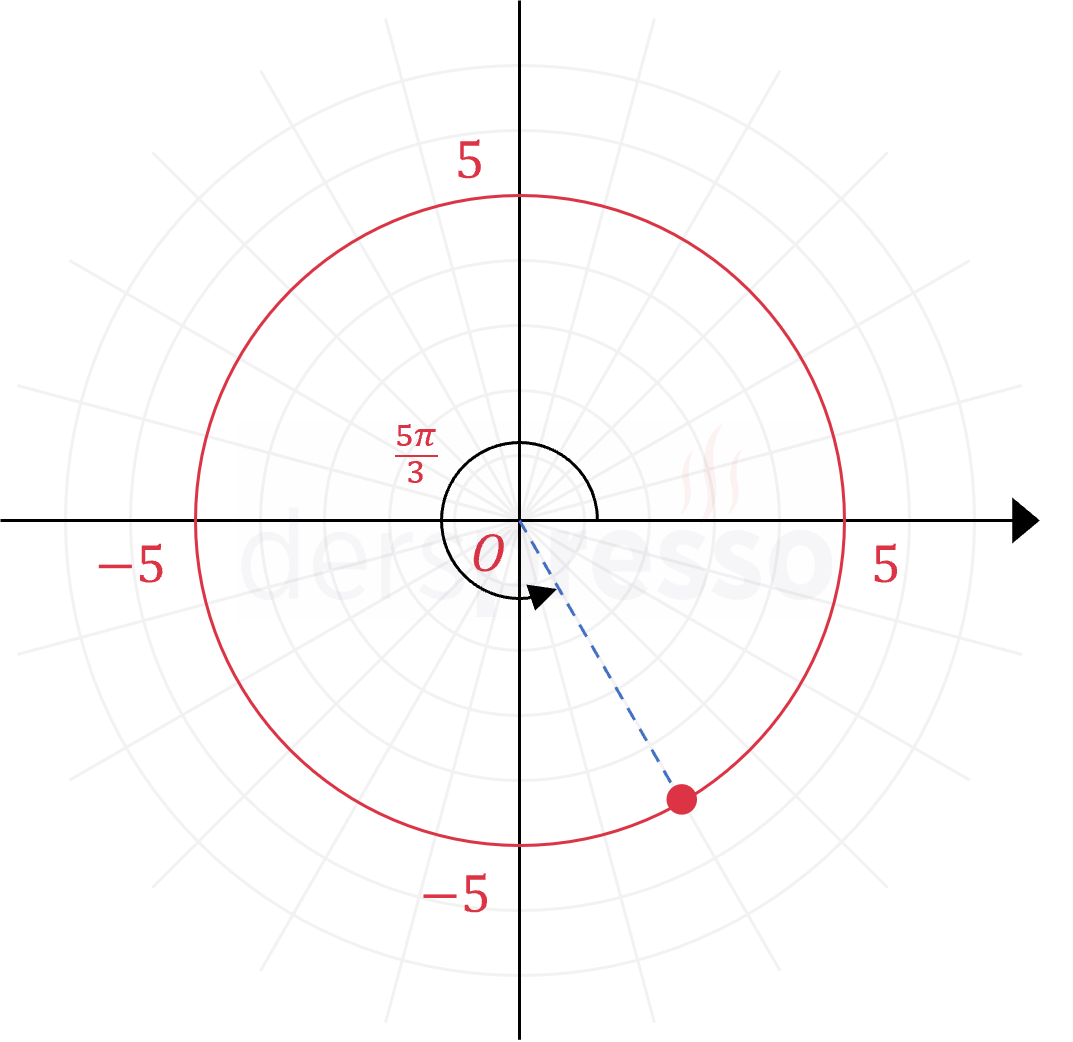
Merkezi orijin olan çember Kartezyen denklemi: \( x^2 + y^2 = 5^2 \) Kutupsal denklem: Çemberin kutupsal denkleminde \( (r_0, \beta) = (0, 0) \) yazıldığında aşağıdaki iki denklem elde edilir. \( r = 5 \) veya \( r = -5 \) Örnek nokta: \( (r, \theta) = (5, \frac{5\pi}{3}) \) |

|
Merkezi \( (R, 0) \) olan çember Kartezyen denklemi: \( (x - 3)^2 + y^2 = 3^2 \) Kutupsal denklem: Çemberin kutupsal denkleminde \( (r_0, \beta) = (3, 0) \) yazıldığında aşağıdaki denklem elde edilir. \( r = 6\cos{\theta} \) Örnek denklem sadece kosinüs fonksiyonu içerdiği için kutup eksenine göre simetriktir. Örnek nokta: \( r = 6\cos{\frac{\pi}{3}} = 3 \) \( (r, \theta) = (3, \frac{\pi}{3}) \) |

|
Merkezi \( (0, R) \) olan çember Kartezyen denklemi: \( x^2 + (y + 2)^2 = 2^2 \) Kutupsal denklem: Çemberin kutupsal denkleminde \( (r_0, \beta) = (-2, \frac{\pi}{2}) \) yazıldığında aşağıdaki denklem elde edilir. \( r = -4\sin{\theta} \) Örnek denklem sadece sinüs fonksiyonu içerdiği için \( \theta = \frac{\pi}{2} \) doğrusuna göre simetriktir. Örnek nokta: \( r = -4\sin{\frac{3\pi}{2}} = 4 \) \( (r, \theta) = (4, \frac{3\pi}{2}) \) |
|
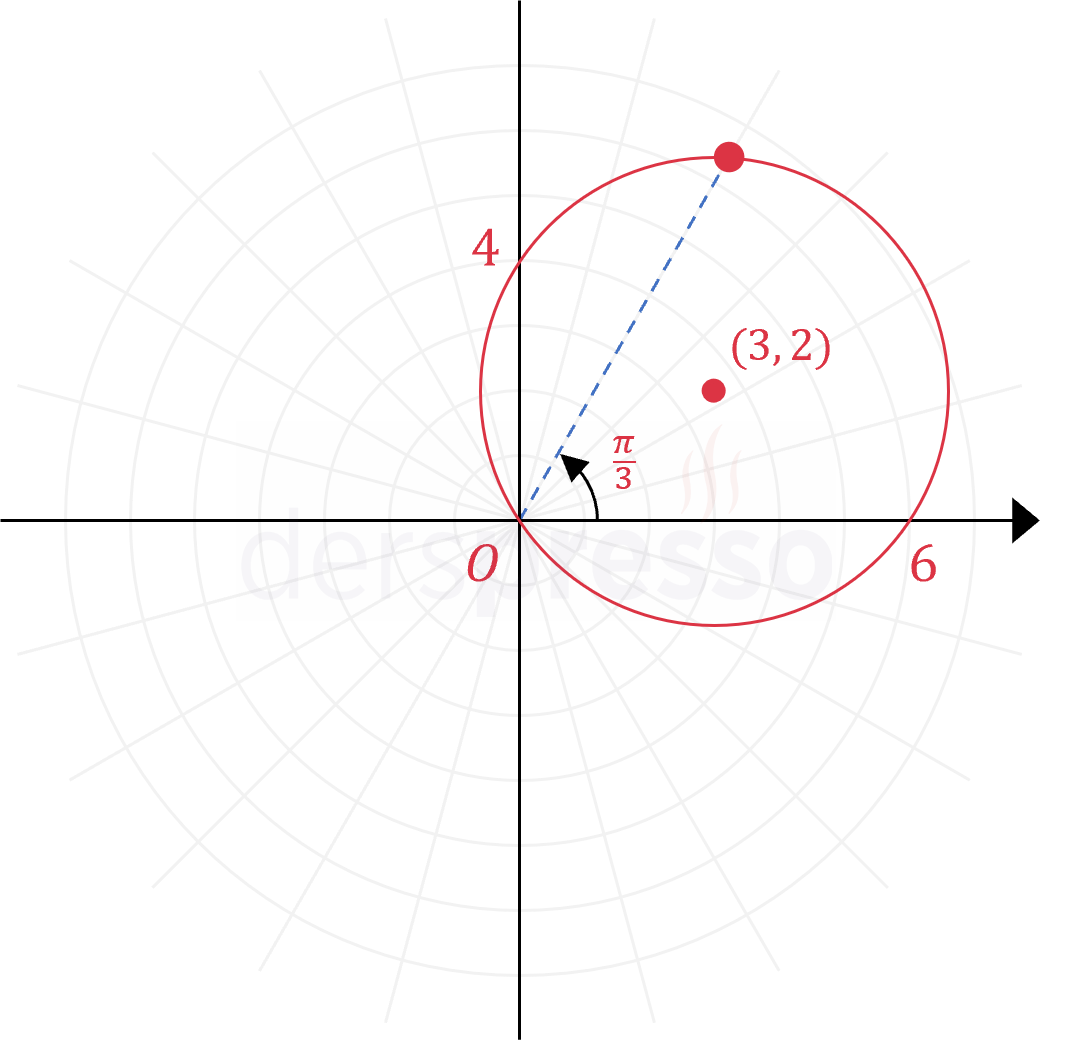
Orijinden geçen çember Kartezyen denklemi: \( (x - 3)^2 + (y - 2)^2 = 3^2 + 2^2 \) Kutupsal denklem: \( r = 6\cos{\theta} + 4\sin{\theta} \) Örnek nokta: \( r = 6\cos{\frac{\pi}{3}} + 4\sin{\frac{\pi}{3}} = 3 + 2\sqrt{3} \) \( (r, \theta) = (3 + 2\sqrt{3}, \frac{\pi}{3}) \) |
Limaçon Eğrisi
Fransızcada salyangoz anlamına gelen limaçon eğrilerinin genel denklemi aşağıdaki gibidir.
Limaçon eğrisi kutupsal denklemi:
\( a, b \in \mathbb{R} \)
\( a \gt 0, b \gt 0 \) olmak üzere,
\( r = a \pm b\sin{\theta} \)
\( r = a \pm b\cos{\theta} \)
Limaçon eğrilerinin şekli \( a \) ve \( b \) değerlerinin birbirine oranına göre aşağıda grafikleri verilen dört şekilde olabilir. Her bir limaçon tipinde \( b \)'nin önündeki işarete ve trigonometrik fonksiyona göre şekil aşağıdaki şekilde değişir.
- Sinüs fonksiyonu ve \( b \)'nin önündeki işaret pozitif: Şeklin çukur kısmı aşağı bakar.
- Sinüs fonksiyonu ve \( b \)'nin önündeki işaret negatif: Şeklin çukur kısmı yukarı bakar.
- Kosinüs fonksiyonu ve \( b \)'nin önündeki işaret pozitif: Şeklin çukur kısmı sola bakar.
- Kosinüs fonksiyonu ve \( b \)'nin önündeki işaret negatif: Şeklin çukur kısmı sağa bakar.
Sinüs fonksiyonu içeren limaçon eğrileri önceki bölümde gördüğümüz simetri prensiplerine göre \( \theta = \frac{\pi}{2} \) doğrusuna göre simetriktir. Kosinüs fonksiyonu içeren limaçon eğrileri ise kutup eksenine göre simetriktir.
Aşağıda farklı limaçon eğrilerinin kutupsal denklemleri ve grafikleri verilmiştir.
| Grafik | Denklem |
|---|---|
|
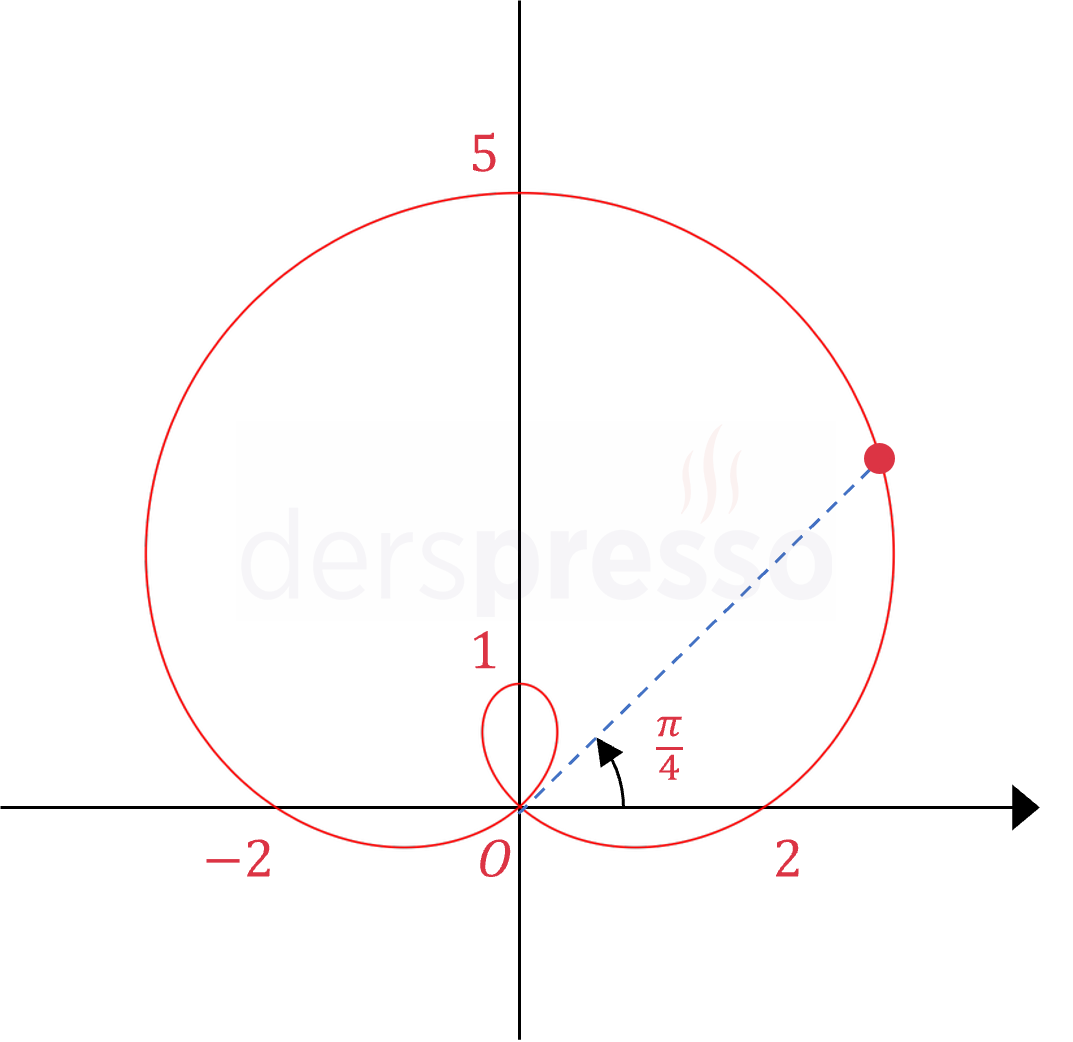
İç döngülü limaçon \( \dfrac{a}{b} \lt 1 \) Bu eğriler içe doğru bir döngü yapar. \( r = 2 + 3\sin{\theta} \) Örnek denklem sadece sinüs fonksiyonu içerdiği için \( \theta = \frac{\pi}{2} \) doğrusuna göre simetriktir. Örnek nokta: \( r = 2 + 3\sin{\frac{\pi}{4}} = 2 + \frac{3\sqrt{2}}{2} \) \( (r, \theta) = (2 + \frac{3\sqrt{2}}{2}, \frac{\pi}{4}) \) |
|
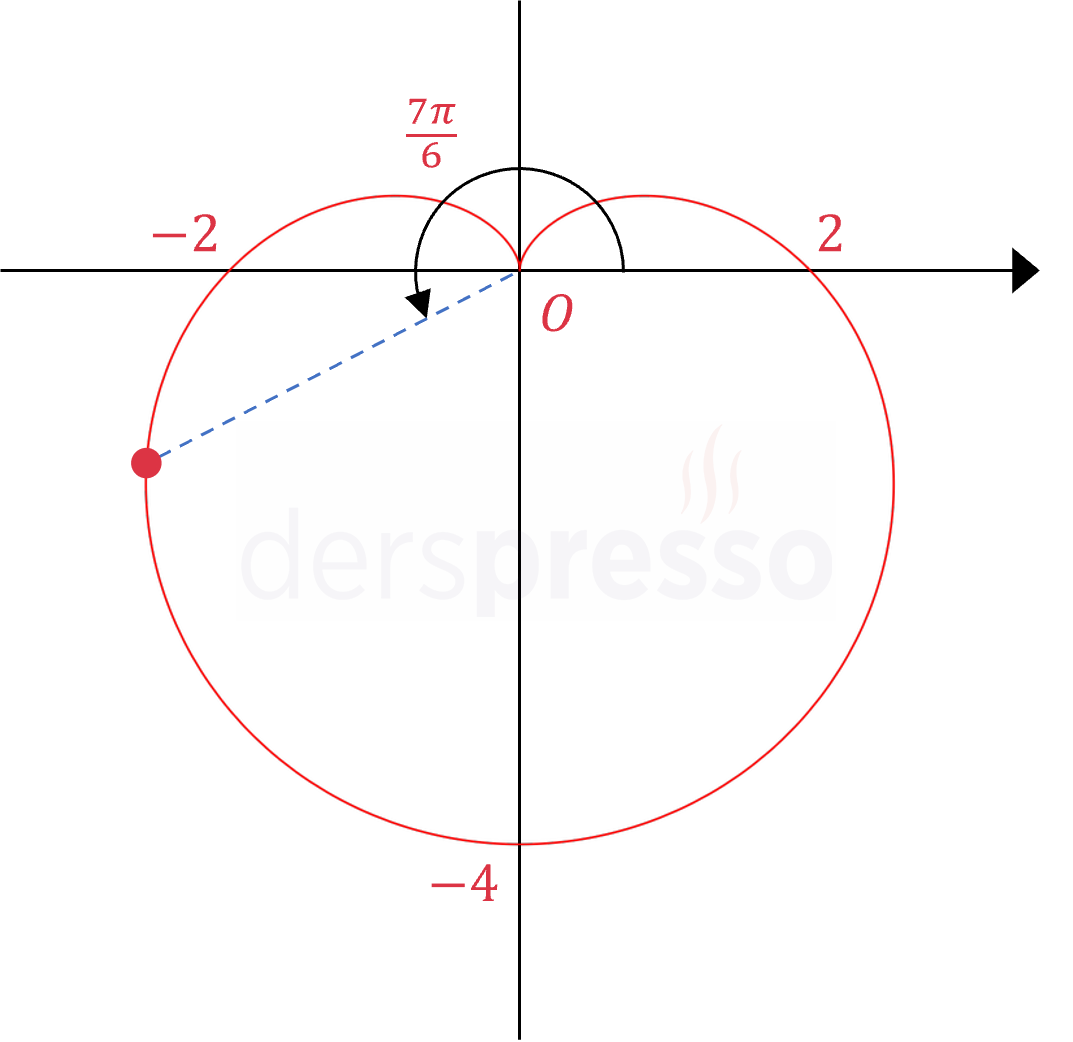
Kardiyoit \( \dfrac{a}{b} = 1 \) Bu eğriler kalp şeklindedir ve iç döngülü ve çukurlu limaçon arasındaki formdur. \( r = 2 - 2\sin{\theta} \) Örnek denklem sadece sinüs fonksiyonu içerdiği için \( \theta = \frac{\pi}{2} \) doğrusuna göre simetriktir. Örnek nokta: \( r = 2 - 2\sin{\frac{7\pi}{6}} = 3 \) \( (r, \theta) = (3, \frac{7\pi}{6}) \) |

|
Çukurlu limaçon \( 1 \lt \dfrac{a}{b} \lt 2 \) Bu eğriler konkavdır. \( r = 3 + 2\cos{\theta} \) Örnek denklem sadece kosinüs fonksiyonu içerdiği için kutup eksenine göre simetriktir. Örnek nokta: \( r = 3 + 2\sin{\frac{7\pi}{4}} = 3 - \sqrt{2} \) \( (r, \theta) = (3 - \sqrt{2}, \frac{7\pi}{4}) \) |
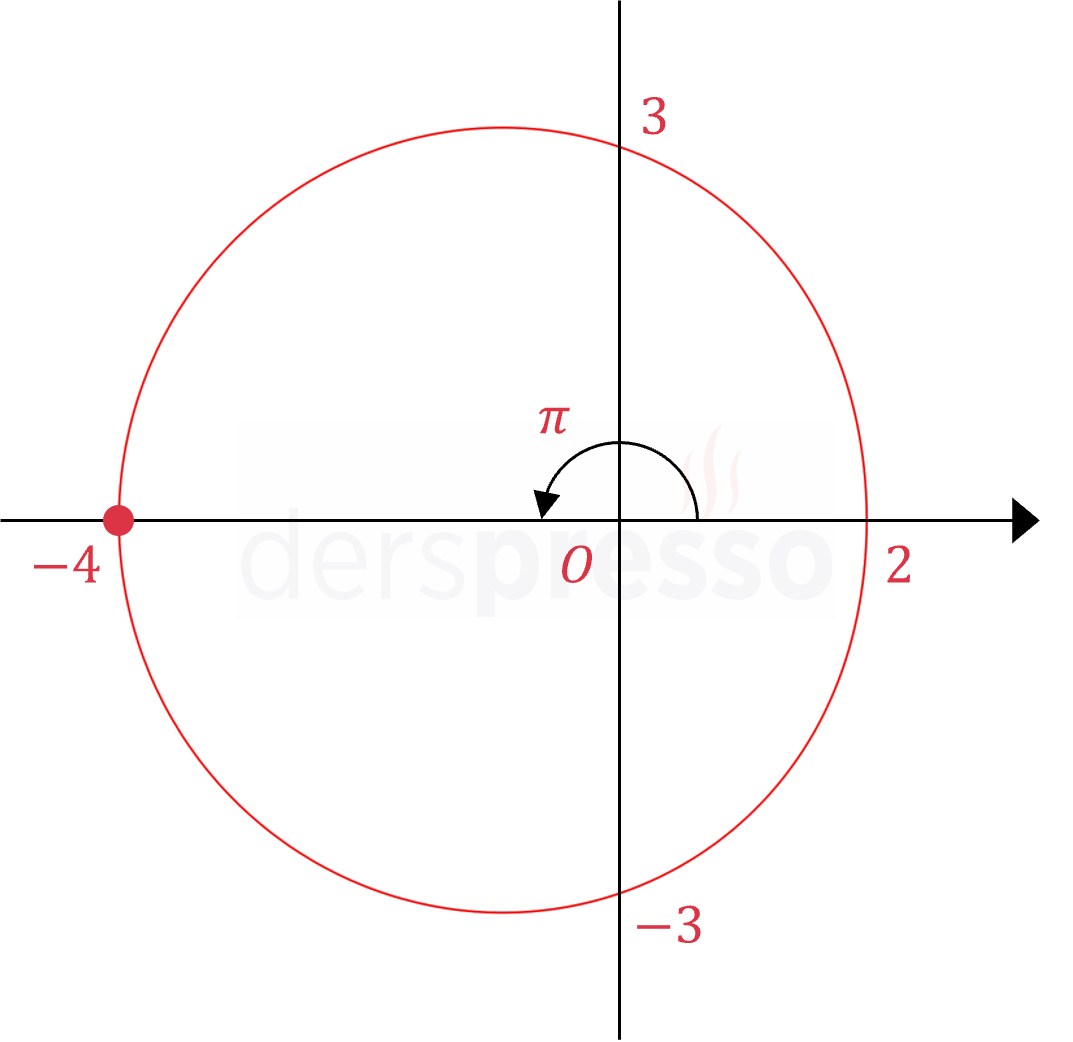
|
Konveks limaçon \( \dfrac{a}{b} \gt 2 \) Bu eğriler konveksdir. \( r = 3 - \cos{\theta} \) Örnek denklem sadece kosinüs fonksiyonu içerdiği için kutup eksenine göre simetriktir. Örnek nokta: \( r = 3 - \cos{\pi} = 4 \) \( (r, \theta) = (4, \pi) \) |
Gül Eğrisi
Grafikleri bir çiçeğin yapraklarını andıran gül eğrilerinin genel denklemi aşağıdaki gibidir.
Gül eğrisi kutupsal denklemi:
\( a \in \mathbb{R}, k \in \mathbb{Z^+} \)
\( a \ne 0, k \gt 1 \) olmak üzere,
\( r = a\sin(k\theta) \)
\( r = a\cos(k\theta) \)
Gül eğrilerinde \( k \) tek sayı ise eğri \( k \) kadar yapraktan, çift sayı ise \( 2k \) kadar yapraktan oluşur. \( k \) katsayısı yaprak sayısını belirlerken \( a \) katsayısı yaprakların yüksekliğini belirler.
Gül eğrilerinde \( k \) tek sayı ise eğrinin periyodu \( \pi \), çift sayı ise \( 2\pi \) olur.
Aşağıda farklı gül eğrilerinin kutupsal denklemleri ve grafikleri verilmiştir.
| Grafik | Denklem |
|---|---|
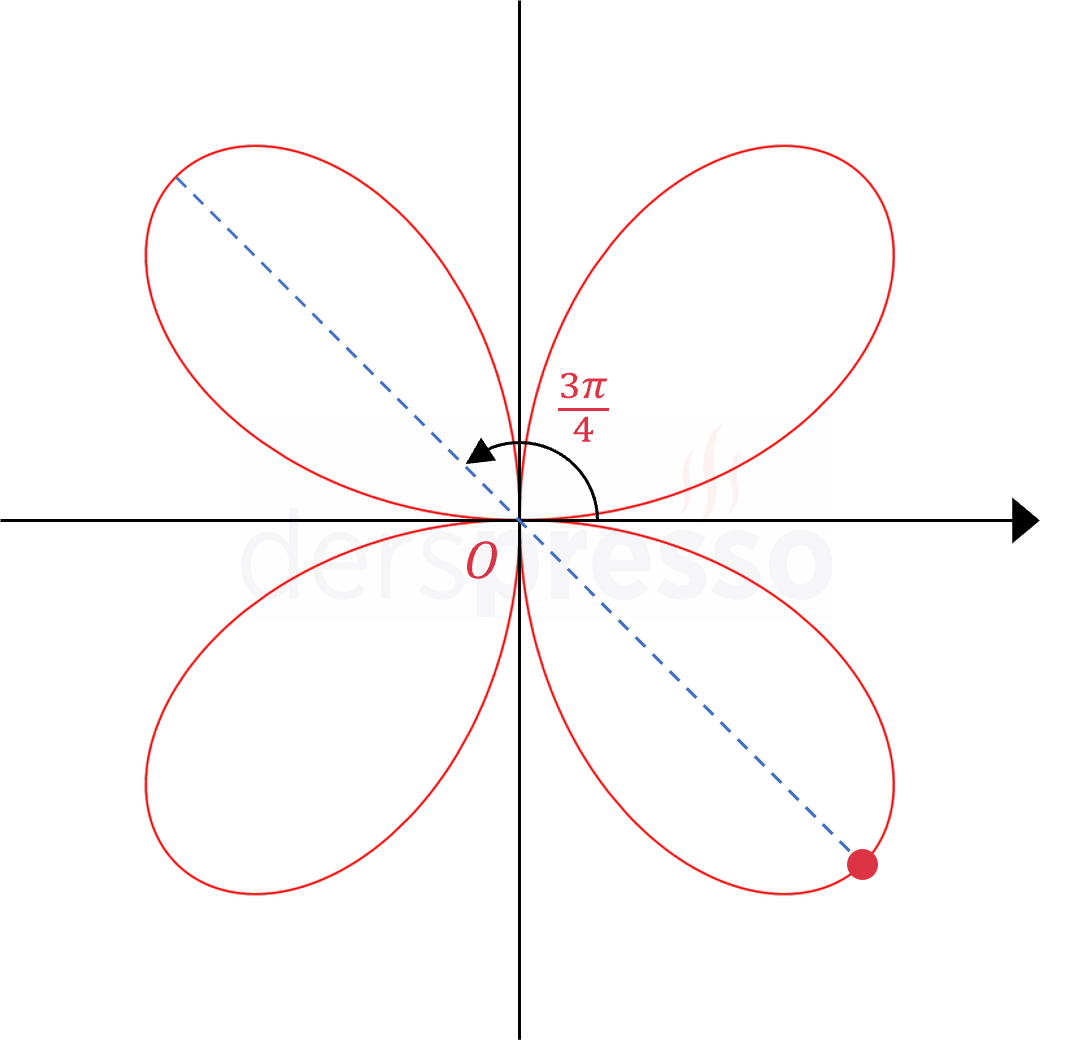
|
\( k = 2 \) \( r = 3\sin(2\theta) \) \( k \) çift sayı olduğu için eğri \( 2k = 4 \) yapraklıdır ve periyodu \( 2\pi \)'dir. Örnek denklem sadece sinüs fonksiyonu içerdiği için \( \theta = \frac{\pi}{2} \) doğrusuna göre simetriktir. Denklem ayrıca kutup ekseni ve kutup noktasına göre simetri koşullarını sağladığı için bu iki simetriye de sahiptir. Örnek nokta: \( r = 3\sin(2\frac{3\pi}{4}) = -3 \) \( (r, \theta) = (-3, \frac{3\pi}{4}) \) |

|
\( k = 3 \) \( r = 3\sin(3\theta) \) \( k \) tek sayı olduğu için eğri \( k = 3 \) yapraklıdır ve periyodu \( \pi \)'dir. Örnek denklem sadece sinüs fonksiyonu içerdiği için \( \theta = \frac{\pi}{2} \) doğrusuna göre simetriktir. Örnek nokta: \( r = 3\sin(3\frac{\pi}{3}) = 0 \) \( (r, \theta) = (0, \frac{\pi}{3}) \) |
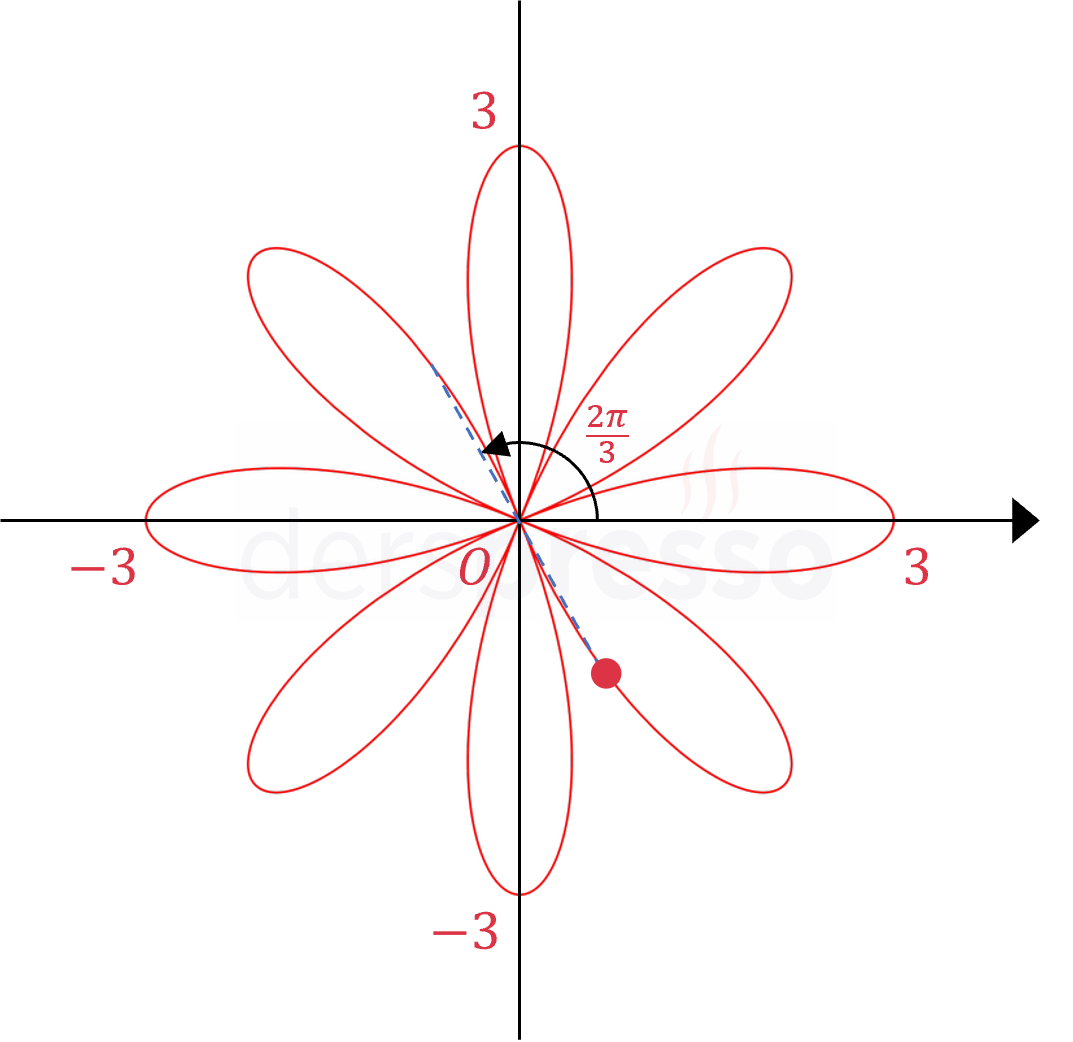
|
\( k = 4 \) \( r = 3\cos(4\theta) \) \( k \) çift sayı olduğu için eğri \( 2k = 8 \) yapraklıdır ve periyodu \( 2\pi \)'dir. Örnek denklem sadece kosinüs fonksiyonu içerdiği için kutup eksenine göre simetriktir. Denklem ayrıca \( \theta = \frac{\pi}{2} \) doğrusuna ve kutup noktasına göre simetri koşullarını sağladığı için bu iki simetriye de sahiptir. Örnek nokta: \( r = 3\cos(4\frac{2\pi}{3}) = -\frac{3}{2} \) \( (r, \theta) = (-\frac{3}{2}, \frac{2\pi}{3}) \) |

|
\( k = 5 \) Örnek eğri: \( r = 3\cos(5\theta) \) \( k \) tek sayı olduğu için eğri \( k = 5 \) yapraklıdır ve periyodu \( \pi \)'dir. Örnek denklem sadece kosinüs fonksiyonu içerdiği için kutup eksenine göre simetriktir. Örnek nokta: \( r = 3\cos(5\frac{2\pi}{5}) = 3 \) \( (r, \theta) = (3, \frac{2\pi}{5}) \) |
Arşimet Spirali
Arşimet spirallerinin genel denklemi aşağıdaki gibidir.
Spiralin kutupsal denklemi:
\( r = a + b\theta \)
Bu eğride \( a \) kaysayısı spiralin kutup ekseni üzerindeki ilk konumunu, \( b \) kaysayısı da spiralin ardışık dönüşleri arasındaki mesafeyi belirler.
Bu eğriler her dönüşte farklı \( r \) değerleri aldıkları için herhangi bir simetri içermezler.
Aşağıda farklı Arşimet spirallerinin kutupsal denklemleri ve grafikleri verilmiştir.
| Grafik | Denklem |
|---|---|
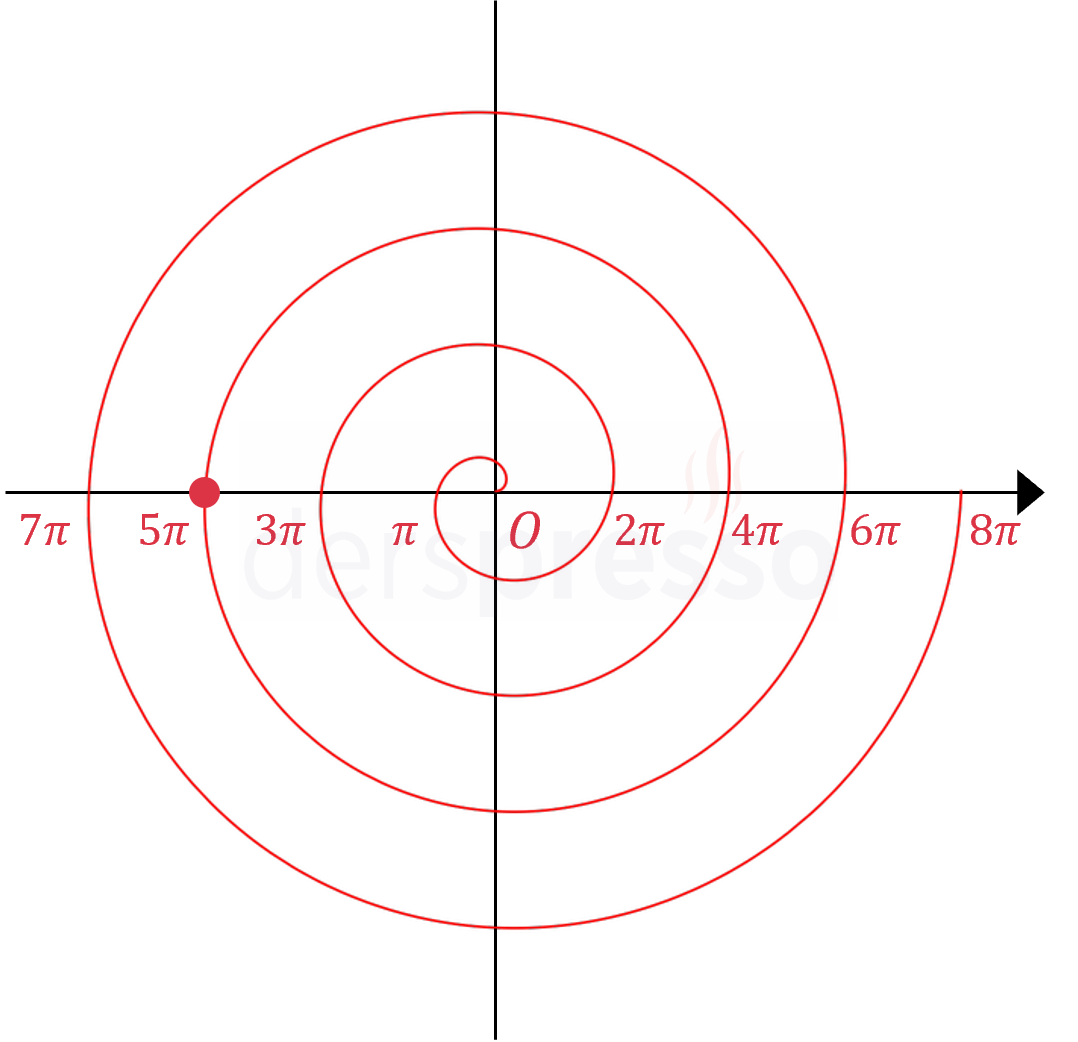
|
\( r = \theta \) \( a = 0 \) olduğu için spiralin başlangıç noktası orijindir. Örnek nokta: \( r = 5\pi \) \( (r, \theta) = (5\pi, 5\pi) \) |
|
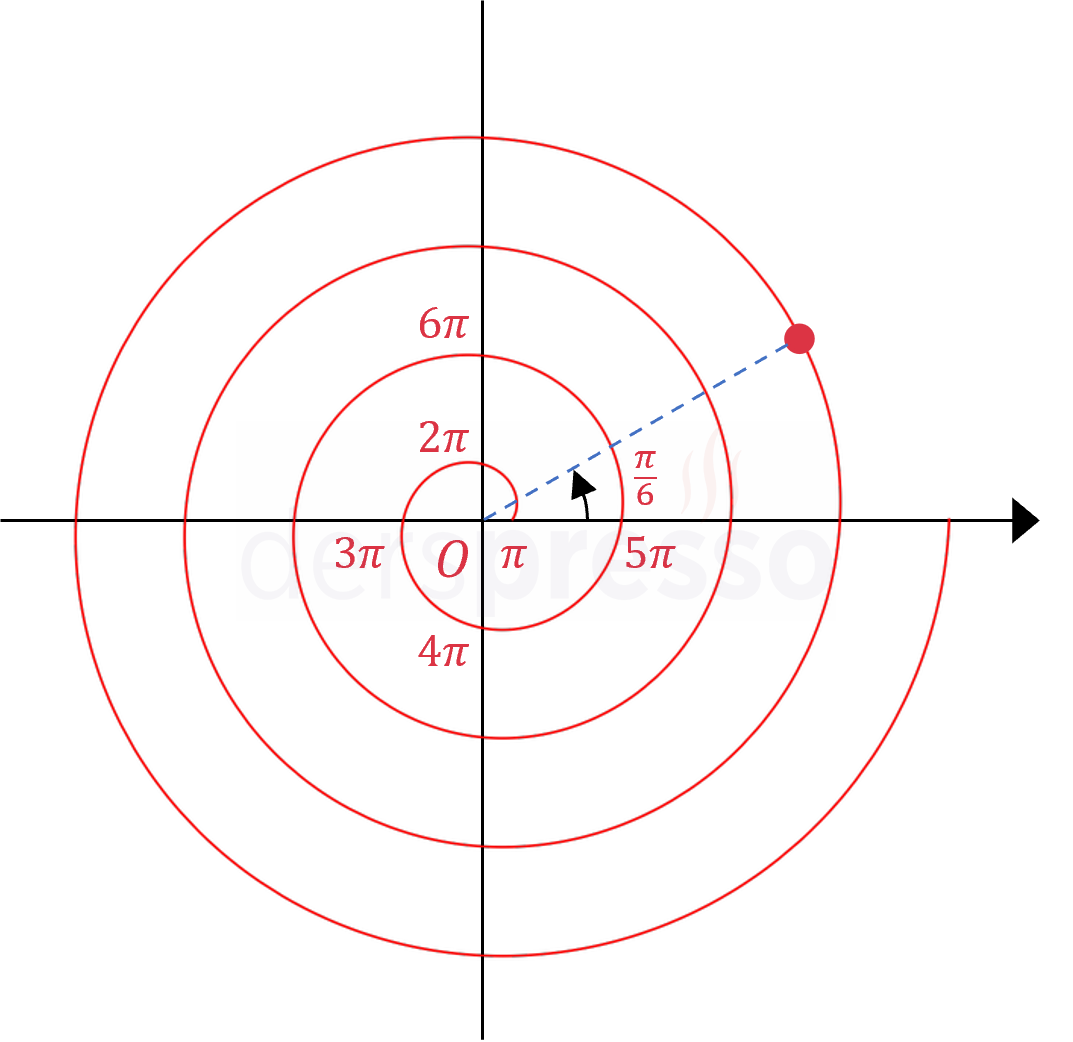
\( r = \pi + 2\theta \) \( a = \pi \) olduğu için spiralin başlangıç noktası \( \pi \) kadar sağa ötelenir. Örnek nokta: \( r = \pi + 2\frac{\pi}{6} \) \( (r, \theta) = (\frac{4\pi}{3}, \frac{\pi}{6}) \) |
Konikler
Koniklerin genel denklemi aşağıdaki gibidir.
Konik kutupsal denklemi:
\( d \): Odağın doğrultmana uzaklığı
\( e \): Koniğin dış merkezliği (konik üzerindeki bir noktanın odağa ve doğrultmana uzaklıklarının oranı)
\( r = \dfrac{ed}{1 \pm e\cos{\theta}} \)
\( r = \dfrac{ed}{1 \pm e\sin{\theta}} \)
Aşağıda farklı koniklerin kutupsal denklemleri ve grafikleri verilmiştir.
| Grafik | Denklem |
|---|---|

|
Çember \( e = 0 \) \( r = 4 \) Örnek nokta: \( (r, \theta) = (4, \frac{13\pi}{19}) \) |

|
Elips \( 0 \lt e \lt 1 \) \( r = \dfrac{2}{1 + \frac{3}{4}\cos{\theta}} \) Örnek nokta: \( r = \dfrac{2}{1 + \frac{3}{4}\cos{\pi}} = 8 \) \( (r, \theta) = (8, \pi) \) |

|
Parabol \( e = 1 \) \( r = \dfrac{2}{1 + \cos{\theta}} \) Örnek nokta: \( r = \dfrac{2}{1 + \cos{\frac{2\pi}{3}}} = 4 \) \( (r, \theta) = (4, \frac{2\pi}{3}) \) |
|
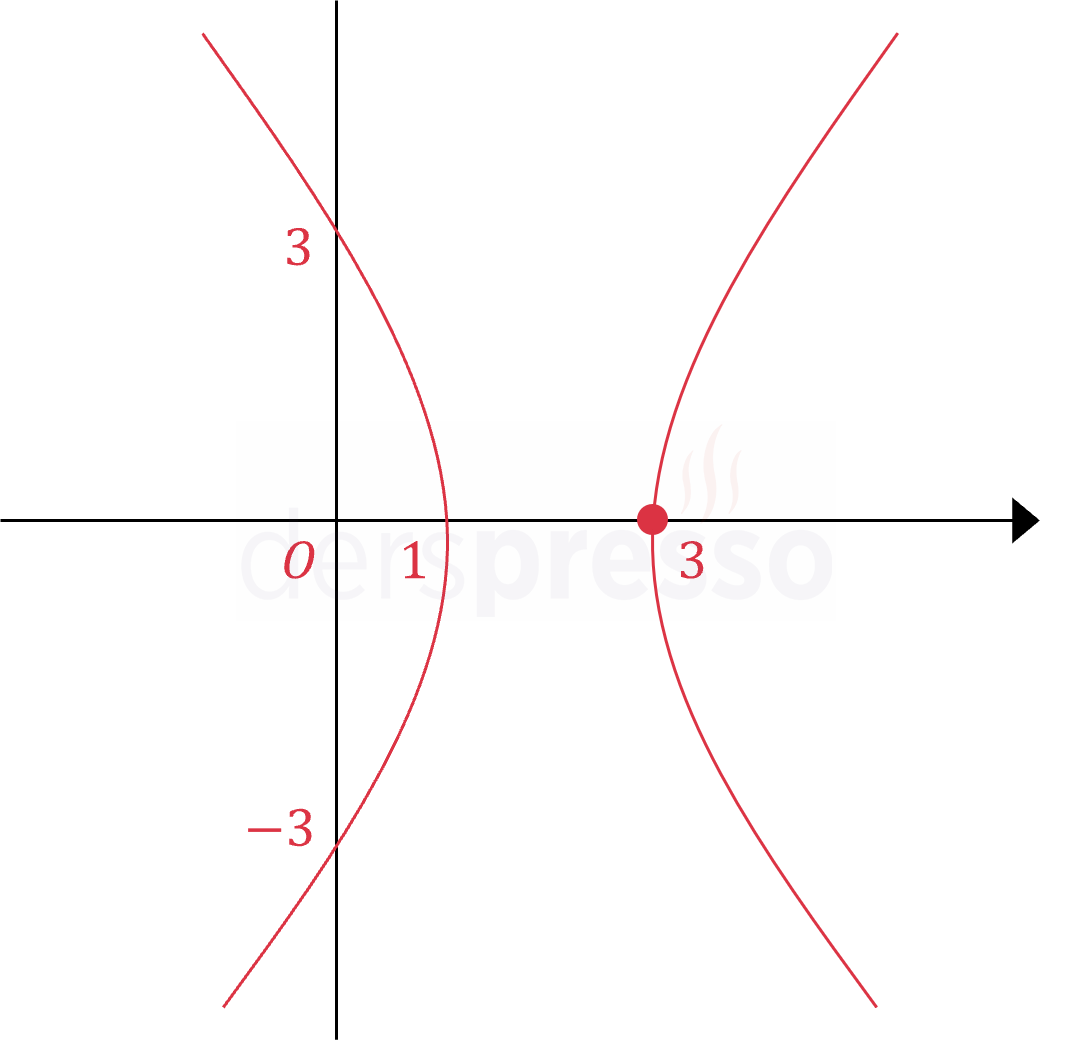
Hiperbol \( e \gt 1 \) \( r = \dfrac{3}{1 + 2\cos{\theta}} \) Örnek nokta: \( r = \dfrac{3}{1 + 2\cos{\pi}} = -3 \) \( (r, \theta) = (-3, \pi) \) |