Koordinat Düzleminde Çember
Koordinat düzleminde bir noktaya eşit uzaklıktaki noktaların kümesi bir çember oluşturur. Bu noktaya çemberin merkezi, çemberin üzerindeki noktaların merkeze uzaklığına çemberin yarıçapı denir.

\( r \in \mathbb{R^+} \) olmak üzere,
\( M(a, b) \): Çemberin merkezi
\( r \): Çemberin yarıçapı
\( \abs{AM} = \abs{BM} = \abs{CM} = r \)
Çemberin Standart Denklemi
Merkezi \( M(a, b) \) ve yarıçapı \( r \) olan bir çemberin standart denklemi aşağıdaki gibidir:
\( (x - a)^2 + (y - b)^2 = r^2 \)
\( M(5, -2) \) merkezli ve \( 3 \) birim yarıçaplı çemberin standart denklemi:
\( (x - 5)^2 + (y - (-2))^2 = 3^2 \)
\( (x - 5)^2 + (y + 2)^2 = 9 \)
İSPATI GÖSTER
Çemberin merkezi olan \( M(a, b) \) noktasına eşit ve \( r \) birim uzaklıktaki tüm noktaları \( A(x, y) \) ile ifade edersek, \( A \) noktasının geometrik yer denklemini iki nokta arasındaki uzaklık formülünden aşağıdaki şekilde yazabiliriz:
\( \abs{AM} = r \)
\( \sqrt{(x - a)^2 + (y - b)^2} = r \)
İki tarafın karesini alalım:
\( (x - a)^2 + (y - b)^2 = r^2 \)
Merkezi orijinde olan çembere merkezil çember denir. Merkezil çemberin denklemi aşağıdaki gibidir:
\( x^2 + y^2 = r^2 \)
Bir çemberin denklemini yazabilmemiz için aşağıdakilerden birine ihtiyacımız vardır:
- Çemberin merkezi ve yarıçapı
- Çemberin geçtiği üç farklı nokta
Çemberin Genel Denklemi
Çemberin standart denkleminin aşağıdaki biçimde açık yazılışına çemberin genel denklemi denir:
\( x^2 + y^2 + Dx + Ey + F = 0 \)
\( D = -2a \)
\( E = -2b \)
\( F = a^2 + b^2 - r^2 \)
Bu denklemde çemberin merkezi ve yarıçapı aşağıdaki gibi olmaktadır:
\( M(a, b) = M(-\frac{D}{2}, -\frac{E}{2}) \)
\( r = \frac{1}{2} \sqrt{D^2 + E^2 - 4F} \)
\( x^2 + y^2 - 10x + 4y + 20 = 0 \)
Genel denklemi yukarıdaki gibi olan çemberin merkezi ve yarıçapı:
\( M(-\frac{D}{2}, -\frac{E}{2}) = M(5, -2) \)
\( r = \frac{1}{2} \sqrt{(-10)^2 + 4^2 - 4 \cdot 20} = 3 \)
İSPATI GÖSTER
Çemberin standart denklemini açık haliyle yazalım:
\( (x - a)^2 + (y - b)^2 = r^2 \)
\( x^2 - 2ax + a^2 + y^2 - 2by + b^2 - r^2 = 0 \)
\( x^2 + y^2 - 2ax - 2by + a^2 + b^2 - r^2 = 0 \)
Bu denkleme aşağıdaki değişken değiştirmeleri uygulayalım:
\( D = -2a \)
\( E = -2b \)
\( F = a^2 + b^2 - r^2 \)
Bu durumda denklem aşağıdaki genel denklem formatına dönüşecektir:
\( x^2 + y^2 + Dx + Ey + F = 0 \)
Konum ve Katsayı İlişkileri
Bir çemberin eksenlere ve orijine göre konumu ile \( D \), \( E \) ve \( F \) değerleri arasında aşağıdaki ilişkileri kurabiliriz.
\( \left( \dfrac{D}{2} \right)^2 = F \) ise çember \( x \) eksenine teğettir.
\( x^2 + y^2 - 10x + 4y + 25 = 0 \)
\( (\frac{-10}{2})^2 = 25 \) olduğu için çember \( x \) eksenine teğettir.
\( (x - 5)^2 + (y + 2)^2 = 2^2 \)
İSPATI GÖSTER
\( \left( \dfrac{D}{2} \right)^2 = F \) ise,
\( D \) ve \( F \) katsayılarının açık hallerini yerine koyalım.
\( D = -2a \)
\( F = a^2 + b^2 - r^2 \)
\( \left( \dfrac{-2a}{2} \right)^2 = a^2 + b^2 - r^2 \)
\( \dfrac{4a^2}{4} = a^2 + b^2 - r^2 \)
\( a^2 = a^2 + b^2 - r^2 \)
\( b^2 = r^2 \)
\( r \gt 0 \) olduğu için,
\( b = \pm r \)
Bu durumda denklem aşağıdaki formatta olur, dolayısıyla çember \( x \) eksenine teğettir.
\( (x - a)^2 + (y \pm r)^2 = r^2 \)
\( \left( \dfrac{E}{2} \right)^2 = F \) ise çember \( y \) eksenine teğettir.
\( x^2 + y^2 + 6x + 12y + 36 = 0 \)
\( (\frac{12}{2})^2 = 36 \) olduğu için çember \( y \) eksenine teğettir.
\( (x + 3)^2 + (y + 6)^2 = 3^2 \)
İSPATI GÖSTER
\( \left( \dfrac{E}{2} \right)^2 = F \) ise,
\( E \) ve \( F \) katsayılarının açık hallerini yerine koyalım.
\( E = -2b \)
\( F = a^2 + b^2 - r^2 \)
\( \left( \dfrac{-2b}{2} \right)^2 = a^2 + b^2 - r^2 \)
\( \dfrac{4b^2}{4} = a^2 + b^2 - r^2 \)
\( b^2 = a^2 + b^2 - r^2 \)
\( a^2 = r^2 \)
\( r \gt 0 \) olduğu için,
\( a = \pm r \)
Bu durumda denklem aşağıdaki formatta olur, dolayısıyla çember \( y \) eksenine teğettir.
\( (x \pm r)^2 + (y - b)^2 = r^2 \)
\( \left( \dfrac{D}{2} \right)^2 = {\left( \dfrac{E}{2} \right)}^2 = F \) ise çember \( x \) ve \( y \) eksenlerine teğettir.
\( x^2 + y^2 + 6x - 6y + 9 = 0 \)
\( (\frac{6}{2})^2 = (\frac{-6}{2})^2 = 36 \) olduğu için çember \( x \) ve \( y \) eksenlerine teğettir.
\( (x + 3)^2 + (y - 3)^2 = 3^2 \)
İSPATI GÖSTER
\( \left( \dfrac{D}{2} \right)^2 = \left( \dfrac{E}{2} \right)^2 = F \) ise,
\( D \), \( E \) ve \( F \) katsayılarının açık hallerini yerine koyalım.
\( D = -2a \)
\( E = -2b \)
\( F = a^2 + b^2 - r^2 \)
\( \left( \dfrac{-2a}{2} \right)^2 = a^2 + b^2 - r^2 \)
\( b = \pm r \)
\( \left( \dfrac{-2b}{2} \right)^2 = a^2 + b^2 - r^2 \)
\( a = \pm r \)
Buna göre aşağıdaki eşitliği elde ederiz.
\( a = b = \pm r \)
Bu durumda denklem aşağıdaki formatta olur, dolayısıyla çember \( x \) ve \( y \) eksenlerine teğettir.
\( (x \pm r)^2 + (y \pm r)^2 = r^2 \)
\( F = 0 \) ise çember orijinden geçer.
\( x^2 + y^2 - 6x - 8y = 0 \)
\( F = 0 \) olduğu için çember orijinden geçer.
\( (x - 3)^2 + (y - 4)^2 = 5^2 \)
İSPATI GÖSTER
\( F = 0 \) ise,
Denklem aşağıdaki formatta olur.
\( x^2 + y^2 + Dx + Ey = 0 \)
Denklemde sabit terim bulunmadığı için O(0, 0) noktası denklemi sağlar.
\( 0^2 + 0^2 + D(0) + E(0) = 0 \)
\( 0 = 0 \)
Dolayısıyla çemberin orijinden geçtiğini söyleyebiliriz.
Bir Denklemin Çember Olma Koşulları
Verilen bir denklemin bir çember belirtmesi için aşağıdaki koşulların sağlanması gerekir:
- Denklem sadece \( x^2 \), \( y^2 \), \( x \) ve \( y \)'li terimler ve sabit terim içerebilir. Denklemde \( x \) ve \( y \)'nin diğer kuvvetleri ya da \( xy \) gibi terimler bulunmamalıdır.
- \( x^2 \) ve \( y^2 \) terimlerinin katsayıları birbirine eşit ve \( 1 \) olmalıdır. Eğer katsayıları \( 1 \)'den farklı ise tüm terimler bu katsayıya bölünmeli ve her iki terimin katsayısı \( 1 \)'e getirilmelidir.
- Çemberin yarıçapı sıfırdan büyük, yani \( r = \frac{1}{2} \sqrt{D^2 + E^2 - 4F} \gt 0 \) olmalıdır.
İlk iki koşulu sağlayan, ama yarıçap değeri sıfır olan bir denklem koordinat düzleminde bir nokta belirtir.
Merkezi ve yarıçapı verilen aşağıdaki çemberlerin standart denklemini yazınız.
(a) \( M(3, 2), \quad r = 5 \)
(b) \( M(3, -5), \quad r = \sqrt{11} \)
(c) \( M(-4, -1), \quad r = \sqrt{7} \)
(d) \( M(5\sqrt{2}, 0), \quad r = 3 \)
(e) \( M(0, 3), \quad r = \dfrac{2}{3} \)
Çözümü GösterMerkezi \( M(a, b) \) noktası ve yarıçapı \( r \) olan çemberin standart denklemi aşağıdaki gibidir.
\( (x - a)^2 + (y - b)^2 = r^2 \)
(a) seçeneği:
\( M(3, 2), \quad r = 5 \)
\( (x - 3)^2 + (y - 2)^2 = 5^2 \)
\( (x - 3)^2 + (y - 2)^2 = 25 \)
(b) seçeneği:
\( M(3, -5), \quad r = \sqrt{11} \)
\( (x - 3)^2 + (y - (-5))^2 = (\sqrt{11})^2 \)
\( (x - 3)^2 + (y + 5)^2 = 11 \)
(c) seçeneği:
\( M(-4, -1), \quad r = \sqrt{7} \)
\( (x - (-4))^2 + (y - (-1))^2 = (\sqrt{7})^2 \)
\( (x + 4)^2 + (y + 1)^2 = 7 \)
(d) seçeneği:
\( M(5\sqrt{2}, 0), \quad r = 3 \)
\( (x - 5\sqrt{2})^2 + (y - 0)^2 = 3^2 \)
\( (x - 5\sqrt{2})^2 + y^2 = 9 \)
(e) seçeneği:
\( M(0, 3), \quad r = \dfrac{2}{3} \)
\( (x - 0)^2 + (y - 3)^2 = (\dfrac{2}{3})^2 \)
\( x^2 + (y - 3)^2 = \dfrac{4}{9} \)
Standart denklemleri verilen aşağıdaki çemberlerin merkezini ve yarıçapını bulunuz.
(a) \( (x + 3)^2 + (y - 5)^2 = 16 \)
(b) \( (x - 1)^2 + y^2 = 17 \)
(c) \( (x + \sqrt{7})^2 + (y + 2)^2 = 2 \)
(d) \( (x + \dfrac{3}{4})^2 + (y - \dfrac{2}{5})^2 = \dfrac{1}{9} \)
Çözümü Göster\( (x - a)^2 + (y - b)^2 = r^2 \)
Standart denklemi yukarıdaki formda olan çemberin merkezi \( M(a, b) \) noktasıdır ve yarıçapı \( r \) birimdir.
(a) seçeneği:
\( (x + 3)^2 + (y - 5)^2 = 16 = 4^2 \)
Verilen çemberin merkezi \( M(-3, 5) \) noktasıdır ve yarıçapı 4 birimdir.
(b) seçeneği:
\( (x - 1)^2 + y^2 = 17 = (\sqrt{17})^2 \)
Verilen çemberin merkezi \( M(1, 0) \) noktasıdır ve yarıçapı \( \sqrt{17} \) birimdir.
(c) seçeneği:
\( (x + \sqrt{7})^2 + (y + 2)^2 = 2 = (\sqrt{2})^2 \)
Verilen çemberin merkezi \( M(-\sqrt{7}, -2) \) noktasıdır ve yarıçapı \( \sqrt{2} \) birimdir.
(d) seçeneği:
\( (x + \dfrac{3}{4})^2 + (y - \dfrac{2}{5})^2 = \dfrac{1}{9} = (\dfrac{1}{3})^2 \)
Verilen çemberin merkezi \( M(-\frac{3}{4}, \frac{2}{5}) \) noktasıdır ve yarıçapı \( \frac{1}{3} \) birimdir.
Genel denklemi \( x^2 + y^2 - 4x + 10y + 12 = 0 \) olan çemberin merkezinin koordinatlarını ve yarıçapını bulunuz.
Çözümü GösterYöntem 1:
Genel denklemi \( x^2 + y^2 + Dx + Ey + F = 0 \) şeklinde olan çemberin merkezi ve yarıçap uzunluğu aşağıdaki şekilde bulunur.
\( M(a, b) = M(-\dfrac{D}{2}, -\dfrac{E}{2}) \)
\( r = \dfrac{1}{2}\sqrt{D^2 + E^2 - 4F} \)
Verilen denklemdeki katsayıları bu formüllerde yerine koyalım.
\( M(-\dfrac{-4}{2}, -\dfrac{10}{2}) = M(2, -5) \)
\( r = \dfrac{1}{2}\sqrt{(-4)^2 + 10^2 - 4(12)} = \sqrt{17} \)
Yöntem 2:
Merkezi \( M(a, b) \) noktası ve yarıçapı \( r \) olan çemberin standart denklemi aşağıdaki gibidir.
\( (x - a) + (y - b)^2 = r^2 \)
Verilen denklemi düzenleyerek çemberin standart denklemi formuna getirelim.
\( x \) ve \( y \)'li terimleri tam kareye tamamlamak için denklemin sol tarafına 4 ve 25 ekleyip çıkaralım.
\( x^2 - 4x + 4 - 4 + y^2 + 10y + 25 - 25 + 12 = 0 \)
\( (x - 2)^2 + (y + 5)^2 - 17 = 0 \)
\( (x - 2) + (y + 5)^2 = (\sqrt{17})^2 \)
Buna göre çemberin merkezi \( M(2, -5) \) noktasıdır ve yarıçapı \( \sqrt{17} \) birimdir.
\( (3a - 8)x^2 + (5a - 16)y^2 + (2b + 6)xy + 4b = 0 \)
denklemi bir çember belirttiğine göre, çemberin yarıçapı kaçtır?
Çözümü GösterVerilen denklemin çember olabilmesi için aşağıdaki iki koşul sağlanmalıdır.
Koşul 1:
Denklem sadece \( x^2 \), \( y^2 \), \( x \) ve \( y \)'li terimler ve sabit terim içerebilir. Denklemde \( x \) ve \( y \)'nin diğer kuvvetleri ya da \( xy \) gibi terimler bulunmamalıdır.
Buna göre denklemde \( xy \)'li terimin katsayısı sıfır olmalıdır.
\( 2b + 6 = 0 \)
\( b = -3 \)
Koşul 2:
\( x^2 \) ve \( y^2 \)'li terimlerin katsayıları birbirine eşit ve 1 olmalıdır.
\( 3a - 8 = 5a - 16 \)
\( a = 4 \)
Bu değerleri kullanarak çemberin denklemini yazalım.
\( (3(4) - 8)x^2 + (5(4) - 16)y^2 + (2(-3) + 6)xy + 4(-3) = 0 \)
\( 4x^2 + 4y^2 - 12 = 0 \)
\( x^2 + y^2 = 3 = (\sqrt{3})^2 \)
Buna göre çemberin yarıçapı \( \sqrt{3} \) olarak bulunur.
Merkezi \( M(-3, 5) \) olan ve \( A(4, -2) \) noktasından geçen çemberin denklemini yazınız.
Çözümü GösterÇemberin merkezi ile üzerindeki herhangi bir nokta arasındaki mesafe çemberin yarıçapını verir.
Buna göre \( \abs{MA} \) uzaklığı çemberin yarıçapını verir.
İki nokta arasındaki uzaklık formülünü kullanalım.
\( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
\( \abs{MA} = r = \sqrt{(4 - (-3)^2 + (-2 - 5)^2} \)
\( = \sqrt{49 + 49} = 7\sqrt{2} \)
Merkezi \( M(a, b) \) noktası ve yarıçapı \( r \) olan çemberin standart denklemi aşağıdaki gibidir.
\( (x - a)^2 + (y - b)^2 = r^2 \)
\( (x - (-3))^2 + (y - 5)^2 = (7\sqrt{2})^2 \)
\( (x + 3)^2 + (y - 5)^2 = 98 \)
Orijine olan uzaklığı \( [2, 5) \) aralığında olan noktaları ifade eden eşitsizliği yazınız.
Çözümü GösterOrijine \( k \) birim uzaklıktaki noktaların kümesi, merkezi orijin ve yarıçapı \( k \) olan çemberdir.
\( (x, y) \) noktasının orijine olan uzaklığı \( \sqrt{x^2 + y^2} \) şeklinde ifade edilir.
Orijine olan uzaklığı \( [2, 5) \) aralığında olan noktaları aşağıdaki şekilde ifade edebiliriz.
\( 2 \le \sqrt{x^2 + y^2} \lt 5 \)
Eşitsizliğin taraflarının karesini alalım.
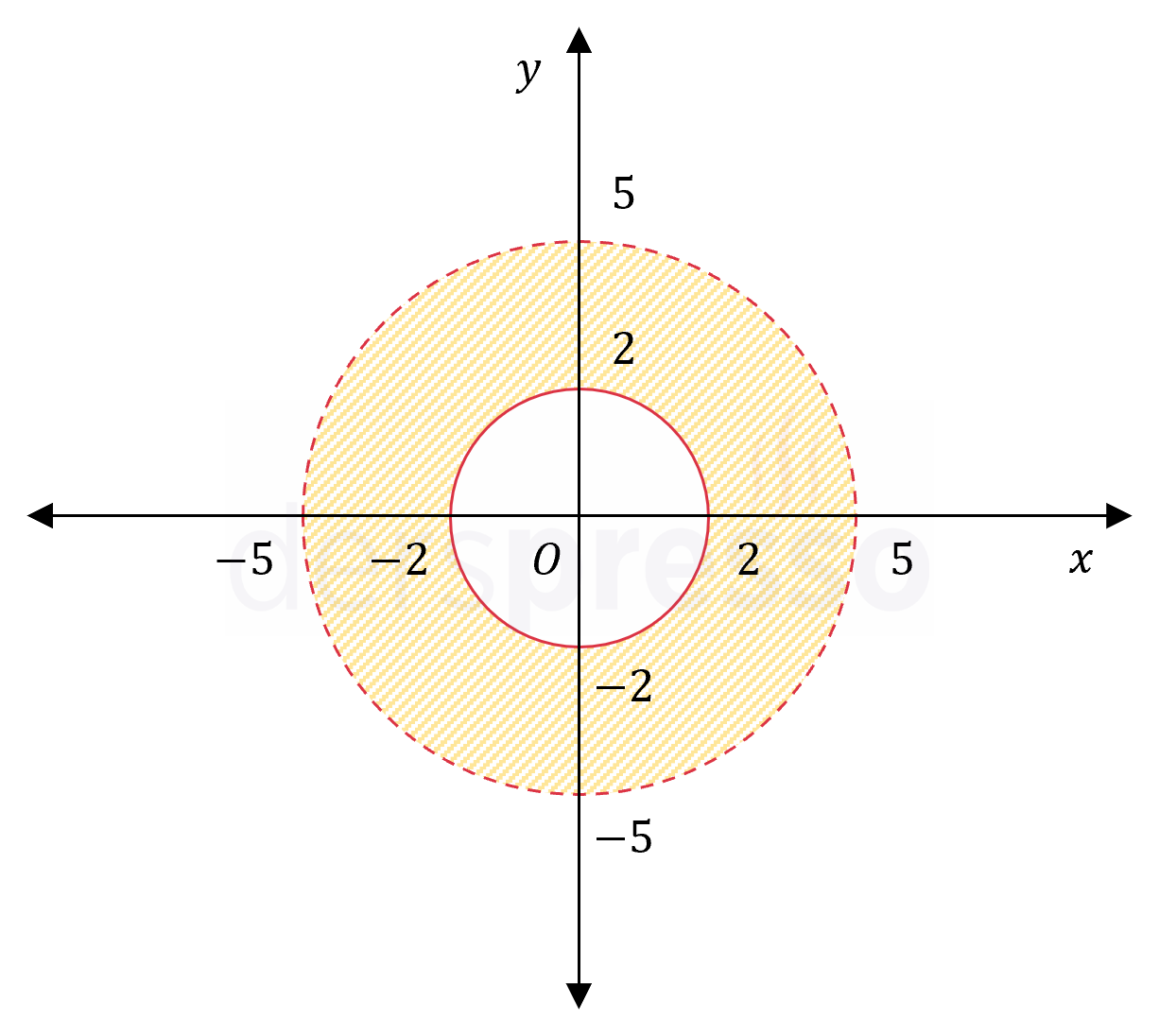
\( 4 \le x^2 + y^2 \lt 25 \) bulunur.
Bu noktaların koordinat düzlemindeki gösterimi aşağıdaki gibidir.
Denklemi \( (x - 3)(x + 5) + (y - 4)(y + 2) = 0 \) olan çemberin merkezini ve yarıçap uzunluğunu bulunuz.
Çözümü GösterDenklemi verilen çemberin genel denklemini yazalım.
\( (x - 3)(x + 5) + (y - 4)(y + 2) = 0 \)
\( x^2 + 2x - 15 + y^2 - 2y - 8 = 0 \)
\( x^2 + y^2 + 2x - 2y - 23 = 0 \)
Genel denklemi \( x^2 + y^2 + Dx + Ey + F = 0 \) şeklinde olan çemberin merkezi ve yarıçap uzunluğu aşağıdaki şekilde bulunur.
\( M(a, b) = M(-\dfrac{D}{2}, -\dfrac{E}{2}) \)
\( r = \dfrac{1}{2}\sqrt{D^2 + E^2 - 4F} \)
Genel denklemden elde edilen katsayıları yukarıdaki eşitliklerde yerine koyalım.
\( D = 2, \quad E = -2, \quad F = -23 \)
\( M(a, b) = M(-\dfrac{2}{2}, -\dfrac{-2}{2}) = M(-1, 1) \)
\( r = \dfrac{1}{2}\sqrt{2^2 + (-2)^2 - 4(-23)} = 5 \)
Çemberin merkezi \( M(-1, 1) \) noktası ve yarıçapı 5 birim olarak bulunur.
\( (x - 3)^2 + (y - 4)^2 = a \) çemberinin çaplarından biri \( [KL] \)'dir.
\( K(5, 2) \) olduğuna göre, \( L \) noktasının koordinatlarını bulunuz.
Çözümü GösterVerilen çemberin merkezi \( M(3, 4) \) noktasıdır.
\( [KL] \) çemberin çaplarından biri olduğuna göre, çemberin merkezi olan \( M \) noktası \( [KL] \) doğru parçasını ortalar.

\( L \) noktasının koordinatlarına \( L(a, b) \) diyelim ve koordinatlarını orta nokta formülünü kullanarak bulalım.
\( (\dfrac{5 + a}{2}, \dfrac{2 + b}{2}) = M(3, 4) \)
\( \dfrac{5 + a}{2} = 3 \)
\( a = 1 \)
\( \dfrac{2 + b}{2} = 4 \)
\( b = 6 \)
\( L(1, 6) \) bulunur.
Genel denklemi \( x^2 + y^2 + ax + by - 56 = 0 \) olan çemberin merkezi \( M(-7, 4) \) noktası olduğuna göre, çemberin yarıçapı kaçtır?
Çözümü GösterMerkez noktasını kullanarak çemberin standart denklemini yazalım.
Çemberin yarıçapına \( r \) diyelim.
\( (x + 7)^2 + (y - 4)^2 = r^2 \)
Bu denklemin açılımını yazalım.
\( x^2 + 14x + 49 + y^2 - 8y + 16 = r^2 \)
\( x^2 + y^2 + 14x - 8y + 65 - r^2 = 0 \)
Elde ettiğimiz denklemi soruda verilen denkleme eşitleyelim.
\( x^2 + y^2 + 14x - 8y + 65 - r^2 = x^2 + y^2 + ax + by - 56 \)
İki denklem aynı çembere ait olduğu için benzer terimlerin katsayıları birbirine eşittir.
\( 65 - r^2 = -56 \)
\( r^2 = 121 \)
Yarıçap değeri negatif olamaz.
\( r = 11 \) bulunur.
\( x^2 + y^2 = 25 \) çemberi üzerinde koordinatları tam sayı olan kaç nokta vardır?
Çözümü GösterVerilen denklemi sağlayan doğal sayı \( x \) ve \( y \) değerleri aşağıdaki gibidir.
\( 5^2 + 0^2 = 25 \)
\( 4^2 + 3^2 = 25 \)
\( 3^2 + 4^2 = 25 \)
\( 0^2 + 5^2 = 25 \)
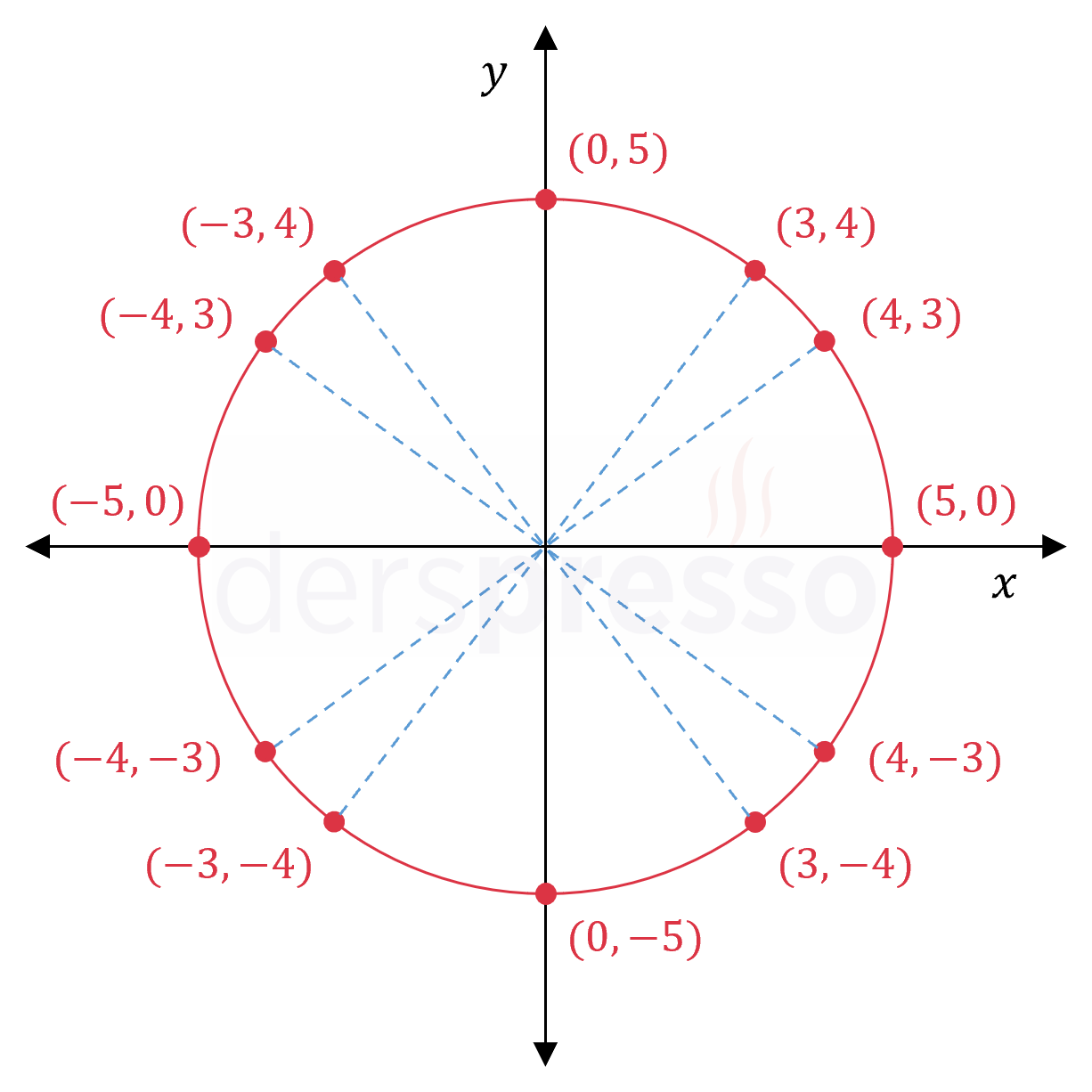
Bu \( (x, y) \) ikililerinin eksenlere göre yansımalarını da dikkate alırsak verilen çember üzerinde koordinatları tam sayı olan 12 nokta bulunur.
(5, 0), (4, 3), (3, 4), (0, 5), (-3, 4), (-4, 3), (-5, 0), (-4, -3), (-3, -4), (0, -5), (3, -4), (4, -3)
\( x^2 + y^2 - 4y = 0 \) çemberinin merkezinden geçen ve \( 2x - y = 1 \) doğrusuna paralel olan doğrunun denklemini bulunuz.
Çözümü GösterGenel denklemi \( x^2 + y^2 + Dx + Ey + F = 0 \) şeklinde olan çemberin merkezi ve yarıçap uzunluğu aşağıdaki gibi bulunur.
\( M(-\dfrac{D}{2}, -\dfrac{E}{2}) = M(-\dfrac{0}{2}, -\dfrac{-4}{2}) = M(0, 2) \)
Çemberin merkezinden geçen ve \( 2x - y = 1 \) doğrusuna paralel olan doğrunun denklemi \( 2x - y + c = 0 \) formundadır.
Bu doğru çemberin merkezinden geçtiğine göre çemberin merkez koordinatları doğru denklemini sağlar.
\( 2(0) - 2 + c = 0 \)
\( c = 2 \)
İstenen doğrunun denklemi aşağıdaki gibidir.
\( 2x - y + 2 = 0 \)
Koordinat düzleminde \( A(-2, 19) \) ve \( B(14, 7) \) noktalarını birleştiren doğru parçası, \( M \) merkezli çemberin de çapıdır.
\( (0, a) \) noktası bu çemberin üzerinde olduğuna göre, \( a \)'nın alabileceği değerler toplamı kaçtır?
Çözümü Göster\( [AB] \) doğru parçası çap olduğu için orta noktası çemberin merkezini verir.
Orta noktanın koordinatları formülünü kullanalım.
\( M(\dfrac{-2 + 14}{2}, \dfrac{19 + 7}{2}) = M(6, 13) \)
Çemberin yarıçapı, merkezi ile üzerindeki herhangi bir nokta arasındaki uzaklığa eşittir.
İki nokta arasındaki uzaklık formülünü kullanalım.
\( \abs{MA} = \sqrt{(6 - (-2))^2 + (13 - 19)^2} \)
\( = \sqrt{64 + 36} = 10 \)
Bu bilgileri kullanarak çemberin standart denklemini yazalım.
\( (x - 6)^2 + (y - 13)^2 = 10^2 \)
\( (0, a) \) noktası çemberin üzerinde olduğuna göre koordinatları denklemi sağlar.
\( (0 - 6)^2 + (a - 13)^2 = 100 \)
\( (a - 13)^2 = 64 \)
\( \abs{a - 13} = 8 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( a - 13 = 8 \)
\( a = 21 \)
Durum 2:
\( a - 13 = -8 \)
\( a = 5 \)
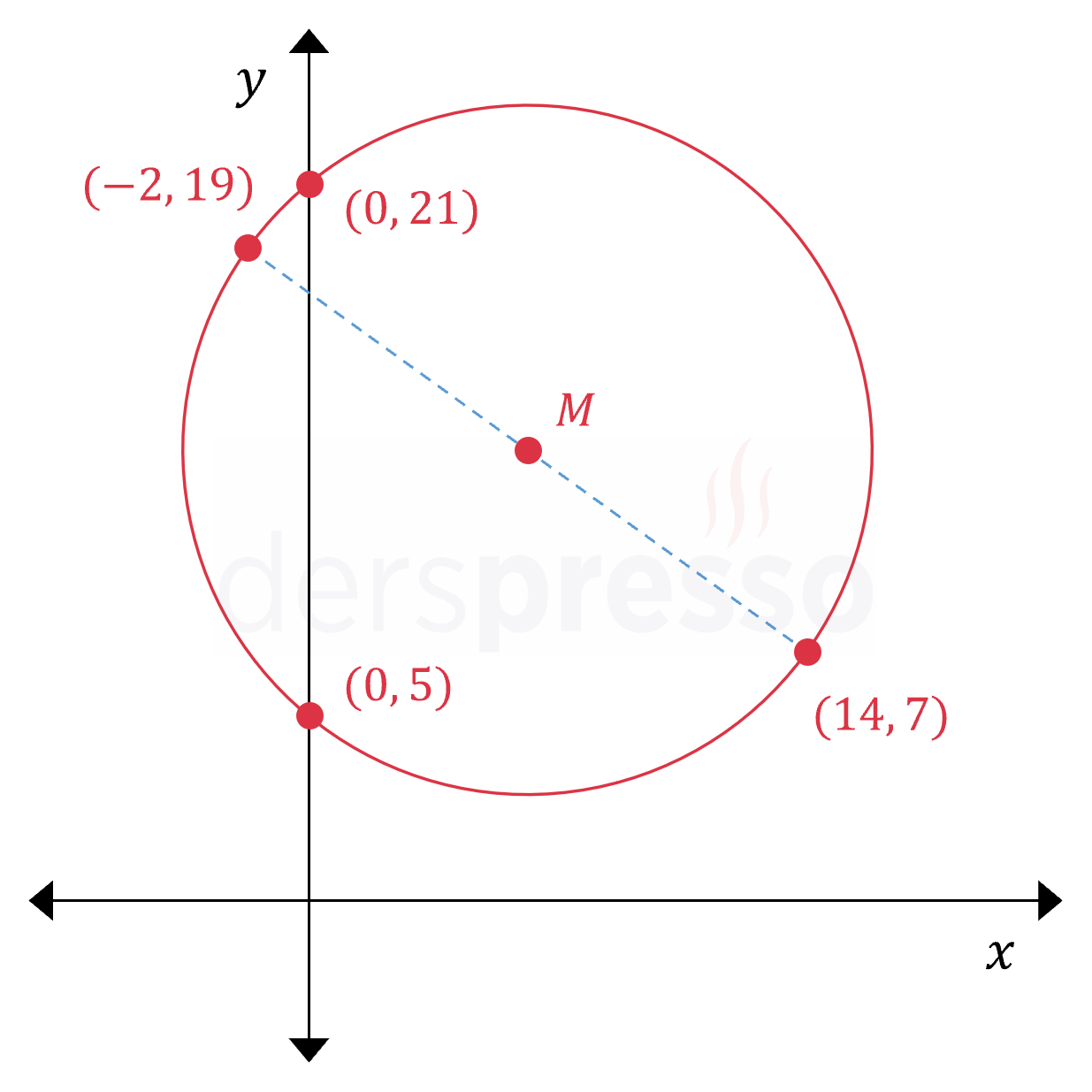
Buna göre \( a \)'nın alabileceği değerler toplamı \( 21 + 5 = 26 \) olarak bulunur.
Soruda verilen ve bulduğumuz noktalar aşağıdaki şekilde gösterilmiştir.
\( A(12, 4) \), \( B(6, -4) \) ve \( C(0, -2) \) noktalarından geçen çemberin genel denklemini bulunuz.
Çözümü GösterÇemberin genel denklemini yazalım.
\( x^2 + y^2 + Dx + Ey + F = 0 \)
Verilen üç nokta da çemberin üzerinde olduğu için koordinatları denklemi sağlar.
Bu noktaların koordinatlarını ayrı ayrı denklemde yerine koyduğumuzda üç bilinmeyenli üç denklem elde ederiz.
\( A(12, 4) \) noktası için:
\( 12^2 + 4^2 + 12D + 4E + F = 0 \)
\( 12D + 4E + F + 160 = 0 \)
\( B(6, -4) \) noktası için:
\( 6^2 + (-4)^2 + 6D - 4E + F = 0 \)
\( 6D - 4E + F + 52 = 0 \)
\( C(0, -2) \) noktası için:
\( 0^2 + (-2)^2 + 0D - 2E + F = 0 \)
\( -2E + F + 4 = 0 \)
Bulduğumuz üç bilinmeyenli üç denklemden oluşan denklem sistemini çözelim.
İkinci denklemin taraflarını 2 ile çarpalım ve birinci denklemden çıkaralım.
\( 12D + 4E + F + 160 = 0 \)
\( 12D - 8E + 2F + 104 = 0 \)
\( 12E - F + 56 = 0 \)
Bulduğumuz denklemi üçüncü denklemle taraf tarafa toplayalım.
\( 12E - F + 56 = 0 \)
\( -2E + F + 4 = 0 \)
\( 10E + 60 = 0 \)
\( E = -6 \)
Bulduğumuz değeri üçüncü denklemde yerine koyarak \( F \)'yi bulalım.
\( -2(-6) + F + 4 = 0 \)
\( F = -16 \)
Bulduğumuz değerleri birinci denklemde yerine koyarak \( D \)'yi bulalım.
\( 12D + 4(-6) + (-16) + 160 = 0 \)
\( D = -10 \)
Buna göre çemberin genel denklemi aşağıdaki gibidir.
\( x^2 + y^2 - 10x - 6y - 16 = 0 \)
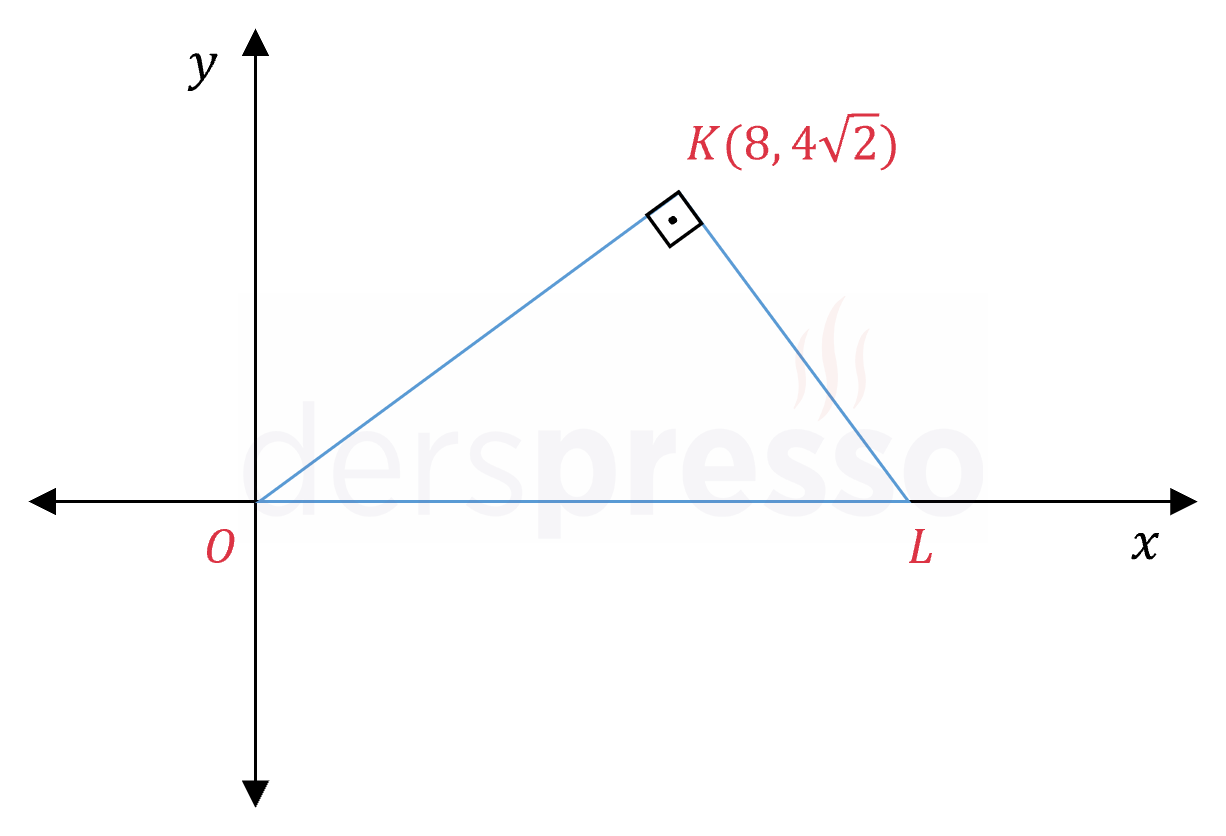
Şekilde verilen \( OKL \) üçgeninin çevrel çemberinin denklemini yazınız.
Çözümü GösterDik açılı üçgenlerde çevrel çemberin merkezi hipotenüsün orta noktasıdır.
Buna göre çevrel çemberin çapı \( [OL] \) olup merkezi \( [OL] \) doğru parçasının orta noktasıdır.
\( \abs{OL} \) değerini bulmak için \( K \) noktasından \( x \) eksenine bir dikme indirelim ve ekseni kestiği noktaya \( N \) diyelim.
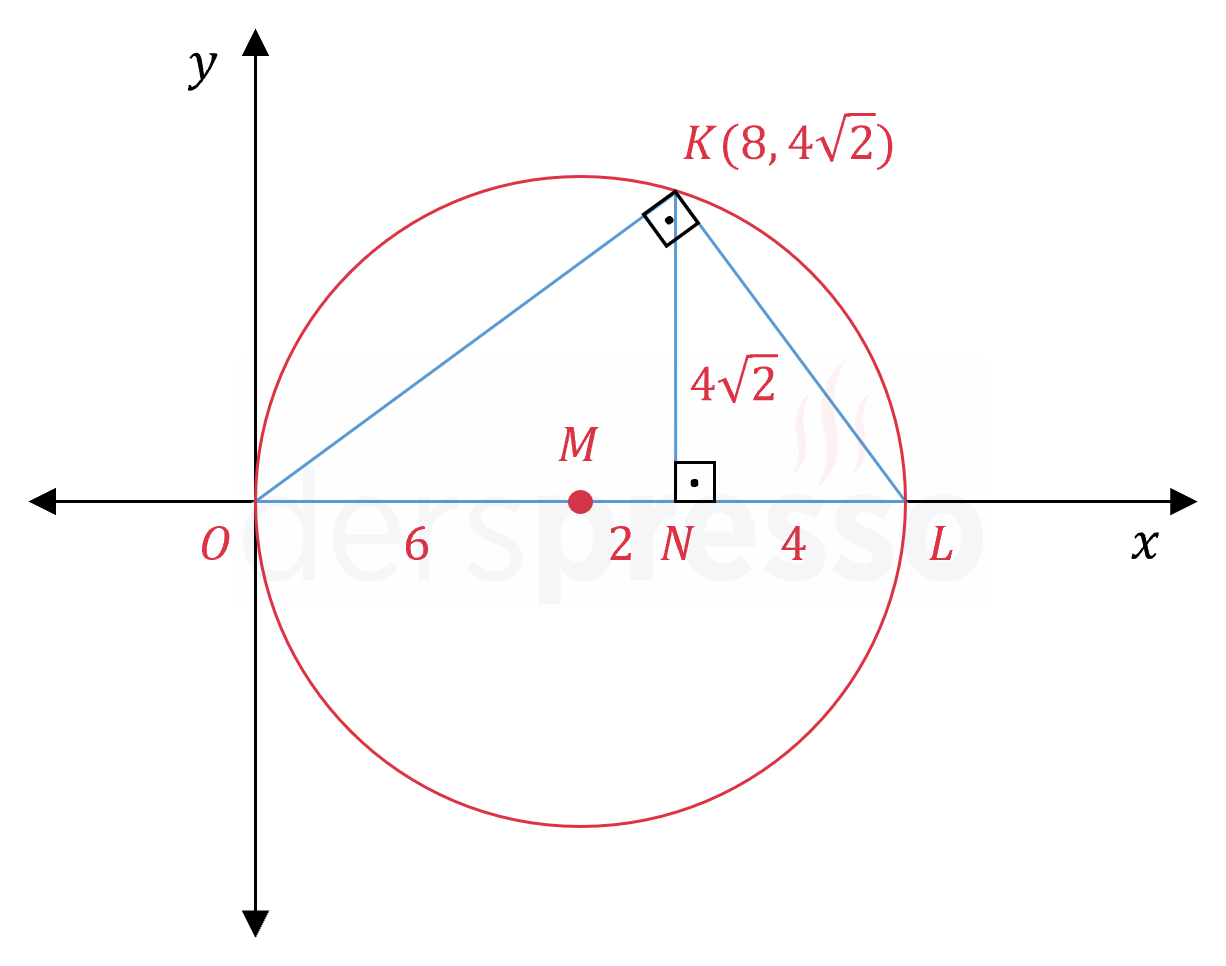
\( OKL \) üçgeninde Öklid bağıntısı kurarak \( \abs{NL} \) değerini bulalım.
\( \abs{KN}^2 = \abs{ON} \cdot \abs{NL} \)
\( (4\sqrt{2})^2 = 8 \cdot \abs{NL} \)
\( \abs{NL} = 4 \)
\( \abs{OL} = 12 \)
Çemberin merkezine \( M \) diyelim.
\( M \) merkezi \( [OL] \) çapının orta noktasıdır.
\( M(6, 0) \)
\( \abs{OM} = \abs{ML} = r = 6 \)
Merkezi \( M(6, 0) \) ve yarıçap uzunluğu 6 birim olan çemberin standart denklemini yazalım.
\( (x - 6)^2 + (y - 0)^2 = 6^2 \)
\( (x - 6)^2 + y^2 = 36 \)
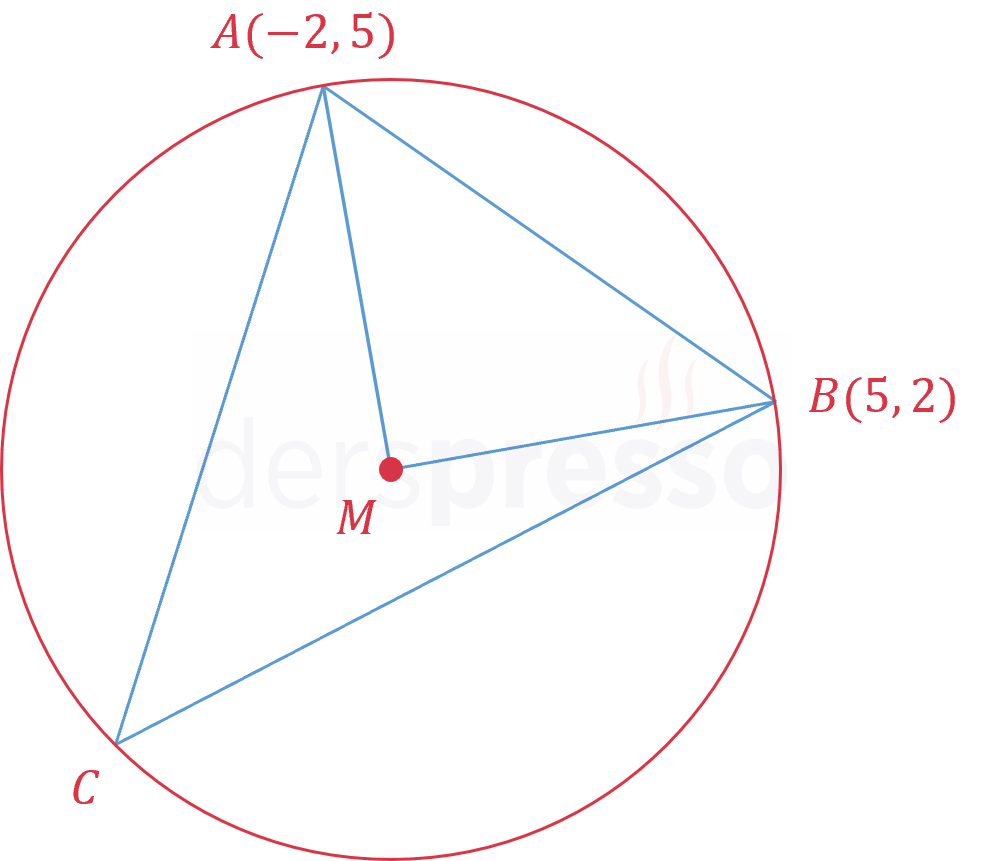
Şekildeki \( x^2 + y^2 = 29 \) çemberinin merkezi \( M \) noktasıdır.
\( A(-2, 5) \) ve \( B(5, 2) \) olduğuna göre, \( m(\widehat{ACB}) \) kaçtır?
Çözümü Göster\( x^2 + y^2 = 29 \) çemberinin merkezi orijindedir.
\( M(0, 0) \)
\( [AM] \) ve \( [BM] \) doğru parçalarının eğimlerine sırasıyla \( m_1 \) ve \( m_2 \) diyelim.
\( m_1 = \dfrac{5 - 0}{-2 - 0} = -\dfrac{5}{2} \)
\( m_2 = \dfrac{2 - 0}{5 - 0} = \dfrac{2}{5} \)
Dik doğruların eğimlerinin çarpımı -1'dir.
\( m_1 \cdot m_2 = -\dfrac{5}{2} \cdot \dfrac{2}{5} = -1 \)
Buna göre \( [AM] \) ve \( [BM] \) doğru parçaları birbirini dik keser.
\( m(\widehat{AMB}) = 90° \)
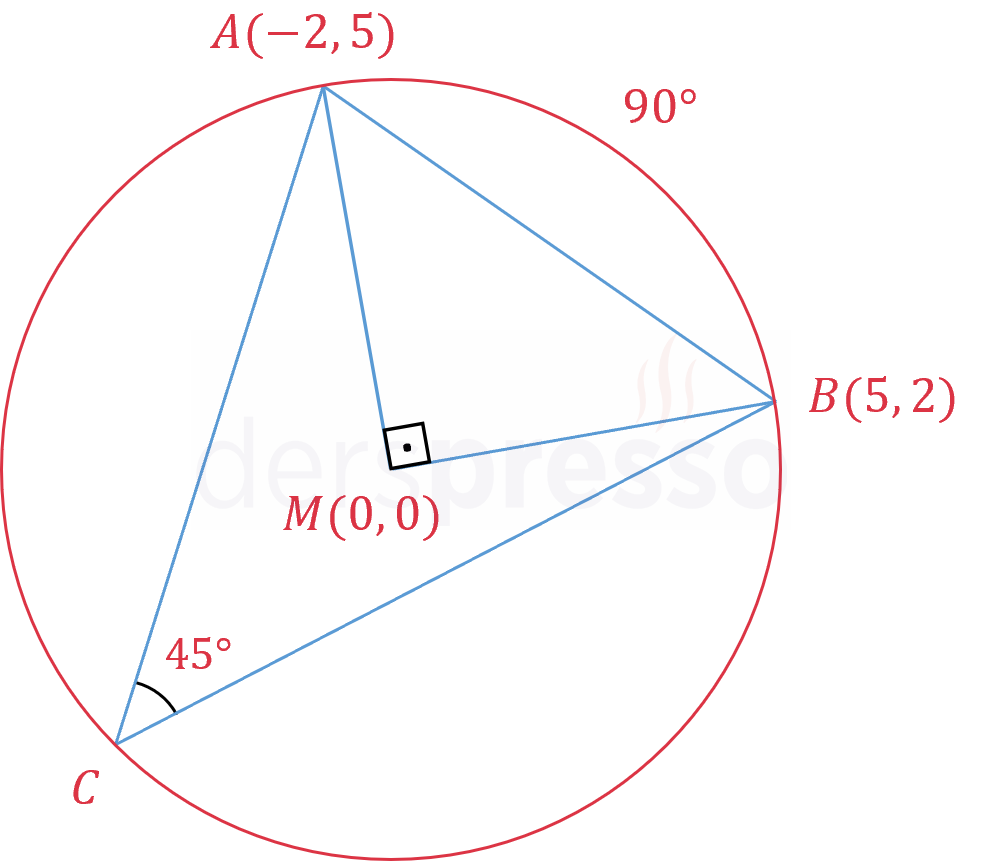
Merkez açının ölçüsü gördüğü yayın ölçüsüne eşittir.
\( m(\overgroup{AB}) = m(\widehat{AMB}) = 90° \)
\( m(\widehat{ACB}) \) çemberin çevre açısı olup ölçüsü gördüğü yayın ölçüsünün yarısına eşittir.
\( m(\overgroup{AB}) = 2m(\widehat{ACB}) = 90° \)
\( m(\widehat{ACB}) = 45° \) bulunur.

\( A(-6, 12) \), \( B(17, -11) \) ve \( C(10, -18) \) aynı çemberin üzerinde üç noktadır.
Buna göre bu çemberin standart denklemini bulunuz.
Çözümü Göster\( [AB] \) ve \( [BC] \) doğru parçalarının eğimini bulalım.
\( m_{AB} = \dfrac{-11 - 12}{17 - (-6)} = -1 \)
\( m_{BC} = \dfrac{-18 - (-11)}{10 - 17} = 1 \)
İki eğimin çarpımı \( -1 \) olduğu için bu iki doğru parçası birbirine diktir.
\( [AB] \perp [BC] \)
\( A \) ve \( C \) noktalarını birleştirelim.
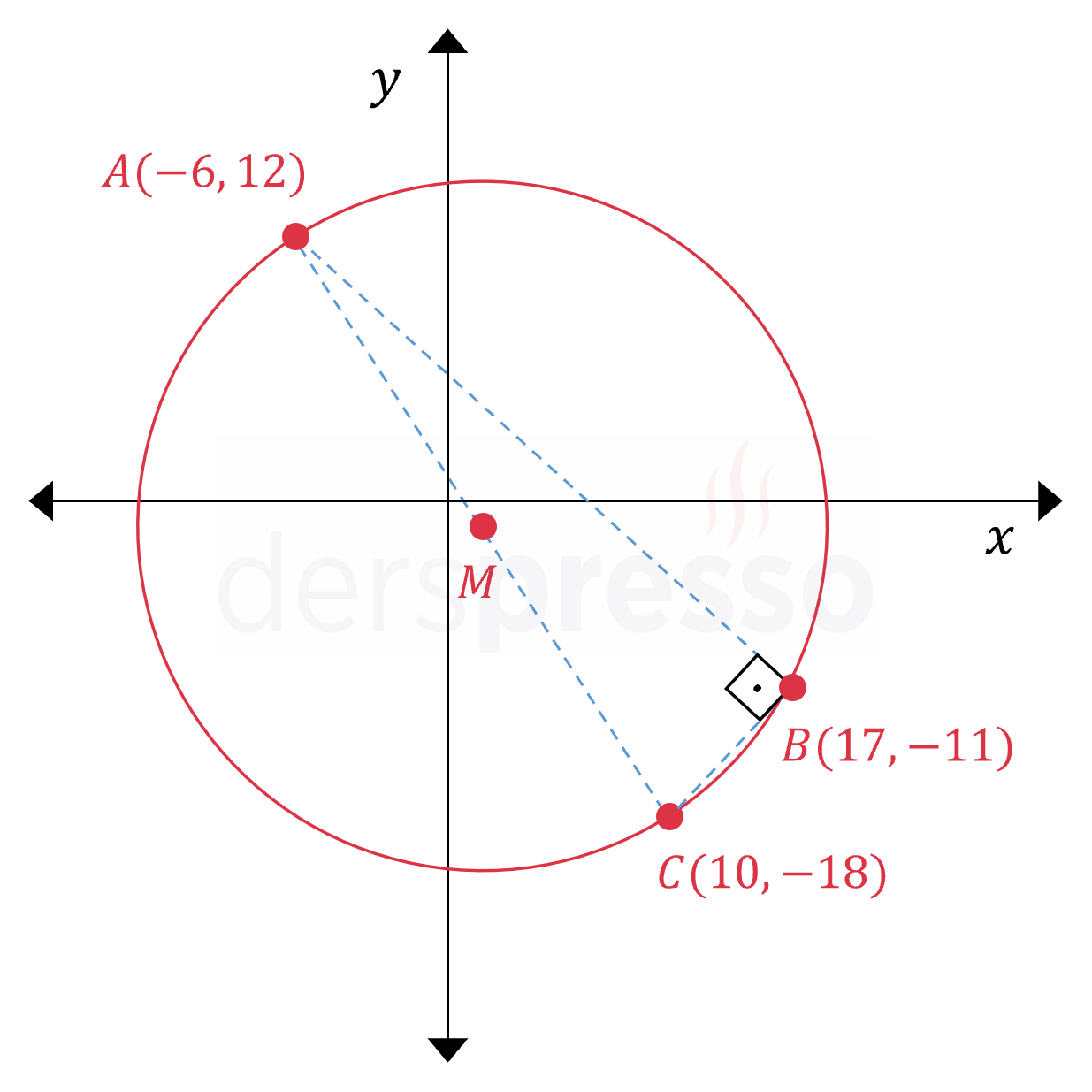
Çapı gören çevre açının ölçüsü \( 90° \)'dir, dolayısıyla \( [AC] \) aynı zamanda çemberin çapıdır.
Çemberin merkezi çapın orta noktasıdır.
Orta noktanın koordinatları formülünü kullanalım.
\( M(\dfrac{-6 + 10}{2}, \dfrac{12 + (-18)}{2}) = M(2, -3) \)
Çemberin yarıçapı, merkezi ile üzerindeki herhangi bir nokta arasındaki uzaklığa eşittir.
İki nokta arasındaki uzaklık formülünü kullanalım.
\( \abs{MC} = \sqrt{(10 - 2)^2 + (-18 - (-3))^2} \)
\( = \sqrt{64 + 225} = 17 \)
Merkez noktası ve yarıçapı bilinen çemberin standart denklemini yazalım.
\( (x - 2)^2 + (y + 3)^2 = 17^2 \)
Koordinat düzlemindeki \( A(4, 7) \) noktası, denklemi \( (x + 8)^2 + (y - 1)^2 = r^2 \) olan çemberin üzerindedir.
Bu çemberin \( A \) noktasındaki normali çemberi başka hangi noktada keser?
Çözümü GösterÇembere bir noktada teğet olan doğruyu o noktada dik kesen doğruya çemberin o noktadaki normali denir.

1. yöntem:
Verilen denklem merkezi \( M(-8, 1) \) noktası olan denkleme aittir.
Çemberin yarıçapı, merkezi ile üzerindeki herhangi bir nokta arasındaki uzaklığa eşittir.
\( \abs{MA} = r = \sqrt{(4 - (-8))^2 + (7 - 1)^2} \)
\( = \sqrt{144 + 36} = 6\sqrt{5} \)
Buna göre çemberin denklemi aşağıdaki gibi bulunur.
\( (x + 8)^2 + (y - 1)^2 = (6\sqrt{5})^2 = 180 \)
Çemberin \( A \) noktasındaki normalini bulmak için iki noktası bilinen doğru denklemi formülünü kullanalım.
\( \dfrac{y - 7}{x - 4} = \dfrac{7 - 1}{4 - (-8)} \)
\( \dfrac{y - 7}{x - 4} = \dfrac{1}{2} \)
\( 2y - 14 = x - 4 \)
\( x = 2y - 10 \)
Bu doğru ile çemberin kesişim noktalarını bulmak için iki denklemi ortak çözelim.
Çemberin denkleminde \( x \) yerine \( 2y - 10 \) yazalım.
\( (2y - 10 + 8)^2 + (y - 1)^2 = 180 \)
\( 4y^2 - 8y + 4 + y^2 - 2y + 1 = 180 \)
\( 5y^2 - 10y - 175 = 0 \)
\( 5(y + 5)(y - 7) = 0 \)
\( y = -5 \) ya da \( y = 7 \)
\( y = 7 \) ordinat değerli nokta soruda verilen \( A \) noktasıdır.
\( x = 2y - 10 \) denkleminde \( y = -5 \) yazarak ikinci noktanın \( x \) koordinatını bulalım.
\( x = 2(-5) - 10 = -20 \)
Normal doğrusunun çemberi kestiği ikinci noktanın koordinatları \( (-20, -5) \) olarak bulunur.
2. yöntem:
Soruyu çemberin merkezinin çap doğrusunun orta noktası olduğu bilgisini kullanarak çözelim.
Normal doğrusunun çemberi kestiği ikinci noktaya \( K(a, b) \) diyelim.
Buna göre çemberin merkezi \( A(4, 7) \) ve \( K(a, b) \) noktalarının orta noktasıdır.
Orta noktanın koordinatları formülünü kullanalım.
\( M(\dfrac{4 + a}{2}, \dfrac{7 + b}{2}) = M(-8, 1) \)
\( \dfrac{4 + a}{2} = -8 \)
\( a = -20 \)
\( \dfrac{7 + b}{2} = 1 \)
\( b = -5 \)
\( K \) noktasının koordinatları \( (-20, -5) \) olarak bulunur.
\( (x + 6)^2 + (y + 3)^2 = 225 \) çemberinin içindeki \( N(4, 2) \) noktasından geçen en kısa kirişin uzunluğu kaç birimdir?
Çözümü GösterStandart denklemi verilen çemberin merkezi \( M(-6, -3) \) noktasıdır ve yarıçapı 15 birimdir.
Çemberin merkezi ile \( N \) noktası arasındaki mesafeyi bulalım.
\( \abs{MN} = \sqrt{(-6 - 4)^2 + (-3 - 2)^2} \)
\( = \sqrt{100 + 25} = 5\sqrt{5} \)
Çemberin bir noktadaki en kısa kirişi ile çemberin çapı dik kesişir ve bu çap kirişi ortalar.
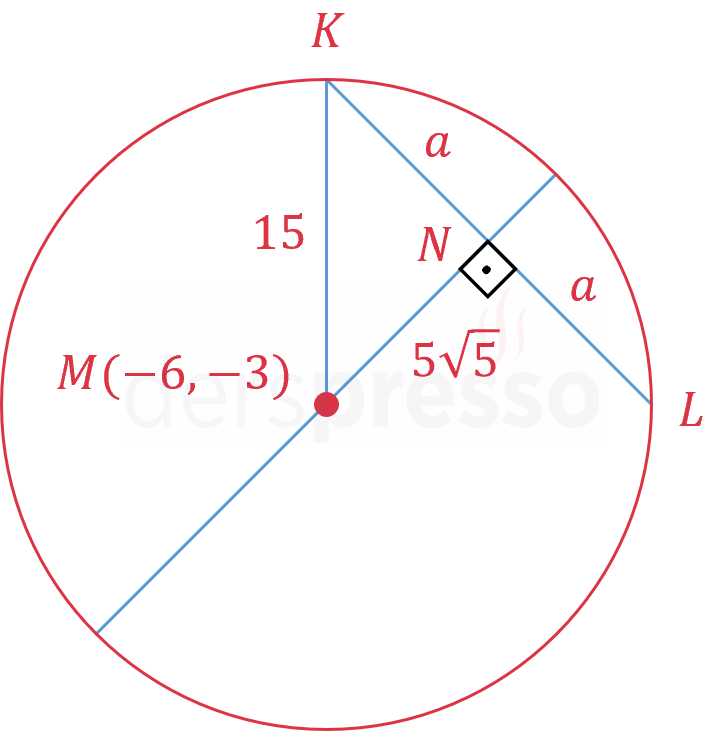
Çemberin en kısa kirişine \( [KL] \) diyelim.
\( \abs{KN} = \abs{LN} = a \) diyelim.
\( [MK] \) yarıçapını çizerek \( MNK \) dik üçgenini oluşturalım ve bu üçgende Pisagor bağlantısını kullanarak \( a \) değerini bulalım.
\( \abs{MK} = r = 15 \)
\( \abs{MK}^2 = \abs{MN}^2 + \abs{KN}^2 \)
\( 15^2 = (5\sqrt{5})^2 + \abs{KN}^2 \)
\( 225 = 125 + \abs{KN}^2 \)
\( \abs{KN} = a = 10 \)
\( \abs{KL} = 2a = 20 \) bulunur.
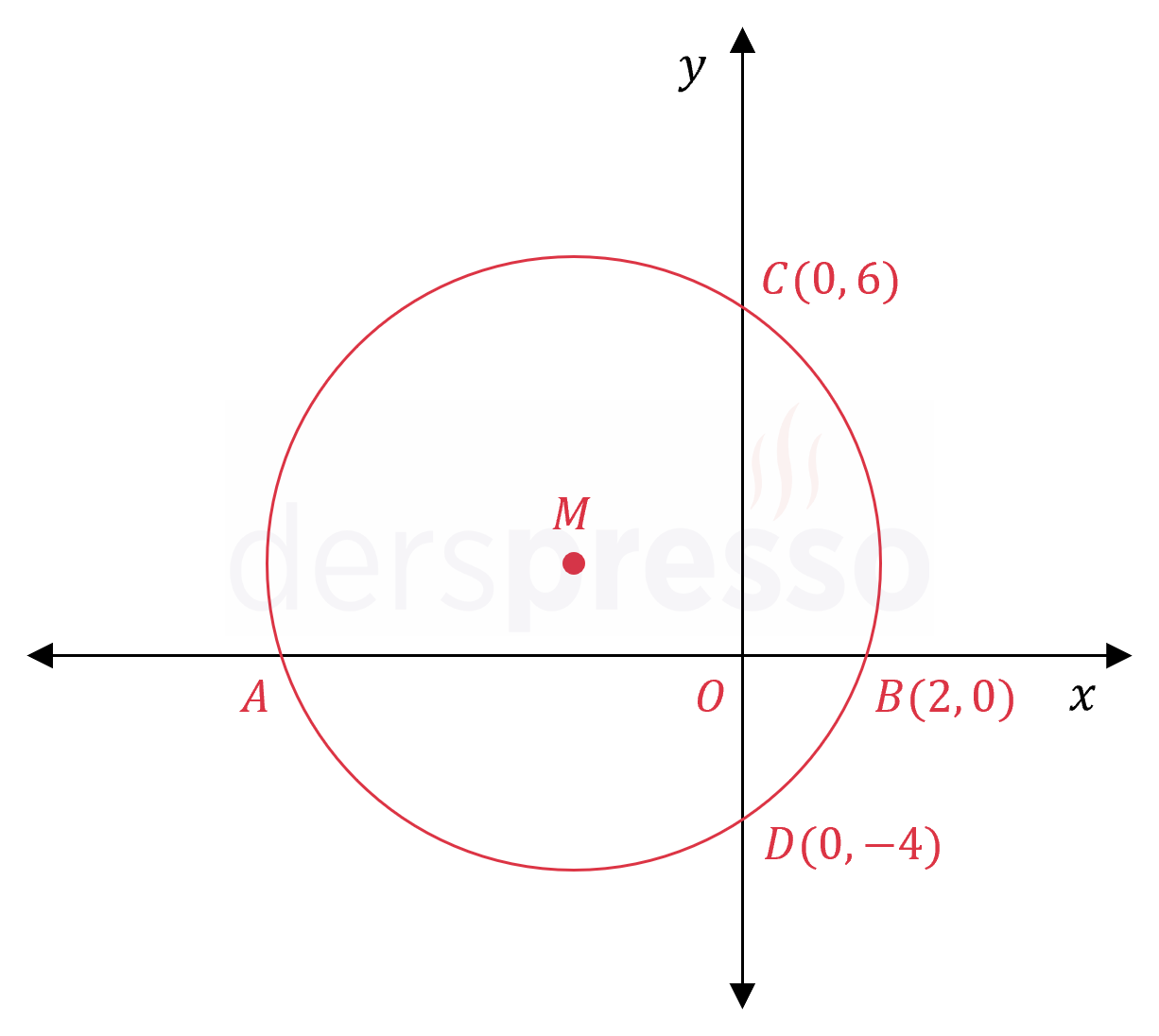
Şekilde verilen \( M \) merkezli çemberin denklemini bulunuz.
Çözümü Göster\( [AB] \) ve \( [CD] \) kirişleri orijinden geçmektedir.
Bir çemberde iki kirişin kesişim noktasının kirişlerde ayırdığı doğru parçalarının uzunluklarının çarpımı birbirine eşittir.
\( \abs{OA} \cdot \abs{OB} = \abs{OC} \cdot \abs{OD} \)
\( \abs{OA} \cdot 2 = 6 \cdot 4 \)
\( \abs{OA} = 12 \)
\( A(-12, 0) \)
Çemberin merkezinden \( [AB] \) ve \( [CD] \) kirişlerine birer dikme indirelim.
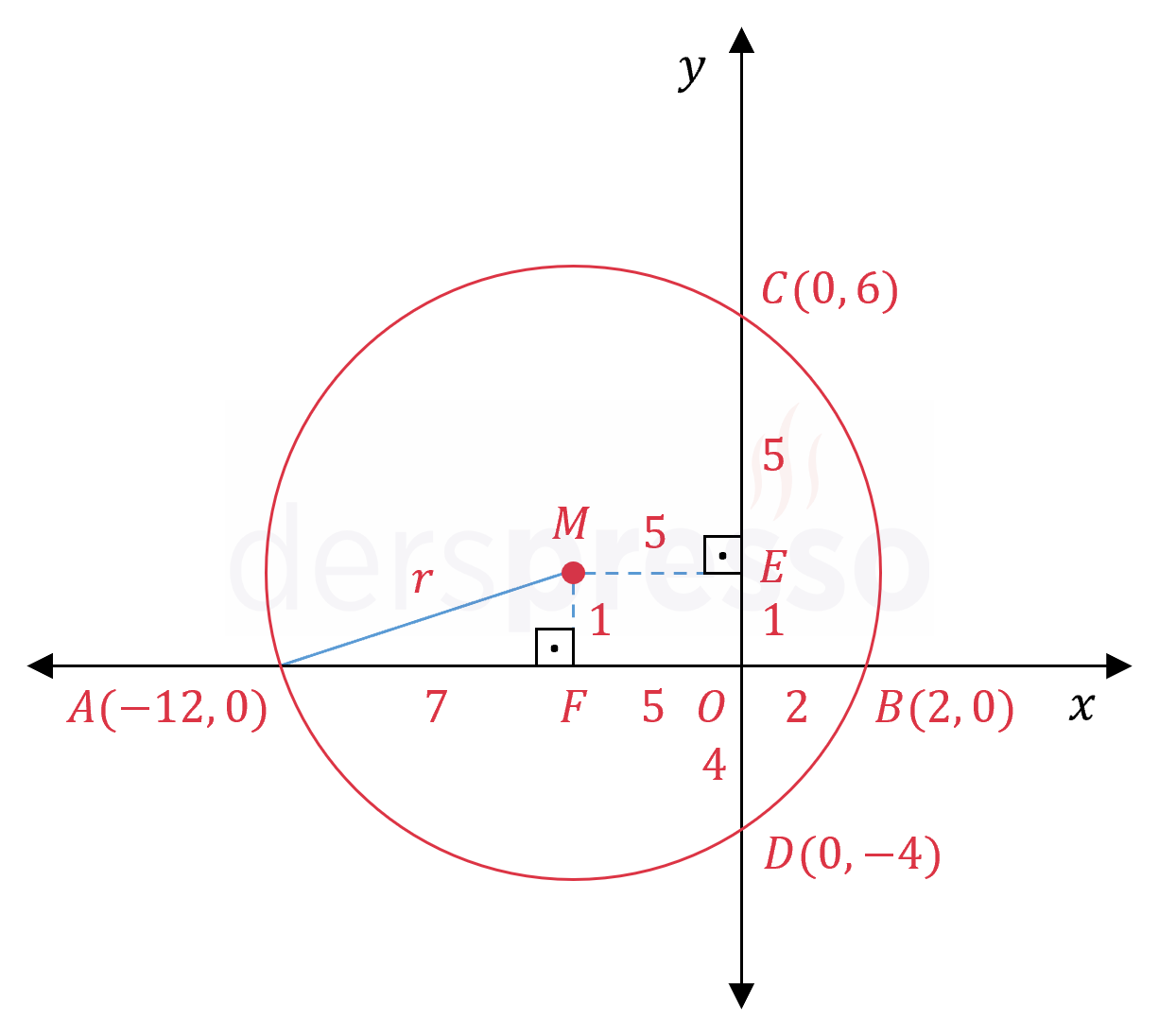
Merkezden kirişlere indirilen dikmeler kirişleri ortalar.
\( \abs{CE} = \abs{DE} = 5 \)
\( \abs{AF} = \abs{BF} = 7 \)
\( \abs{OF} = 5 \)
\( \abs{OE} = 1 \)
Bu uzunlukları kullanarak çemberin merkezinin koordinatlarını yazalım.
\( M(-5, 1) \)
\( [MA] \) yarıçapını çizerek \( MFA \) dik üçgenini oluşturalım ve bu üçgende Pisagor bağıntısını kullanarak çemberin yarıçapını bulalım.
\( \abs{MA}^2 = \abs{MF}^2 + \abs{AF}^2 \)
\( r^2 = 1^2 + 7^2 = 50 \)
Merkezi \( M(a, b) \) noktası ve yarıçapı \( r \) olan çemberin standart denklemi aşağıdaki gibidir.
\( (x - a)^2 + (y - b)^2 = r^2 \)
\( (x + 5)^2 + (y - 1)^2 = 50 \)
\( (n, 2n), (2, 0), (0, 2), (0, 0) \) aynı çember üzerinde bulunan birbirinden farklı noktalardır.
Buna göre \( n \) değeri kaçtır?
Çözümü GösterYöntem 1:
Çemberin genel denklemine \( x^2 + y^2 + Dx + Ey + F = 0 \) diyelim.
Verilen noktalar çemberin üzerinde olduğuna göre koordinatları denklemi sağlar.
\( (0, 0) \) noktasını denklemde yerine koyalım.
\( 0^2 + 0^2 + D(0) + E(0) + F = 0 \)
\( F = 0 \)
\( (2, 0) \) noktasını denklemde yerine koyalım.
\( 2^2 + 0^2 + D(2) + E(0) = 0 \)
\( D = -2 \)
\( (0, 2) \) noktasını denklemde yerine koyalım.
\( 0^2 + 2^2 + D(0) + E(2) = 0 \)
\( E = -2 \)
Buna göre çemberin genel denklemi aşağıdaki gibi bulunur.
\( x^2 + y^2 - 2x - 2y = 0 \)
\( (n, 2n) \) noktasını denklemde yerine koyalım.
\( n^2 + (2n)^2 - 2n - 2(2n) = 0 \)
\( 5n^2 - 6n = 0 \)
\( n(5n - 6) = 0 \)
\( n = 0 \) ya da \( n = \dfrac{6}{5} \)
Soruda verilen noktalar birbirinden farklı noktalar olduğu için \( (n, 2n) = (0, 0) \) olamaz.
\( (n, 2n) = (\dfrac{6}{5}, \dfrac{12}{5}) \)
\( n = \dfrac{6}{5} \) bulunur.
Yöntem 2:
Çemberin merkezine \( M(a, b) \) diyelim.
Verilen noktalar çemberin üzerinde olduğuna göre, her birinin merkeze olan uzaklığı eşit olmalıdır.
\( (0, 0) \) noktasının \( M(a, b) \) noktasına olan uzaklığını bulalım.
\( d_1 = \sqrt{(a - 0)^2 + (b - 0)^2} = \sqrt{a^2 + b^2} \)
\( (2, 0) \) noktasının \( M(a, b) \) noktasına olan uzaklığını bulalım.
\( d_2 = \sqrt{(a - 2)^2 + (b - 0)^2} = \sqrt{(a - 2)^2 + b^2} \)
\( (0, 2) \) noktasının \( M(a, b) \) noktasına olan uzaklığını bulalım.
\( d_3 = \sqrt{(a - 0)^2 + (b - 2)^2} = \sqrt{a^2 + (b - 2)^2} \)
\( (n, 2n) \) noktasının \( M(a, b) \) noktasına olan uzaklığını bulalım.
\( d_4 = \sqrt{(a - n)^2 + (b - 2n)^2} \)
\( d_1, d_2, d_3, d_4 \) uzunluklarının her biri çemberin yarıçapına eşit olup birbirine eşittir. Bu uzunlukları kullanarak \( a \) ve \( b \) değerlerini bulalım.
\( d_1 = d_2 \):
\( \sqrt{a^2 + b^2} = \sqrt{(a - 2)^2 + b^2} \)
\( a^2 + b^2 = (a - 2)^2 + b^2 \)
\( a^2 = a^2 - 4a + 4 \)
\( a = 1 \)
\( d_1 = d_3 \):
\( \sqrt{a^2 + b^2} = \sqrt{a^2 + (b - 2)^2} \)
\( a^2 + b^2 = a^2 + (b - 2)^2 \)
\( b^2 = b^2 - 4b + 4 \)
\( b = 1 \)
\( d_1 = d_4 \):
\( a = b = 1 \) değerlerini kullanarak \( n \) değerini bulalım.
\( \sqrt{a^2 + b^2} = \sqrt{(a - n)^2 + (b - 2n)^2} \)
\( \sqrt{1 + 1} = \sqrt{(1 - n)^2 + (1 - 2n)^2} \)
\( 2 = (1 - n)^2 + (1 - 2n)^2 \)
\( 2 = 1 - 2n + n^2 + 1 - 4n + 4n^2 \)
\( 5n^2 - 6n = 0 \)
\( n(5n - 6) = 0 \)
\( n = 0 \) ya da \( n = \dfrac{6}{5} \)
Soruda verilen noktalar birbirinden farklı noktalar olduğu için \( (n, 2n) = (0, 0) \) olamaz.
\( (n, 2n) = (\dfrac{6}{5}, \dfrac{12}{5}) \)
\( n = \dfrac{6}{5} \) bulunur.
\( (3, 2) \) ve \( (6, -1) \) noktalarından geçen ve merkezi \( x + 3y = 8 \) doğrusu üzerinde bulunan çemberin denklemini bulunuz.
Çözümü GösterÇemberin merkezinin koordinatlarına \( M(a, b) \) diyelim.
Çemberin merkezi \( x + 3y = 8 \) doğrusu üzerinde olduğuna göre, koordinatları doğru denklemini sağlar.
\( a + 3b = 8 \)
\( a = 8 - 3b \)
Buna göre \( M \) noktasının koordinatlarını aşağıdaki şekilde ifade edebiliriz.
\( M(8 - 3b, b) \)
\( M \) noktasının verilen iki noktaya uzaklıkları yarıçapa eşit olduğu için birbirine eşit olmalıdır.
\( \sqrt{(8 - 3b - 3)^2 + (b - 2)^2} = \sqrt{(8 - 3b - 6)^2 + (b - (-1))^2} \)
\( \sqrt{(5 - 3b)^2 + (b - 2)^2} = \sqrt{(2 - 3b)^2 + (b + 1)^2} \)
Eşitliğin taraflarının karesi alalım.
\( (5 - 3b)^2 + (b - 2)^2 = (2 - 3b)^2 + (b + 1)^2 \)
\( 25 - 30b + 9b^2 + b^2 - 4b + 4 = 4 - 12b + 9b^2 + b^2 + 2b + 1 \)
\( 29 - 34b = 5 - 10b \)
\( b = 1 \)
\( b \) değerini kullanarak \( a \) değerini bulalım.
\( a + 3b = 8 \)
\( a = 5 \)
\( M(a, b) = M(5, 1) \)
Çemberin yarıçapını bulmak için verilen birinci noktanın merkeze uzaklığını bulalım.
\( r = \sqrt{(5 - 3)^2 + (1 - 2)^2} = \sqrt{5} \)
Merkezi \( M(a, b) \) noktası ve yarıçapı \( r \) olan çemberin standart denklemi aşağıdaki gibidir.
\( (x - a)^2 + (y - b)^2 = r^2 \)
\( (x - 5)^2 + (y - 1)^2 = (\sqrt{5})^2 = 5 \)
Denklemi \( x^2 + y^2 - 4x + 6y - 3 = 0 \) olan çemberin orta noktası \( A(1, -1) \) olan kirişinden geçen doğrunun denklemini bulunuz.
Çözümü GösterGenel denklemi \( x^2 + y^2 + Dx + Ey + F = 0 \) şeklinde olan çemberin merkezi aşağıdaki şekilde bulunur.
\( M(-\dfrac{D}{2}, -\dfrac{E}{2}) = M(-\dfrac{-4}{2}, -\dfrac{6}{2}) = M(2, -3) \)
Çemberin merkezinden kirişe çizilen dikme kirişi ortalar, dolayısıyla merkezden kirişe çizilen dikme kirişi \( A(1, -1) \) noktasında keser.
\( [MA] \) doğrusunun eğimini iki noktası bilinen doğrunun eğimi formülü ile bulalım.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( m_{MA} = \dfrac{-3 - (-1)}{2 - 1} = -2 \)
Kirişten geçen doğruya \( d \) diyelim.
Dik kesişen doğruların eğimleri çarpımı -1'dir.
\( m_d \cdot m_{MA} = -1 \)
\( m_d \cdot -2 = -1 \)
\( m_d = \dfrac{1}{2} \)
\( d \) doğrusunun denklemini bir noktası ve eğimi bilinen doğru denklemini kullanarak bulalım.
\( y - y_0 = m(x - x_0) \)
\( y - (-1) = \dfrac{1}{2}(x - 1) \)
\( y + 1 = \dfrac{1}{2}(x - 1) \)
\( 2y - x + 3 = 0 \) bulunur.
\( x^2 + y^2 \lt 36 \) koşulunu sağlayan ve koordinatları tam sayı olan kaç tane \( (x, y) \) noktası vardır?
Çözümü GösterVerilen eşitsizliği sağlayan \( (x, y) \) noktaları, merkezi orijinde olan ve yarıçap uzunluğu 6 birim olan çemberin iç bölgesinde yer alan noktalardır.
Bu eşitsizliği sağlayan en küçük ve en büyük \( x \) ve \( y \) değerleri \( \pm 5 \) olur.
Bu nedenle \( x \) ve \( y \) değerleri \( \{-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5\} \) kümesinden seçilebilir.
Bu kümeden \( (x, y) \) ikilileri \( 11 \cdot 11 = 121 \) farklı şekilde seçilebilir.
Ancak aşağıdaki 12 ikili için \( (x, y) \) noktaları çemberin dışında kalır ve \( x^2 + y^2 \lt 36 \) koşulunu sağlamaz.
\( (\pm 5, \pm 5), (\pm 5, \pm 4), (\pm 4, \pm 5) \)

Buna göre istenen koşulları sağlayan \( 121 - 12 = 109 \) tane \( (x, y) \) noktası vardır.