Cebirsel İfade Tanımı
Temel Kavramlar
Değişken
Bir matematiksel ifadede farklı değerler alabilen sembollere değişken denir. Değişkenler genellikle \( x \), \( y \), \( z \), \( t \), \( u \), \( v \) gibi alfabenin sonundaki harflerle gösterilirler.
Aşağıda kırmızı ile işaretli semboller birer değişkendir.
\( 2\textcolor{red}{x}^2 - 5\textcolor{red}{xy} - 3\textcolor{red}{y}^2 \)
\( \textcolor{red}{A} = \pi \textcolor{red}{r}^2 \)
\( \textcolor{red}{y} = 2\textcolor{red}{x}^2 - 3\textcolor{red}{x} + 5 \)
Sayılarının çok olduğu durumlarda değişkenler \( x_1, x_2, \ldots, x_n \) şeklinde alt simgelerle isimlendirilebilirler.
Herhangi bir değişken için kullanılabilen \( x , y, z \) sembollerine ek olarak aşağıdaki semboller sıklıkla belirtilen anlamda kullanılırlar.
| Sembol | Anlam |
|---|---|
| \( t \) | Zaman |
| \( v \) | Hız |
| \( r \) | Çemberin yarıçapı |
| \( h \) | Bir geometrik şeklin yüksekliği |
| \( z \) | Karmaşık sayı |
| \( \alpha, \beta, \theta \) | Açı ölçüsü |
| \( m, n, p, q \) | Tam sayı büyüklük |
| \( \epsilon, \delta \) | Çok küçük değerli değişkenler |
Bir denklem ya da eşitsizlikte sınırlı sayıda değer alabilen ve alabileceği değerleri bulmaya çalıştığımız değişkenlere bilinmeyen denir.
Katsayı
Bir matematiksel ifadede değişkenlerin önündeki çarpanlara katsayı denir.
Katsayıların değeri biliniyorsa ifadelerde birer sayı olarak bulunurlar, bilinmiyorsa genellikle \( a \), \( b \), \( c \), \( d \) gibi alfabenin başındaki harflerle gösterilirler.
Aşağıda kırmızı ile işaretli semboller birer katsayıdır.
\( \textcolor{red}{2}x^2 \textcolor{red}{- 5}xy \textcolor{red}{- 3}y^2 \)
\( A = \textcolor{red}{\pi}r^2 \)
\( y = \textcolor{red}{a}x^2 + \textcolor{red}{b}x + \textcolor{red}{c} \)
Sayısal İfadeler
Sadece sayılardan ve işlemlerden oluşan matematiksel ifadelere sayısal ifade denir.
\( 2 \cdot 3^2 + 3\sqrt{2} \)
\( 3^2 \cdot (5! - 1) \)
Sayısal ifadelerde işlem sırasını belirlemek için parantez kullanılabilir.
Cebirsel İfadeler
Sayılardan, işlemlerden ve en az bir değişkenden oluşan matematiksel ifadelere cebirsel ifade denir.
\( 2x + 3 \)
\( x^2 - 3xy + 2y^2 \)
\( \sqrt{x - 2} - \dfrac{2}{x} \)
Cebirsel ifadeler eşitlik (\( = \)) ya da eşitsizlik (\( \lt, \le, \gt, \ge, \ne \)) sembolleri içermezler, bu sembollerin eklenmesiyle birlikte denklem ve eşitsizlikleri oluştururlar.
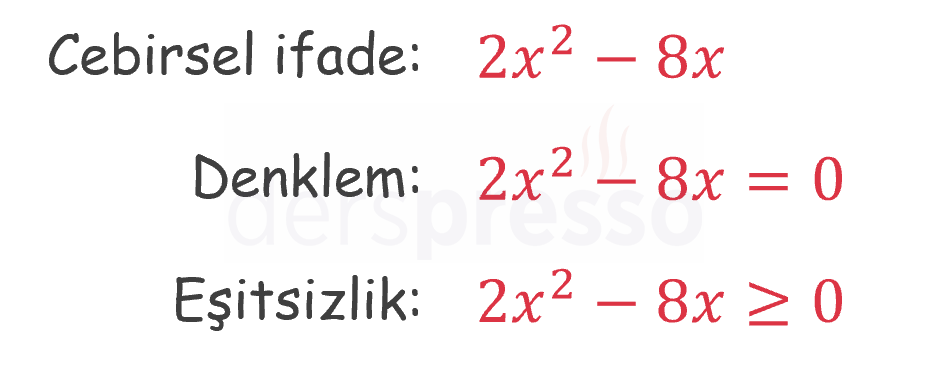
Bir cebirsel ifadenin toplama ve çıkarma sembolleri ile ayrılmış kısımlarına terim denir. Aşağıda dört terimli bir cebirsel ifadenin terimleri gösterilmiştir.
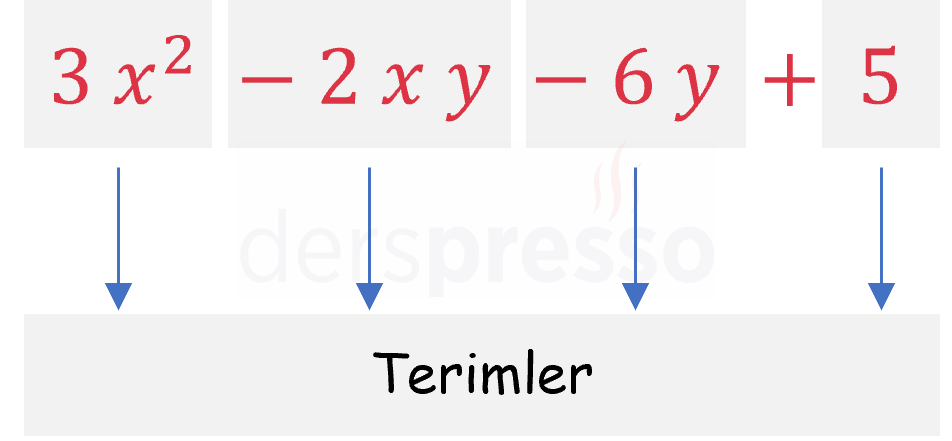
Her terim bir katsayı ile bir ya da daha fazla sayıda değişkenin çarpımından oluşur. Bir terim sadece değişkenlerden oluşuyorsa katsayısı 1 olarak kabul edilir. Bir terimin önünde negatif işareti varsa bu işaret katsayıya dahil edilir ve katsayıyı negatif yapar.
Bir terim iki ya da daha fazla katsayı ya da değişkenden oluşuyorsa, bu katsayı ve değişkenlerin her biri o terimin birer çarpanıdır. Örneğin \( 6xy \) teriminin çarpanları \( 6 \), \( x \) ve \( y \)'dir.
Sadece katsayıdan oluşan ve bir değişken içermeyen terime sabit terim denir. Sabit terim genellikle cebirsel ifadenin son terimi olarak yazılır. Sabit terimler değişkenlerin üssünün sıfır olduğu (\( x^0, x^0y^0 \) gibi) terimin katsayısı olarak da düşünülebilir.
Aşağıda kırmızı ile işaretli sembol bir sabit terimdir.
\( x^2 - 4x + \textcolor{red}{5} \)
Bir cebirsel ifadenin tüm bileşenleri aşağıdaki şekilde gösterilmiştir.
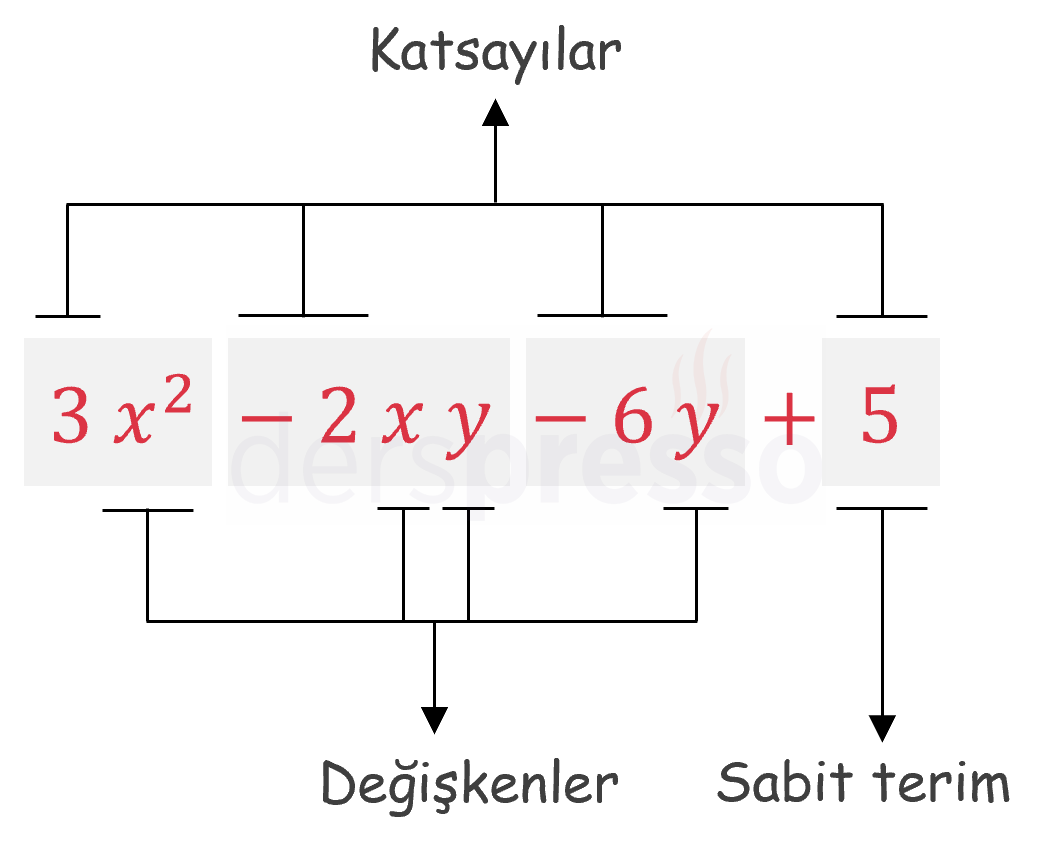
Bir terimin çarpanları arasında çarpı (\( \times \)) ya da nokta (\( \cdot \)) sembolü kullanılması matematiksel açıdan doğru olsa da, çarpı sembolü \( x \) değişkeni ile, nokta sembolü de bindelik ayracı ile karıştırılabileceği için çoğu zaman hiçbir sembol kullanılmaması tercih edilir.
\( 4 \times x \times y = 4 \cdot x \cdot y = 4xy \)
Benzer Terim
Bir cebirsel ifadede değişkenleri ve değişkenlerinin üsleri aynı olan ya da aynı biçime getirilebilen terimlere benzer terim denir. Bir cebirsel ifadede benzer terimler gruplanıp katsayıları arasında toplama ve çıkarma işlemleri yapılarak ifadenin terim sayısı azaltılabilir.
Aşağıda her satırda verilen terimler kendi aralarında benzerdir.
Sabit terimler: \( 2, -\sqrt{2}, \pi \)
\( x, -5x, \sqrt{3}x \)
\( \sqrt{x}, \sqrt{3x} = \sqrt{3}\sqrt{x}, 4x^{\frac{1}{2}} = 4\sqrt{x} \)
\( xy^2, 2y^2x, -yxy \)
Aşağıdaki terim ikilileri benzer değildir.
\( x, xy \): Değişkenler farklı
\( xy, xy^2 \): Değişkenler aynı, ancak kuvvetleri farklı
Bir Cebirsel İfadenin Değerini Hesaplama
Bir cebirsel ifadenin değeri, ifadedeki her bir değişkene birer değer verildiğinde ifadenin hesaplanan değeridir.
Cebirsel ifade:
\( x^2 + 4xy - 6 \)
Değişken değerleri:
\( x = 4, \quad y = 2 \)
Cebirsel ifadenin değeri:
\( 4^2 + 4 \cdot 4 \cdot 2 - 6 \)
\( = 16 + 32 - 6 = 42 \)