Bernoulli Denklemleri
Aşağıdaki formda olan ya da bu formda yazılabilen birinci mertebeden denklemlere Bernoulli denklemi denir.
\( n \in \mathbb{R} - \{0, 1\} \) olmak üzere,
\( \dfrac{dy}{dx} + p(x)y = q(x)y^n \)
\( \dfrac{dy}{dx} + 3y = e^xy^3 \)
\( \dfrac{dy}{dx} + xy = x^2\sqrt{y} \)
\( n = 0 \) ya da \( n = 1 \) olduğunda denklem birinci mertebeden bir lineer denklem olur.
\( n = 0 \) için:
\( y' + y\cos{x} = xy^0 \)
\( y' + y\cos{x} = x \)
\( n = 1 \) için:
\( y' + 3xy = xy^1 \)
\( y' + 2xy = 0 \)
Bernoulli denklemlerinin birinci mertebeden lineer denklemlerden farkı, eşitliğin sağ tarafının bir çarpan olarak \( y \) değişkeninin bir reel sayı kuvvetini içermesi, dolayısıyla denklemin lineer olmamasıdır.
Bernoulli denklemleri \( z = y^{1-n} \) şeklinde değişken değiştirildiğinde birinci mertebeden bir lineer denkleme dönüşür ve \( z \) değişkeni için çözülür.
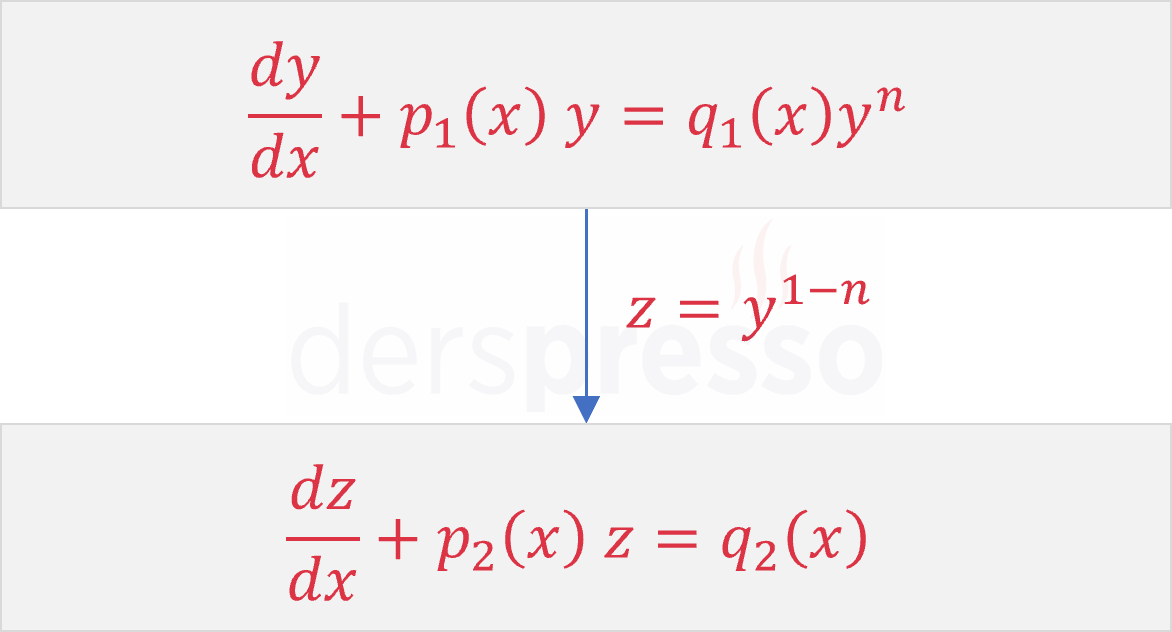
\( n \gt 0 \) olan tüm Bernoulli denklemlerinde \( y = 0 \) denklemin bir sabit çözümü olur.
\( n \gt 0 \) ise,
\( \dfrac{d(0)}{dx} + p(x)(0) = q(x)(0)^n \)
\( 0 + 0 = 0 \)
Bernoulli denklemleri aşağıdaki yöntemle çözülür.
Adım 1: Denklemin formu
Verilen denklem aşağıdaki forma getirilir.
\( \dfrac{dy}{dx} + p_1(x)y = q_1(x)y^n \)
Denklem bu formda değilse ve bu forma getirilemiyorsa bir Bernoulli denklemi değildir, bu durumda denklemi çözmek için farklı bir yöntem kullanılmalıdır.
Adım 2: Değişken değiştirme
Aşağıdaki şekilde bir \( z \) değişkeni tanımlanır ve türevi (\( \frac{dz}{dx} \)) alınır.
\( z = y^{1-n} \)
Denklemdeki \( y \) ve \( \frac{dy}{dx} \) ifadeleri yerine \( z \) ve \( \frac{dz}{dx} \) karşılıkları yazılarak değişken değiştirme uygulanır.
Adım 3: Lineer denklemin çözümü
Değişken değiştirme sonucunda denklem birinci mertebeden bir lineer denkleme dönüşür. Lineer denklem aşağıdaki standart forma getirilir ve integral çarpanı bulunarak çözülür.
\( \dfrac{dz}{dx} + p_2(x)z = q_2(x) \)
Adım 4: Genel çözümün bulunması
Bulunan \( z \) değişkeni cinsinden genel çözüm \( y \) değişkeni cinsinden yazılır.
Adım 5: Başlangıç koşulları
Denklem için başlangıç koşulları verildiyse genel çözümde yerine konarak keyfi sabitler ve denklemin özel çözümü bulunur.
Bernoulli denklemlerinin çözümünü bir örnek üzerinde gösterelim.
\( \dfrac{dy}{dx} + y = 2y^3 \)
denkleminin genel çözümünü bulalım.
Verilen denklem \( n = 3 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-3} = \dfrac{1}{y^2} \)
\( z \) değişkeninin türevini alalım.
\( \dfrac{dz}{dx} = -\dfrac{2}{y^3}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = -\dfrac{y^3}{2}\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım.
\( -\dfrac{y^3}{2}\dfrac{dz}{dx} + y = 2y^3 \)
Denklemi standart forma getirelim.
\( \dfrac{dz}{dx} - \dfrac{2}{y^2} = -4 \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım (\( y^2 = \frac{1}{z} \)).
\( \dfrac{dz}{dx} - 2z = -4 \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {-2dx}} \)
\( = e^{-2x} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( e^{-2x}\dfrac{dz}{dx} - 2e^{-2x}z = -4e^{-2x} \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}(e^{-2x}z) = -4e^{-2x} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( e^{-2x}z + C_1 = \displaystyle\int {-4e^{-2x}\ dx} \)
\( e^{-2x}z = 2e^{-2x} + C \)
\( z = 2 + Ce^{2x} \)
\( z = \frac{1}{y^2} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y^2} = 2 + Ce^{2x} \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y^2 = \dfrac{1}{2 + Ce^{2x}} \)
\( \dfrac{dy}{dx} - \dfrac{y}{5} = e^{2x}y^6 \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterVerilen denklem \( n = 6 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-6} = \dfrac{1}{y^5} \)
\( \dfrac{dz}{dx} = -\dfrac{5}{y^6}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = -\dfrac{y^6}{5}\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( -\dfrac{y^6}{5}\dfrac{dz}{dx} - \dfrac{y}{5} = e^{2x}y^6 \)
\( \dfrac{dz}{dx} + \dfrac{1}{y^5} = -5e^{2x} \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dx} + z = -5e^{2x} \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {1\ dx}} \)
\( = e^x \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( e^x\dfrac{dz}{dx} + e^xz = -5e^{3x} \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}(e^xz) = -5e^{3x} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}(e^xz)\ dx} = \displaystyle\int {-5e^{3x}\ dx} \)
\( e^xz = -\dfrac{5e^{3x}}{3} + C_2 \)
\( z = C_2e^{-x} - \dfrac{5e^{2x}}{3} \)
\( z = \frac{1}{y^5} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y^5} = C_2e^{-x} - \dfrac{5e^{2x}}{3} \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y^5 = \dfrac{3}{Ce^{-x} - 5e^{2x}} \)
\( x \gt 0 \) olmak üzere,
\( xy\dfrac{dy}{dx} + 2y^2 = 6x^2 \)
\( y(1) = 4 \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( \dfrac{dy}{dx} + \dfrac{2y}{x} = \dfrac{6x}{y} \)
Verilen denklem \( n = -1 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1 - (-1)} = y^2 \)
\( \dfrac{dz}{dx} = 2y\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = \dfrac{1}{2y}\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( \dfrac{1}{2y}\dfrac{dz}{dx} + \dfrac{2y}{x} = \dfrac{6x}{y} \)
\( \dfrac{dz}{dx} + \dfrac{4y^2}{x} = 12x \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dx} + \dfrac{4}{x}z = 12x \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {\frac{4}{x}\ dx}} \)
\( = e^{4\ln{\abs{x}}} \)
\( = e^{\ln{x^4}} \)
\( = x^4 \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( x^4\dfrac{dz}{dx} + 4x^3z = 12x^5 \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}(x^4z) = 12x^5 \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}(x^4z)\ dx} = \displaystyle\int {12x^5\ dx} \)
\( x^4z = 2x^6 + C \)
\( z = 2x^2 + \dfrac{C}{x^4} \)
\( z = y^2 \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( y^2 = 2x^2 + \dfrac{C}{x^4} \)
\( y(1) = 4 \) başlangıç değerini denklemde yerine koyalım.
\( 4^2 = 2(1)^2 + \dfrac{C}{1^4} \)
\( C = 14 \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( y^2 = 2x^2 + \dfrac{14}{x^4} \)
\( t \gt 0 \) olmak üzere,
\( y' + \dfrac{3y}{t} = 2ty^4 \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( \dfrac{dy}{dt} + \dfrac{3y}{t} = 2ty^4 \)
Verilen denklem \( n = 4 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-4} = \dfrac{1}{y^3} \)
\( \dfrac{dz}{dt} = -\dfrac{3}{y^4}\dfrac{dy}{dt} \)
\( \Longrightarrow \dfrac{dy}{dt} = -\dfrac{y^4}{3}\dfrac{dz}{dt} \)
Denklemdeki \( \frac{dy}{dt} \) ifadesi yerine \( \frac{dz}{dt} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( -\dfrac{y^4}{3}\dfrac{dz}{dt} + \dfrac{3y}{t} = 2ty^4 \)
\( \dfrac{dz}{dt} - \dfrac{9}{ty^3} = -6t \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dt} - \dfrac{9}{t}z = -6t \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(t) = e^{\int {-\frac{9}{t}\ dt}} \)
\( = e^{-9\ln{\abs{t}}} \)
\( = e^{\ln{t^{-9}}} \)
\( = \dfrac{1}{t^9} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( \dfrac{1}{t^9}\dfrac{dz}{dt} - \dfrac{9}{t^{10}}z = -\dfrac{6}{t^8} \)
Bu eşitliğin sol tarafı, \( \mu(t)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dt}\left( \dfrac{z}{t^9} \right) = -\dfrac{6}{t^8} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dt}\left( \dfrac{z}{t^9} \right)\ dt} = \displaystyle\int {-\dfrac{6}{t^8}\ dt} \)
\( \dfrac{z}{t^9} = \dfrac{6}{7t^7} + C \)
\( z = \dfrac{6t^2}{7} + Ct^9 \)
\( z = \frac{1}{y^3} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y^3} = \dfrac{6t^2 + 7Ct^9}{7} \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y^3 = \dfrac{7}{6t^2 + 7Ct^9} \)
\( t \gt 0 \) olmak üzere,
\( \dfrac{dx}{dt} - \dfrac{2x}{t} = \dfrac{t^2}{3x^2} \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterVerilen denklem \( n = -2 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = x^{1-(-2)} = x^3 \)
\( \dfrac{dz}{dt} = 3x^2\dfrac{dx}{dt} \)
\( \Longrightarrow \dfrac{dx}{dt} = \dfrac{1}{3x^2}\dfrac{dz}{dt} \)
Denklemdeki \( \frac{dx}{dt} \) ifadesi yerine \( \frac{dz}{dt} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( \dfrac{1}{3x^2}\dfrac{dz}{dt} - \dfrac{2x}{t} = \dfrac{t^2}{3x^2} \)
\( \dfrac{dz}{dt} - \dfrac{6x^3}{t} = t^2 \)
Denklemdeki \( x \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dt} - \dfrac{6}{t}z = t^2 \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(t) = e^{\int {-\frac{6}{t}\ dt}} \)
\( = e^{-6\ln{\abs{t}}} \)
\( = e^{\ln{t^{-6}}} \)
\( = \dfrac{1}{t^6} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( \dfrac{1}{t^6}\dfrac{dz}{dt} - \dfrac{6}{t^7}z = \dfrac{1}{t^4} \)
Bu eşitliğin sol tarafı, \( \mu(t)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dt}\left( \dfrac{z}{t^6} \right) = \dfrac{1}{t^4} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dt}\left( \dfrac{z}{t^6} \right)\ dt} = \displaystyle\int {\dfrac{1}{t^4}\ dt} \)
\( \dfrac{z}{t^6} = -\dfrac{1}{3t^3} + C \)
\( z = Ct^6 - \dfrac{t^3}{3} \)
\( z = x^3 \) eşitliğini kullanarak denklemi \( x \) cinsinden yazalım.
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( x^3 = Ct^6 - \dfrac{t^3}{3} \)
\( t \gt 0 \) olmak üzere,
\( y' + \dfrac{2y}{t^2} = \dfrac{7t^4y^7}{6} \)
\( y(1) = \dfrac{1}{2} \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( \dfrac{dy}{dt} + \dfrac{2y}{t} = \dfrac{7t^4y^7}{6} \)
Verilen denklem \( n = 7 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-7} = \dfrac{1}{y^6} \)
\( \dfrac{dz}{dt} = -\dfrac{6}{y^7}\dfrac{dy}{dt} \)
\( \Longrightarrow \dfrac{dy}{dt} = -\dfrac{y^7}{6}\dfrac{dz}{dt} \)
Denklemdeki \( \frac{dy}{dt} \) ifadesi yerine \( \frac{dz}{dt} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( -\dfrac{y^7}{6}\dfrac{dz}{dt} + \dfrac{2y}{t} = \dfrac{7t^4y^7}{6} \)
\( \dfrac{dz}{dt} - \dfrac{12}{ty^6} = -7t^4 \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dt} - \dfrac{12}{t}z = -7t^4 \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(t) = e^{\int {-\frac{12}{t}\ dt}} \)
\( = e^{-12\ln{\abs{t}}} \)
\( = e^{\ln{t^{-12}}} \)
\( = \dfrac{1}{t^{12}} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( \dfrac{1}{t^{12}}\dfrac{dz}{dt} - \dfrac{12}{t^{13}}z = -\dfrac{7}{t^8} \)
Bu eşitliğin sol tarafı, \( \mu(t)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dt}\left( \dfrac{z}{t^{12}} \right) = -\dfrac{7}{t^8} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dt}\left( \dfrac{z}{t^{12}} \right)\ dt} = \displaystyle\int {-\dfrac{7}{t^8}\ dt} \)
\( \dfrac{z}{t^{12}} = \dfrac{1}{t^7} + C \)
\( z = t^5 + Ct^{12} \)
\( z = \frac{1}{y^6} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y^6} = t^5 + Ct^{12} \)
\( y^6 = \dfrac{1}{t^5 + Ct^{12}} \)
\( y(1) = \dfrac{1}{2} \) başlangıç değerini denklemde yerine koyalım.
\( \left( \dfrac{1}{2} \right)^6 = \dfrac{1}{1^5 + C(1)^{12}} \)
\( \dfrac{1}{64} = \dfrac{1}{1 + C} \)
\( C = 63 \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( y^6 = \dfrac{1}{t^5 + 63t^{12}} \)
\( x \gt 0 \) olmak üzere,
\( 2x\dfrac{dy}{dx} + y = 6x^2y^2 \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( \dfrac{dy}{dx} + \dfrac{y}{2x} = 3xy^2 \)
Verilen denklem \( n = 2 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-2} = \dfrac{1}{y} \)
\( \dfrac{dz}{dx} = -\dfrac{1}{y^2}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = -y^2\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( -y^2\dfrac{dz}{dx} + \dfrac{y}{2x} = 3xy^2 \)
\( \dfrac{dz}{dx} - \dfrac{1}{2xy} = -3x \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dx} - \dfrac{1}{2x}z = -3x \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {-\frac{1}{2x}\ dx}} \)
\( = e^{-\frac{1}{2}\ln{\abs{x}}} \)
\( = e^{\ln{x^{-\frac{1}{2}}}} \)
\( = \dfrac{1}{\sqrt{x}} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( \dfrac{1}{\sqrt{x}}\dfrac{dz}{dx} - \dfrac{1}{2x\sqrt{x}}z = -\dfrac{3x}{\sqrt{x}} \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}\left( \dfrac{z}{\sqrt{x}} \right) = -3\sqrt{x} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}\left( \dfrac{z}{\sqrt{x}} \right)\ dx} = \displaystyle\int {-3\sqrt{x}\ dx} \)
\( \dfrac{z}{\sqrt{x}} = -2x\sqrt{x} + C \)
\( z = C\sqrt{x} - 2x^2 \)
\( z = \frac{1}{y} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y} = C\sqrt{x} - 2x^2 \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y = \dfrac{1}{C\sqrt{x} - 2x^2} \)
\( x \gt 0 \) olmak üzere,
\( y' + \dfrac{5y}{x} = x^2y^{\frac{1}{4}} \)
\( y(1) = 9 \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( \dfrac{dy}{dx} + \dfrac{5y}{x} = x^2y^{\frac{1}{4}} \)
Verilen denklem \( n = \frac{1}{4} \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-\frac{1}{4}} = y^{\frac{3}{4}} \)
\( \dfrac{dz}{dx} = \dfrac{3}{4y^{\frac{1}{4}}}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = \dfrac{4y^{\frac{1}{4}}}{3}\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( \dfrac{4y^{\frac{1}{4}}}{3}\dfrac{dz}{dx} + \dfrac{5y}{x} = x^2y^{\frac{1}{4}} \)
\( \dfrac{dz}{dx} + \dfrac{15y^{\frac{3}{4}}}{4x} = \dfrac{3x^2}{4} \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dx} + \dfrac{15}{4x}z = \dfrac{3x^2}{4} \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {\frac{15}{4x}\ dx}} \)
\( = e^{\frac{15}{4}\ln{\abs{x}}} \)
\( = e^{\ln{x^{\frac{15}{4}}}} \)
\( = x^{\frac{15}{4}} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( x^{\frac{15}{4}}\dfrac{dz}{dx} + \dfrac{15x^{\frac{11}{4}}}{4}z = \dfrac{3x^{\frac{23}{4}}}{4} \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}(x^{\frac{15}{4}}z) = \dfrac{3x^{\frac{23}{4}}}{4} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}(x^{\frac{15}{4}}z)\ dx} = \displaystyle\int {\dfrac{3x^{\frac{23}{4}}}{4}\ dx} \)
\( x^{\frac{15}{4}}z = \dfrac{x^{\frac{27}{4}}}{9} + C \)
\( z = \dfrac{x^3}{9} + Cx^{-\frac{15}{4}} \)
\( z = y^{\frac{3}{4}} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( y^{\frac{3}{4}} = \dfrac{x^3}{9} + Cx^{-\frac{15}{4}} \)
\( y(1) = 9 \) başlangıç değerini denklemde yerine koyalım.
\( 9^{\frac{3}{4}} = \dfrac{1^3}{9} + C(1)^{-\frac{15}{4}} \)
\( 3\sqrt{3} = \dfrac{1}{9} + C \)
\( C = 3\sqrt{3} - \dfrac{1}{9} \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( y^{\frac{3}{4}} = \dfrac{x^3}{9} + \left( 3\sqrt{3} - \dfrac{1}{9} \right)x^{-\frac{15}{4}} \)
\( x \gt 0 \) olmak üzere,
\( \dfrac{dy}{dx} + \dfrac{3x^2y}{1 + x^3} = 6x^2y^3 \)
\( y(1) = \dfrac{1}{4} \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterVerilen denklem \( n = 3 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( u \) değişkeni tanımlayalım.
\( u = y^{1-3} = \dfrac{1}{y^2} \)
\( \dfrac{du}{dx} = -\dfrac{2}{y^3}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = -\dfrac{y^3}{2}\dfrac{du}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{du}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( -\dfrac{y^3}{2}\dfrac{du}{dx} + \dfrac{3x^2y}{1 + x^3} = 6x^2y^3 \)
\( \dfrac{du}{dx} - \dfrac{6x^2}{y^2(1 + x^3)} = -12x^2 \)
Denklemdeki \( y \) ifadesi yerine \( u \) karşılığını yazalım.
\( \dfrac{du}{dx} - \dfrac{6x^2}{1 + x^3}u = -12x^2 \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {-\frac{6x^2}{1 + x^3}\ dx}} \)
\( = e^{-2\ln{\abs{1 + x^3}}} \)
\( = e^{\ln{(1 + x^3)^{-2}}} \)
\( = \dfrac{1}{(1 + x^3)^2} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( \dfrac{1}{(1 + x^3)^2}\dfrac{du}{dx} - \dfrac{6x^2}{(1 + x^3)^3}u = -\dfrac{12x^2}{(1 + x^3)^2} \)
Bu eşitliğin sol tarafı, \( \mu(x)u \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}\left( \dfrac{u}{(1 + x^3)^2} \right) = -\dfrac{12x^2}{(1 + x^3)^2} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}\left( \dfrac{u}{(1 + x^3)^2} \right)\ dx} = \displaystyle\int {-\dfrac{12x^2}{(1 + x^3)^2}\ dx} \)
\( v = 1 + x^3 \) ve \( dv = 3x^2\ dx \) şeklinde değişken değiştirerek ifadenin integralini alabiliriz.
\( \dfrac{u}{(1 + x^3)^2} = \dfrac{4}{1 + x^3} + C \)
\( u = 4(1 + x^3) + C(1 + x^3)^2 \)
\( u = \frac{1}{y^2} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y^2} = 4(1 + x^3) + C(1 + x^3)^2 \)
\( y^2 = \dfrac{1}{4(1 + x^3) + C(1 + x^3)^2} \)
\( y(1) = \dfrac{1}{4} \) başlangıç değerini denklemde yerine koyalım.
\( \left( \dfrac{1}{4} \right)^2 = \dfrac{1}{4(1 + 1^3) + C(1 + 1^3)^2} \)
\( \dfrac{1}{16} = \dfrac{1}{4(2) + C(2)^2} \)
\( C = 2 \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( y^2 = \dfrac{1}{4(1 + x^3) + 2(1 + x^3)^2} \)
\( y^2 = \dfrac{1}{(1 + x^3)(6 + 2x^3)} \)
\( t \gt 0 \) olmak üzere,
\( tx' = 3(x - \sqrt{t^3x}) \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( t\dfrac{dx}{dt} = 3x - 3\sqrt{t^3}\sqrt{x} \)
\( \dfrac{dx}{dt} - \dfrac{3x}{t} = -3\sqrt{t}\sqrt{x} \)
Verilen denklem \( n = \frac{1}{2} \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = x^{1-\frac{1}{2}} = \sqrt{x} \)
\( \dfrac{dz}{dt} = \dfrac{1}{2\sqrt{x}}\dfrac{dx}{dt} \)
\( \Longrightarrow \dfrac{dx}{dt} = 2\sqrt{x}\dfrac{dz}{dt} \)
Denklemdeki \( \frac{dx}{dt} \) ifadesi yerine \( \frac{dz}{dt} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( 2\sqrt{x}\dfrac{dz}{dt} - \dfrac{3x}{t} = -3\sqrt{t}\sqrt{x} \)
\( \dfrac{dz}{dt} - \dfrac{3\sqrt{x}}{2t} = -\dfrac{3\sqrt{t}}{2} \)
Denklemdeki \( x \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dt} - \dfrac{3}{2t}z = -\dfrac{3\sqrt{t}}{2} \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(t) = e^{\int {-\frac{3}{2t}\ dt}} \)
\( = e^{-\frac{3}{2}\ln{\abs{t}}} \)
\( = e^{\ln{t^{-\frac{3}{2}}}} \)
\( = \dfrac{1}{t\sqrt{t}} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( \dfrac{1}{t\sqrt{t}}\dfrac{dz}{dt} - \dfrac{3}{2t^2\sqrt{t}}z = -\dfrac{3}{2t} \)
Bu eşitliğin sol tarafı, \( \mu(t)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dt}\left( \dfrac{z}{t\sqrt{t}} \right) = -\dfrac{3}{2t} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dt}\left( \dfrac{z}{t\sqrt{t}} \right)\ dt} = \displaystyle\int {-\dfrac{3}{2t}\ dt} \)
\( \dfrac{z}{t\sqrt{t}} = -\dfrac{3\ln{\abs{t}}}{2} + C \)
\( z = Ct\sqrt{t} - \dfrac{3t\sqrt{t}\ln{t}}{2} \)
\( z = \sqrt{x} \) eşitliğini kullanarak denklemi \( x \) cinsinden yazalım.
\( \sqrt{x} = Ct\sqrt{t} - \dfrac{3t\sqrt{t}\ln{t}}{2} \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( x = \left( Ct\sqrt{t} - \dfrac{3t\sqrt{t}\ln{t}}{2} \right)^2 \)
\( x \gt 0 \) olmak üzere,
\( \dfrac{dy}{dx} + \dfrac{2y}{x} = x^2y^2\tan{x} \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterVerilen denklem \( n = 2 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-2} = \dfrac{1}{y} \)
\( \dfrac{dz}{dx} = -\dfrac{1}{y^2}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = -y^2\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( -y^2\dfrac{dz}{dx} + \dfrac{2y}{x} = x^2y^2\tan{x} \)
\( \dfrac{dz}{dx} - \dfrac{2}{xy} = -x^2\tan{x} \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dx} - \dfrac{2}{x}z = -x^2\tan{x} \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {-\frac{2}{x}\ dx}} \)
\( = e^{-2\ln{\abs{x}}} \)
\( = e^{\ln{x^{-2}}} \)
\( = \dfrac{1}{x^2} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( \dfrac{1}{x^2}\dfrac{dz}{dx} - \dfrac{2}{x^3}z = -\tan{x} \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}\left( \dfrac{z}{x^2} \right) = -\tan{x} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}\left( \dfrac{z}{x^2} \right)\ dx} = \displaystyle\int {-\tan{x}\ dx} \)
\( \dfrac{z}{x^2} = \ln{\abs{\cos{x}}} + C \)
\( z = x^2\ln{\abs{\cos{x}}} + Cx^2 \)
\( z = \dfrac{1}{y} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y} = x^2\ln{\abs{\cos{x}}} + Cx^2 \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y = \dfrac{1}{x^2\ln{\abs{\cos{x}}} + Cx^2} \)
\( y' = y(5 + xy^5) \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( \dfrac{dy}{dx} = 5y + xy^6 \)
\( \dfrac{dy}{dx} - 5y = xy^6 \)
Verilen denklem \( n = 6 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-6} = \dfrac{1}{y^5} \)
\( \dfrac{dz}{dx} = -\dfrac{5}{y^6}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = -\dfrac{y^6}{5}\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( -\dfrac{y^6}{5}\dfrac{dz}{dx} - 5y = xy^6 \)
\( \dfrac{dz}{dx} + \dfrac{25}{y^5} = -5x \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dx} + 25z = -5x \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {25\ dx}} \)
\( = e^{25x} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( e^{25x}\dfrac{dz}{dx} + 25e^{25x}z = -5xe^{25x} \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}(e^{25x}z) = -5xe^{25x} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}(e^{25x}z)\ dx} = \displaystyle\int {-5xe^{25x}\ dx} \)
\( e^{25x}z + C_1 = \displaystyle\int {-5xe^{25x}\ dx} \)
Eşitliğin sağ tarafındaki ifadenin integralini almak için kısmi integral alma yöntemini kullanalım.
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = -5x \)
\( dv = e^{25x}\ dx \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = -5\ dx \)
\( v = \dfrac{e^{25x}}{25} \)
Bu ifadeleri \( \int {u\ dv} = uv - \int {v\ du} \) kısmi integral formülünde yerine koyalım.
\( e^{25x}z + C_1 = -\dfrac{5xe^{25x}}{25} - \displaystyle\int {-\dfrac{5e^{25x}}{25}\ dx} \)
\( e^{25x}z = -\dfrac{xe^{25x}}{5} + \dfrac{e^{25x}}{125} + C_2 \)
\( e^{25x}z = C_2 - \dfrac{xe^{25x}}{5} + \dfrac{e^{25x}}{125} \)
\( z = C_2e^{-25x} - \dfrac{x}{5} + \dfrac{1}{125} \)
\( z = \frac{1}{y^5} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y^5} = C_2e^{-25x} - \dfrac{x}{5} + \dfrac{1}{125} \)
\( y^5 = \dfrac{1}{C_2e^{-25x} - \frac{x}{5} + \frac{1}{125}} \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y^5 = \dfrac{125}{Ce^{-25x} - 25x + 1} \)
\( \dfrac{dy}{dx} + 3y = 8x\sqrt{y} \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterVerilen denklem \( n = \frac{1}{2} \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1 - \frac{1}{2}} = \sqrt{y} \)
\( \dfrac{dz}{dx} = \dfrac{1}{2\sqrt{y}}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = 2\sqrt{y}\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( 2\sqrt{y}\dfrac{dz}{dx} + 3y = 8x\sqrt{y} \)
\( \dfrac{dz}{dx} + \dfrac{3\sqrt{y}}{2} = 4x \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dx} + \dfrac{3}{2}z = 4x \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {\frac{3}{2}\ dx}} \)
\( = e^{\frac{3x}{2}} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( e^{\frac{3x}{2}}\dfrac{dz}{dx} - \dfrac{3e^{\frac{3x}{2}}}{2}z = 4xe^{\frac{3x}{2}} \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}(e^{\frac{3x}{2}}z) = 4xe^{\frac{3x}{2}} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}(e^{\frac{3x}{2}}z)\ dx} = \displaystyle\int {4xe^{\frac{3x}{2}}\ dx} \)
\( e^{\frac{3x}{2}}z + C_1 = \displaystyle\int {4xe^{\frac{3x}{2}}\ dx} \)
Eşitliğin sağ tarafındaki ifadenin integralini almak için kısmi integral alma yöntemini kullanalım.
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = 4x \)
\( dv = e^{\frac{3x}{2}}\ dx \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = 4\ dx \)
\( v = \dfrac{2e^{\frac{3x}{2}}}{3} \)
Bu ifadeleri \( \int {u\ dv} = uv - \int {v\ du} \) kısmi integral formülünde yerine koyalım.
\( e^{\frac{3x}{2}}z + C_1 = \dfrac{8xe^{\frac{3x}{2}}}{3} - \displaystyle\int {\dfrac{8e^{\frac{3x}{2}}}{3}\ dx} \)
\( e^{\frac{3x}{2}}z = \dfrac{8xe^{\frac{3x}{2}}}{3} - \dfrac{16e^{\frac{3x}{2}}}{9} + C \)
\( z = \dfrac{8x}{3} - \dfrac{16}{9} + Ce^{-\frac{3x}{2}} \)
\( z = \sqrt{y} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \sqrt{y} = \dfrac{8x}{3} - \dfrac{16}{9} + Ce^{-\frac{3x}{2}} \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y = \left( \dfrac{8x}{3} - \dfrac{16}{9} + Ce^{-\frac{3x}{2}} \right)^2 \)
\( x \in (0, \frac{\pi}{2}) \) olmak üzere,
\( \sin{x}\dfrac{dy}{dx} + y\cos{x} = 2y^3\sin{x} \)
\( y\left( \dfrac{\pi}{4} \right) = \dfrac{1}{2} \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( \dfrac{dy}{dx} + y\cot{x} = 2y^3 \)
Verilen denklem \( n = 3 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-3} = \dfrac{1}{y^2} \)
\( \dfrac{dz}{dx} = -\dfrac{2}{y^3}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = -\dfrac{y^3}{2}\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( -\dfrac{y^3}{2}\dfrac{dz}{dx} + y\cot{x} = 2y^3 \)
\( \dfrac{dz}{dx} - \dfrac{2\cot{x}}{y^2} = -4 \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dx} - 2z\cot{x} = -4 \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {-2\cot{x}\ dx}} \)
\( = e^{-2\ln{\abs{\sin{x}}}} \)
\( = e^{\ln{(\sin{x})^{-2}}} \)
\( = \csc^2{x} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( \csc^2{x}\dfrac{dz}{dx} - 2z\cot{x}\csc^2{x} = -4\csc^2{x} \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}(z\csc^2{x}) = -4\csc^2{x} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}(z\csc^2{x})} = \displaystyle\int {-4\csc^2{x}\ dx} \)
\( z\csc^2{x} = 4\cot{x} + C \)
\( z = 4\cos{x}\sin{x} + C\sin^2{x} \)
\( z = 2\sin(2x) + C\sin^2{x} \)
\( z = \dfrac{1}{y^2} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y^2} = 2\sin(2x) + C\sin^2{x} \)
\( y^2 = \dfrac{1}{2\sin(2x) + C\sin^2{x}} \)
\( y(\frac{\pi}{4}) = \frac{1}{2} \) başlangıç değerini denklemde yerine koyalım.
\( \left( \dfrac{1}{2} \right)^2 = \dfrac{1}{2\sin(2 \cdot \frac{\pi}{4}) + C\sin^2{\frac{\pi}{4}}} \)
\( \dfrac{1}{4} = \dfrac{1}{2 + \frac{C}{2}} \)
\( C = 4 \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( y^2 = \dfrac{1}{2\sin(2x) + 4\sin^2{x}} \)
\( x \gt 0 \) olmak üzere,
\( 3xy' = 3x^2y^2\ln{x} - y \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( 3x\dfrac{dy}{dx} + y = 3x^2y^2\ln{x} \)
\( \dfrac{dy}{dx} + \dfrac{y}{3x} = xy^2\ln{x} \)
Verilen denklem \( n = 2 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-2} = \dfrac{1}{y} \)
\( \dfrac{dz}{dx} = -\dfrac{1}{y^2}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = -y^2\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( -y^2\dfrac{dz}{dx} + \dfrac{y}{3x} = xy^2\ln{x} \)
\( \dfrac{dz}{dx} - \dfrac{1}{3xy} = -x\ln{x} \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dx} - \dfrac{1}{3x}z = -x\ln{x} \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {-\frac{1}{3x}\ dx}} \)
\( = e^{-\frac{1}{3}\ln{\abs{x}}} \)
\( = e^{\ln{x^{-\frac{1}{3}}}} \)
\( = \dfrac{1}{\sqrt[3]{x}} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( \dfrac{1}{\sqrt[3]{x}}\dfrac{dz}{dx} - \dfrac{z}{3x\sqrt[3]{x}} = -\sqrt[3]{x^2}\ln{x} \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}\left( \dfrac{z}{\sqrt[3]{x}} \right) = -\sqrt[3]{x^2}\ln{x} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}\left( \dfrac{z}{\sqrt[3]{x}} \right)\ dx} = \displaystyle\int {-\sqrt[3]{x^2}\ln{x}\ dx} \)
\( \dfrac{z}{\sqrt[3]{x}} + C_1 = \displaystyle\int {-\sqrt[3]{x^2}\ln{x}\ dx} \)
Eşitliğin sağ tarafındaki ifadenin integralini almak için kısmi integral alma yöntemini kullanalım.
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = \ln{x} \)
\( dv = -\sqrt[3]{x^2}\ dx \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = \dfrac{1}{x}\ dx \)
\( v = -\dfrac{3x\sqrt[3]{x^2}}{5} \)
Bu ifadeleri \( \int {u\ dv} = uv - \int {v\ du} \) kısmi integral formülünde yerine koyalım.
\( \dfrac{z}{\sqrt[3]{x}} + C_1 = -\dfrac{3x\sqrt[3]{x^2}\ln{x}}{5} - \displaystyle\int {-\dfrac{3\sqrt[3]{x^2}}{5}\ dx} \)
\( \dfrac{z}{\sqrt[3]{x}} = -\dfrac{3x\sqrt[3]{x^2}\ln{x}}{5} + \dfrac{9x\sqrt[3]{x^2}}{25} + C_2 \)
\( z = C_2\sqrt[3]{x} - \dfrac{3x^2\ln{x}}{5} + \dfrac{9x^2}{25} \)
\( z = \dfrac{1}{y} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y} = C_2\sqrt[3]{x} - \dfrac{3x^2\ln{x}}{5} + \dfrac{9x^2}{25} \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y = \dfrac{25}{C\sqrt[3]{x} - 15x^2\ln{x} + 9x^2} \)
\( x \gt 0 \) olmak üzere,
\( \dfrac{dy}{dx} - \dfrac{y}{2x} = xy^3\cos{x} \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterVerilen denklem \( n = 3 \) olan bir Bernoulli denklemidir.
Aşağıdaki şekilde bir \( z \) değişkeni tanımlayalım.
\( z = y^{1-3} = \dfrac{1}{y^2} \)
\( \dfrac{dz}{dx} = -\dfrac{2}{y^3}\dfrac{dy}{dx} \)
\( \Longrightarrow \dfrac{dy}{dx} = -\dfrac{y^3}{2}\dfrac{dz}{dx} \)
Denklemdeki \( \frac{dy}{dx} \) ifadesi yerine \( \frac{dz}{dx} \) karşılığını yazalım ve denklemi standart forma getirelim.
\( -\dfrac{y^3}{2}\dfrac{dz}{dx} - \dfrac{y}{2x} = xy^3\cos{x} \)
\( \dfrac{dz}{dx} + \dfrac{1}{y^2x} = -2x\cos{x} \)
Denklemdeki \( y \) ifadesi yerine \( z \) karşılığını yazalım.
\( \dfrac{dz}{dx} + \dfrac{1}{x}z = -2x\cos{x} \)
Elde ettiğimiz standart formdaki birinci mertebeden lineer denklemi çözelim.
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {\frac{1}{x}\ dx}} \)
\( = e^{\ln{\abs{x}}} \)
\( = x \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( x\dfrac{dz}{dx} + z = -2x^2\cos{x} \)
Bu eşitliğin sol tarafı, \( \mu(x)z \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}(xz) = -2x^2\cos{x} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {\dfrac{d}{dx}(xz)\ dx} = \displaystyle\int {-2x^2\cos{x}\ dx} \)
\( xz + C_1 = \displaystyle\int {-2x^2\cos{x}\ dx} \)
Eşitliğin sağ tarafındaki ifadenin integralini almak için kısmi integral alma yöntemini kullanalım.
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = -2x^2 \)
\( dv = \cos{x}\ dx \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = -4x\ dx \)
\( v = \sin{x} \)
Bu ifadeleri \( \int {u\ dv} = uv - \int {v\ du} \) kısmi integral formülünde yerine koyalım.
\( xz + C_1 = -2x^2\sin{x} - \displaystyle\int {-4x\sin{x}\ dx} \)
\( xz + C_1 = -2x^2\sin{x} + \displaystyle\int {4x\sin{x}\ dx} \)
Eşitliğin sağ tarafındaki ifadenin integralini almak için tekrar kısmi integral alma yöntemini kullanalım.
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = 4x \)
\( dv = \sin{x}\ dx \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = 4\ dx \)
\( v = -\cos{x} \)
Bu ifadeleri \( \int {u\ dv} = uv - \int {v\ du} \) kısmi integral formülünde yerine koyalım.
\( xz + C_1 = -2x^2\sin{x} + (-4x\cos{x}) - \displaystyle\int {-4\cos{x}\ dx} \)
\( xz = -2x^2\sin{x} - 4x\cos{x} + 4\sin{x} + C \)
\( z = -2x\sin{x} - 4\cos{x} + \dfrac{4\sin{x}}{x} + \dfrac{C}{x} \)
\( z = \frac{1}{y^2} \) eşitliğini kullanarak denklemi \( y \) cinsinden yazalım.
\( \dfrac{1}{y^2} = -2x\sin{x} - 4\cos{x} + \dfrac{4\sin{x}}{x} + \dfrac{C}{x} \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y^2 = \dfrac{x}{4\sin{x} + C - 2x^2\sin{x} - 4x\cos{x}} \)