Tam Denklemler
\( \frac{dy}{dx} = f(x, y) \) formundaki birinci mertebeden bir diferansiyel denklem aşağıdaki iki formda yazılabilir.
\( M(x, y) + N(x, y)\dfrac{dy}{dx} = 0 \)
\( M(x, y)\ dx + N(x, y)\ dy = 0 \)
\( \dfrac{dy}{dx} = \dfrac{y - 2x^3y^2}{x^4y - x} \)
\( (x^4y - x)\dfrac{dy}{dx} = y - 2x^3y^2 \)
Tüm terimler sol tarafta toplandığında birinci form elde edilir.
\( \underbrace{(2x^3y^2 - y)}_{M(x, y)} + \underbrace{(x^4y - x)}_{N(x, y)}\dfrac{dy}{dx} = 0 \)
Bu eşitlik alternatif olarak aşağıdaki diferansiyel formunda da yazılabilir.
\( \underbrace{(2x^3y^2 - y)}_{M(x, y)}\ dx + \underbrace{(x^4y - x)}_{N(x, y)}\ dy = 0 \)
Bu denklemdeki \( M \) ve \( N \) fonksiyonlarının iki değişkenli bir \( F(x, y) \) fonksiyonunun sırasıyla \( x \) ve \( y \) değişkenlerine göre kısmi türevleri olduğunu varsayalım.
\( \dfrac{\partial F(x, y)}{\partial x} = F_x(x, y) = M(x, y) \)
\( \dfrac{\partial F(x, y)}{\partial y} = F_y(x, y) = N(x, y) \)
Bu durumda verilen denklem \( F \) fonksiyonunun toplam diferansiyeli şeklinde aşağıdaki gibi yazılabilir.
\( M(x, y)\ dx + N(x, y)\ dy = 0 \)
\( F_x(x, y)\ dx + F_y(x, y)\ dy = 0 \)
\( \dfrac{dF(x, y)}{dx} = 0 \)
Her iki tarafın \( x \) değişkenine göre integralini alalım.
\( \displaystyle\int {\dfrac{dF(x, y)}{dx}\ dx} = \displaystyle\int {0\ dx} \)
\( F(x, y) = C \)
Buna göre, \( M(x, y)\ dx + N(x, y)\ dy = 0 \) formundaki bir diferansiyel denklem belirli bir \( F(x, y) \) fonksiyonu için \( F_x = M \) ve \( F_y = N \) eşitliklerini sağlıyorsa aşağıdaki iki sonuca varabiliriz.
- Eşitliğin sol tarafı \( F(x, y) \) şeklindeki bir fonksiyonun toplam diferansiyelidir.
- Denklemin genel çözümü \( F(x, y) = C \) olur.
Bu doğrultuda tam diferansiyel denklemler aşağıdaki şekilde tanımlanabilir.
\( M(x, y)\ dx + N(x, y)\ dy = 0 \) denklemi,
bir \( F(x, y) \) fonksiyonu için aşağıdaki iki eşitlik sağlanıyorsa bir tam diferansiyel denklemdir.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
Tam diferansiyel denklemler lineer olabilir ya da olmayabilir.
İki değişkenli fonksiyonlarda geçerli olan \( F_{xy}(x, y) = F_{yx}(x, y) \) eşitliğini kullanırsak, bu formdaki bir denklem tam diferansiyel denklem ise \( M(x, y) \) fonksiyonunun \( y \) değişkenine göre kısmi türevi, \( N(x, y) \) fonksiyonunun \( x \) değişkenine göre kısmi türevine eşit olmalıdır. Buna göre, bir diferansiyel denklemin tam olup olmadığı aşağıdaki testle bulunabilir.
\( M(x, y), N(x, y), M_y(x, y), N_x(x, y) \) fonksiyonları dikdörtgensel bir \( R \) bölgesinde sürekli fonksiyonlar olmak üzere,
\( M_y(x, y) = N_x(x, y) \)
eşitliği sağlanıyorsa verilen denklem bir tam diferansiyel denklemdir.
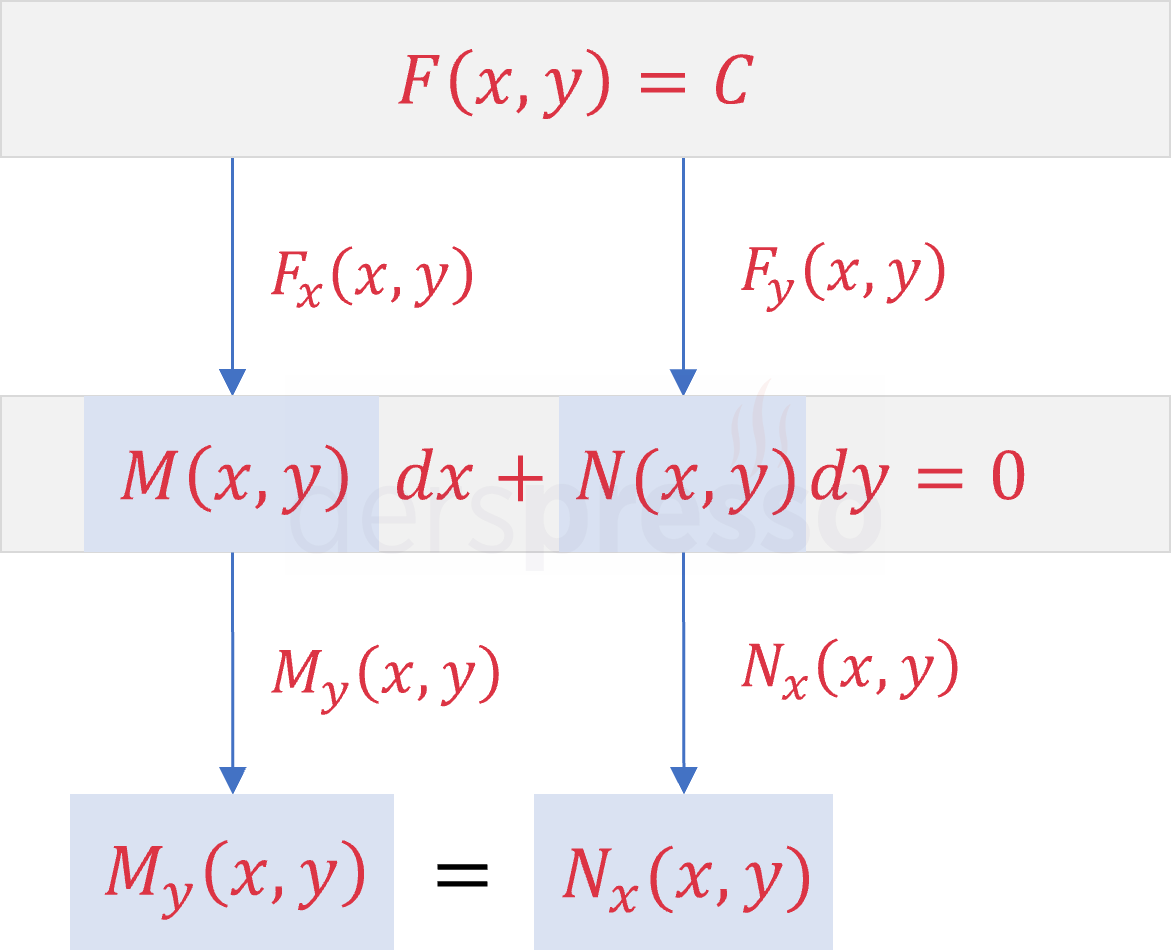
Bu testte \( dx \) katsayısı olan \( M \) fonksiyonunun \( y \) değişkenine göre kısmi türevi ile \( dy \) katsayısı olan \( N \) fonksiyonunun \( x \) değişkenine göre kısmi türevinin karşılaştırıldığına dikkat edilmelidir.
Tam denklem testini bir örnek üzerinde gösterelim.
\( (3x^2 + 2xy^3)\ dx + (3x^2y^2 + 4y^3)\ dy = 0 \)
denkleminin tam diferansiyel denklem olup olmadığını bulalım.
\( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = 3x^2 + 2xy^3 \)
\( N(x, y) = 3x^2y^2 + 4y^3 \)
Denklemin tam olması için \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = 6xy^2 \)
\( N_x(x, y) = 6xy^2 \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Tam denklemler aşağıdaki yöntemle çözülür.
Adım 1: Denklemin formu
Verilen denklem önce aşağıdaki forma getirilir, \( M \) ve \( N \) fonksiyonları belirlenir.
\( M(x, y)\ dx + N(x, y)\ dy = 0 \)
Adım 2: Tam denklem testi
Denklemin tam denklem koşulunu sağlayıp sağlamadığı kontrol edilir. \( M \) fonksiyonunun \( y \) değişkenine göre kısmi türevi \( N \) fonksiyonunun \( x \) değişkenine göre kısmi türevine eşitse denklem bir tam denklemdir.
\( M_y(x, y) = N_x(x, y) \)
Adım 3: \( F \) fonksiyonunun bulunması
Denklem bir tam denklem ise \( M \) fonksiyonunun \( x \) değişkenine göre integrali alınır.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} + g(y) \)
\( M \) fonksiyonu \( F \) fonksiyonunun \( x \) değişkenine göre kısmi türevi olduğu ve bu türev işleminde sadece \( y \) değişkenine bağlı olan terimler kaybolacağı için, integral işleminin sonucuna integral sabiti olarak \( g(y) \) şeklinde sadece \( y \) değişkenine bağlı bir fonksiyon eklenir.
Alternatif yöntem: İntegral işlemlerinin kolaylığına göre, bu adımda \( N \) fonksiyonunun \( y \) değişkenine göre integrali alınarak da \( F \) fonksiyonu bulunabilir. Bu durumda integral işleminin sonucuna integral sabiti olarak \( h(x) \) şeklinde sadece \( x \) değişkenine bağlı bir fonksiyon eklenir.
\( F(x, y) = \displaystyle\int {N(x, y)\ dy} + h(x) \)
Adım 4: \( F \) fonksiyonunun türevi
Bulunan \( F \) fonksiyonunun \( y \) değişkenine göre türevi alınarak \( N(x, y) \) fonksiyonuna eşitlenir ve \( g'(y) \) fonksiyonu bulunur.
\( F_y(x, y) = N(x, y) \)
Alternatif yöntem: Bu durumda \( F \) fonksiyonunun \( x \) değişkenine göre türevi alınarak \( M(x, y) \) fonksiyonuna eşitlenir ve \( h'(x) \) fonksiyonu bulunur.
\( F_x(x, y) = M(x, y) \)
Adım 5: \( g(y) \) fonksiyonunun bulunması
\( g'(y) \) fonksiyonunun \( y \) değişkenine göre integrali alınarak \( g(y) \) fonksiyonu bulunur.
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Alternatif yöntem: \( h'(x) \) fonksiyonunun \( x \) değişkenine göre integrali alınarak \( h(x) \) fonksiyonu bulunur.
Adım 6: Genel çözümün bulunması
Elde edilen \( F(x, y) = C \) şeklindeki denklem diferansiyel denklemin genel çözümüdür.
Adım 7: Başlangıç koşulları
Denklem için başlangıç koşulları verildiyse genel çözümde yerine konarak keyfi sabitler ve denklemin özel çözümü bulunur.
Tam denklemlerin çözümünü bir örnek üzerinde gösterelim.
\( (y^2\cos{x} - 2\sin{x})\ dx + (2y\sin{x} + 3)\ dy = 0 \)
denkleminin genel çözümünü bulalım.
Önce verilen denklem için \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = y^2\cos{x} - 2\sin{x} \)
\( N(x, y) = 2y\sin{x} + 3 \)
Denklemin tam olması için \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = 2y\cos{x} \)
\( N_x(x, y) = 2y\cos{x} \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( M(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} \)
\( = \displaystyle\int {(y^2\cos{x} - 2\sin{x})\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = y^2\sin{x} + 2\cos{x} + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, y) \) fonksiyonuna eşitleyelim.
\( F_y(x, y) = N(x, y) \)
\( 2y\sin{x} + g'(y) = 2y\sin{x} + 3 \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = 3 \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {3\ dy} \)
\( g(y) = 3y \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( y^2\sin{x} + 2\cos{x} + 3y = C \)
Aşağıdaki denklemlerin tam diferansiyel denklem olup olmadığını bulunuz.
(a) \( (3x^2y^2 + 7x)\ dx + (2x^3y + 10y^3)\ dy = 0 \)
(b) \( (y\sin{t} + y^3\cos{t})\ dt + (\cos{t} + y^2\sin{t})\ dy = 0 \)
(c) \( (\tan{x} + xye^x)\ dx + (y\sin(2y) + xe^x - e^x)\ dy = 0 \)
Çözümü Göster(a) seçeneği:
\( (3x^2y^2 + 7x)\ dx + (2x^3y + 10y^3)\ dy = 0 \)
\( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = 3x^2y^2 + 7x \)
\( N(x, y) = 2x^3y + 10y^3 \)
Bir denklemin tam olması için \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = 6x^2y \)
\( N_x(x, y) = 6x^2y \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
(b) seçeneği:
\( (y\sin{t} + y^3\cos{t})\ dt + (\cos{t} + y^2\sin{t})\ dy = 0 \)
\( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(t, y) = y\sin{t} + y^3\cos{t} \)
\( N(t, y) = \cos{t} + y^2\sin{t} \)
Bir denklemin tam olması için \( M_y(t, y) = N_t(t, y) \) eşitliği sağlanmalıdır.
\( M_y(t, y) = \sin{t} + 3y^2\cos{t} \)
\( N_t(t, y) = -\sin{t} + y^2\cos{t} \)
\( M_y(t, y) \ne N_t(t, y) \) olduğu için verilen denklem bir tam diferansiyel denklem değildir.
(c) seçeneği:
\( (\tan{x} + xye^x)\ dx + (y\sin(2y) + xe^x - e^x)\ dy = 0 \)
\( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = \tan{x} + xye^x \)
\( N(x, y) = y\sin(2y) + xe^x - e^x \)
Bir denklemin tam olması için \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = xe^x \)
\( N_x(x, y) = e^x + xe^x - e^x \)
\( = xe^x \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
\( M(x, y)\ dx + (x^2y^2 + \ln(xy))\ dy = 0 \)
bir tam diferansiyel denklem olduğuna göre, \( M(x, y) \) fonksiyonunun \( y \) değişkenine bağlı terimlerini bulunuz.
Çözümü Göster\( N \) fonksiyonunu belirleyelim.
\( N(x, y) = x^2y^2 + \ln(xy) \)
Denklem tam olduğuna göre fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( N_x(x, y) = 2xy^2 + \dfrac{1}{x} \)
\( M_y(x, y) = N_x(x, y) = 2xy^2 + \dfrac{1}{x} \)
\( M_y(x, y) \) fonksiyonunun \( y \) değişkenine göre integralini alarak \( M(x, y) \) fonksiyonunu bulalım.
\( M(x, y) = \displaystyle\int {M_y(x, y)\ dy} \)
\( = \displaystyle\int {\left( 2xy^2 + \dfrac{1}{x} \right)\ dy} \)
\( y \) değişkenine göre alınan integralin \( x \) değişkenine bağlı integral sabitine \( h(x) \) diyelim.
\( = \dfrac{2xy^3}{3} + \dfrac{y}{x} + h(x) \)
Buna göre denklemi tam yapan \( M(x, y) \) fonksiyonunun genel formu aşağıdaki gibidir.
\( M(x, y) = \dfrac{2xy^3}{3} + \dfrac{y}{x} + h(x) \)
\( M(x, y) \) fonksiyonunun \( y \) değişkenine bağlı terimleri aşağıdaki gibi bulunur.
\( \dfrac{2xy^3}{3} + \dfrac{y}{x} \)
\( (e^{y^2} + y^3\cos{x} + 5x^3)\ dx + N(x, y)\ dy = 0 \)
bir tam diferansiyel denklem olduğuna göre, \( N(x, y) \) fonksiyonunun \( x \) değişkenine bağlı terimlerini bulunuz.
Çözümü Göster\( M \) fonksiyonunu belirleyelim.
\( M(x, y) = e^{y^2} + y^3\cos{x} + 5x^3 \)
Denklem tam olduğuna göre fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = 2ye^{y^2} + 3y^2\cos{x} \)
\( N_x(x, y) = M_y(x, y) = 2ye^{y^2} + 3y^2\cos{x} \)
\( N_x(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( N(x, y) \) fonksiyonunu bulalım.
\( N(x, y) = \displaystyle\int {N_x(x, y)\ dx} \)
\( = \displaystyle\int {(2ye^{y^2} + 3y^2\cos{x})\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = 2xye^{y^2} + 3y^2\sin{x} + g(y) \)
Buna göre denklemi tam yapan \( N(x, y) \) fonksiyonunun genel formu aşağıdaki gibidir.
\( N(x, y) = 2xye^{y^2} + 3y^2\sin{x} + g(y) \)
\( N(x, y) \) fonksiyonunun \( x \) değişkenine bağlı terimleri aşağıdaki gibi bulunur.
\( 2xye^{y^2} + 3y^2\sin{x} \)
\( (2x + 5y)\ dx + (5x - y^2)\ dy = 0 \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = 2x + 5y \)
\( N(x, y) = 5x - y^2 \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = 5 \)
\( N_x(x, y) = 5 \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( M(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} \)
\( = \displaystyle\int {(2x + 5y)\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = x^2 + 5xy + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, y) \) fonksiyonuna eşitleyelim.
\( F_y(x, y) = N(x, y) \)
\( 5x + g'(y) = 5x - y^2 \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = -y^2 \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {-y^2\ dy} \)
\( g(y) = -\dfrac{y^3}{3} \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( x^2 + 5xy - \dfrac{y^3}{3} = C \)
\( (x^4 + 6x^2y - 3y^2)\ dx + (2x^3 - 6xy + y^3)\ dy = 0 \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = x^4 + 6x^2y - 3y^2 \)
\( N(x, y) = 2x^3 - 6xy + y^3 \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = 6x^2 - 6y \)
\( N_x(x, y) = 6x^2 - 6y \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( N(x, y) \) fonksiyonunun \( y \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {N(x, y)\ dy} \)
\( = \displaystyle\int {(2x^3 - 6xy + y^3)\ dy} \)
\( y \) değişkenine göre alınan integralin \( x \) değişkenine bağlı integral sabitine \( h(x) \) diyelim.
\( = 2x^3y - 3xy^2 + \dfrac{y^4}{4} + h(x) \)
\( h(x) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( x \) değişkenine göre türevini alarak \( M(x, y) \) fonksiyonuna eşitleyelim.
\( F_x(x, y) = M(x, y) \)
\( 6x^2y - 3y^2 + h'(x) = x^4 + 6x^2y - 3y^2 \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( h'(x) \) aşağıdaki gibi bulunur.
\( h'(x) = x^4 \)
Tarafların \( x \) değişkenine göre integralini alalım.
\( \displaystyle\int {h'(x)\ dx} = \displaystyle\int {x^4\ dx} \)
\( h(x) = \dfrac{x^5}{5} \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( \dfrac{x^5}{5} + 2x^3y - 3xy^2 + \dfrac{y^4}{4} = C \)
\( (8x - 4x^2y^3)\ dx + (y^5 - 4x^3y^2)\ dy = 0 \)
\( y(2) = 1 \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterDenklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = 8x - 4x^2y^3 \)
\( N(x, y) = y^5 - 4x^3y^2 \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = -12x^2y^2 \)
\( N_x(x, y) = -12x^2y^2 \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( M(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} \)
\( = \displaystyle\int {(8x - 4x^2y^3)\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = 4x^2 - \dfrac{4}{3}x^3y^3 + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, y) \) fonksiyonuna eşitleyelim.
\( F_y(x, y) = N(x, y) \)
\( -4x^3y^2 + g'(y) = y^5 - 4x^3y^2 \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = y^5 \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {y^5\ dy} \)
\( g(y) = \dfrac{y^6}{6} \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( 4x^2 - \dfrac{4}{3}x^3y^3 + \dfrac{y^6}{6} = C \)
\( y(2) = 1 \) başlangıç değerini denklemde yerine koyalım.
\( 4(2)^2 - \dfrac{4}{3}(2)^3(1)^3 + \dfrac{1^6}{6} = C \)
\( 16 - \dfrac{32}{3} + \dfrac{1}{6} = C \)
\( C = \dfrac{11}{2} \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( 4x^2 - \dfrac{4}{3}x^3y^3 + \dfrac{y^6}{6} = \dfrac{11}{2} \)
\( \cos{x}\sin{y} - \sec^2{x} + (\sin{x}\cos{y} - \tan{y})\dfrac{dy}{dx} = 0 \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( (\cos{x}\sin{y} - \sec^2{x})\ dx + (\sin{x}\cos{y} + \tan{y})\ dy = 0 \)
Denklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = \cos{x}\sin{y} - \sec^2{x} \)
\( N(x, y) = \sin{x}\cos{y} - \tan{y} \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = \cos{x}\cos{y} \)
\( N_x(x, y) = \cos{x}\cos{y} \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( M(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} \)
\( = \displaystyle\int {(\cos{x}\sin{y} - \sec^2{x})\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = \sin{x}\sin{y} - \tan{x} + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, y) \) fonksiyonuna eşitleyelim.
\( F_y(x, y) = N(x, y) \)
\( \sin{x}\cos{y} + g'(y) = \sin{x}\cos{y} - \tan{y} \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = -\tan{y} \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {-\tan{y}\ dy} \)
\( g(y) = \ln{\abs{\cos{y}}} \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( \sin{x}\sin{y} - \tan{x} + \ln{\abs{\cos{y}}} = C \)
\( e^{t^2}(4ty + 2t) + (2e^{t^2} + 1)y' = 0 \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( e^{t^2}(4ty + 2t) + (2e^{t^2} + 1)\dfrac{dy}{dt} = 0 \)
\( e^{t^2}(4ty + 2t)\ dt + (2e^{t^2} + 1)\ dy = 0 \)
Denklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(t, y) = e^{t^2}(4ty + 2t) \)
\( N(t, y) = 2e^{t^2} + 1 \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(t, y) = N_t(t, y) \) eşitliği sağlanmalıdır.
\( M_y(t, y) = 4te^{t^2} \)
\( N_t(t, y) = 4te^{t^2} \)
\( M_y(t, y) = N_t(t, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(t, y) = C \) fonksiyonu vardır.
\( F_t(t, y) = M(t, y) \)
\( F_y(t, y) = N(t, y) \)
\( M(t, y) \) fonksiyonunun \( t \) değişkenine göre integralini alarak \( F(t, y) \) fonksiyonunu bulalım.
\( F(t, y) = \displaystyle\int {M(t, y)\ dt} \)
\( = \displaystyle\int {(e^{t^2}(4ty + 2t))\ dt} \)
\( = \displaystyle\int {(4tye^{t^2} + 2te^{t^2})\ dt} \)
Bu integrali \( u = t^2 \) ve \( du = 2t\ dt \) şeklinde değişken değiştirerek alabiliriz.
\( t \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = 2ye^{t^2} + e^{t^2} + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(t, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(t, y) \) fonksiyonuna eşitleyelim.
\( F_y(t, y) = N(t, y) \)
\( 2e^{t^2} + g'(y) = 2e^{t^2} + 1 \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = 1 \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {1\ dy} \)
\( g(y) = y \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(t, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( 2ye^{t^2} + e^{t^2} + y = C \)
\( (y\sec^2{x} + y^2e^x)\ dx + (\tan{x} + 2ye^x + 6y^2)\ dy = 0 \)
\( y(0) = 3 \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterDenklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = y\sec^2{x} + y^2e^x \)
\( N(x, y) = \tan{x} + 2ye^x + 6y^2 \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = \sec^2{x} + 2ye^x \)
\( N_x(x, y) = \sec^2{x} + 2ye^x \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( M(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} \)
\( = \displaystyle\int {(y\sec^2{x} + y^2e^x)\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = y\tan{x} + y^2e^x + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, y) \) fonksiyonuna eşitleyelim.
\( F_y(x, y) = N(x, y) \)
\( \tan{x} + 2ye^x + g'(y) = \tan{x} + 2ye^x + 6y^2 \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = 6y^2 \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {6y^2\ dy} \)
\( g(y) = 2y^3 \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( y\tan{x} + y^2e^x + 2y^3 = C \)
\( y(0) = 3 \) başlangıç değerini denklemde yerine koyalım.
\( 3\tan{0} + 3^2e^0 + 2(3)^3 = C \)
\( 0 + 9 + 54 = C \)
\( C = 63 \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( y\tan{x} + y^2e^x + 2y^3 = 63 \)
\( (2x\sin{y} - e^x\ln(\cos{y}) + y^3)\ dx + (x^2\cos{y} + e^x\tan{y} + 3xy^2 + e^y)\ dy = 0 \)
\( y(0) = 0 \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterDenklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = 2x\sin{y} - e^x\ln(\cos{y}) + y^3 \)
\( N(x, y) = x^2\cos{y} + e^x\tan{y} + 3xy^2 + e^y \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = 2x\cos{y} + e^x\tan{y} + 3y^2 \)
\( N_x(x, y) = 2x\cos{y} + e^x\tan{y} + 3y^2 \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( M(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} \)
\( = \displaystyle\int {(2x\sin{y} - e^x\ln(\cos{y}) + y^3)\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = x^2\sin{y} - e^x\ln(\cos{y}) + xy^3 + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, y) \) fonksiyonuna eşitleyelim.
\( F_y(x, y) = N(x, y) \)
\( x^2\cos{y} + e^x\tan{y} + 3xy^2 + g'(y) = x^2\cos{y} + e^x\tan{y} + 3xy^2 + e^y \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = e^y \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {e^y\ dy} \)
\( g(y) = e^y \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( x^2\sin{y} - e^x\ln(\cos{y}) + xy^3 + e^y = C \)
\( y(0) = 0 \) başlangıç değerini denklemde yerine koyalım.
\( 0^2\sin{0} - e^0\ln(\cos{0}) + 0(0)^3 + e^0 = C \)
\( 0 - 0 + 0 + 1 = C \)
\( C = 1 \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( x^2\sin{y} - e^x\ln(\cos{y}) + xy^3 + e^y = 1 \)
\( 4x^3e^y - 3x^2\cot{y} + (x^4e^y + x^3\csc^2{x})\dfrac{dy}{dx} = 0 \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( (4x^3e^y - 3x^2\cot{y})\ dx + (x^4e^y + x^3\csc^2{x})\ dy = 0 \)
Denklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = 4x^3e^y - 3x^2\cot{y} \)
\( N(x, y) = x^4e^y + x^3\csc^2{y} \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = 4x^3e^y + 3x^2\csc^2{x} \)
\( N_x(x, y) = 4x^3e^y + 3x^2\csc^2{x} \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( M(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} \)
\( = \displaystyle\int {(4x^3e^y - 3x^2\cot{y})\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = x^4e^y - x^3\cot{y} + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, y) \) fonksiyonuna eşitleyelim.
\( F_y(x, y) = N(x, y) \)
\( x^4e^y + x^3\csc^2{x} + g'(y) = x^4e^y + x^3\csc^2{y} \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = 0 \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {0\ dy} \)
\( g(y) = 0 \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
\( x^4e^y - x^3\cot{y} + 0 = C \)
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( x^4e^y - x^3\cot{y} = C \)
\( (t\csc{x} + 3t)\ dt - \left( \dfrac{t^2}{2}\cot{x}\csc{x} + x \right)\ dx = 0 \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(t, x) = t\csc{x} + 3t \)
\( N(t, x) = -\dfrac{t^2}{2}\cot{x}\csc{x} - x \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(t, y) = N_t(t, y) \) eşitliği sağlanmalıdır.
\( M_x(t, x) = -t\cot{x}\csc{x} \)
\( N_t(t, x) = -t\cot{x}\csc{x} \)
\( M_x(t, x) = N_t(t, x) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(t, x) = C \) fonksiyonu vardır.
\( F_t(t, x) = M(t, x) \)
\( F_x(t, x) = N(t, x) \)
\( N(t, x) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(t, x) \) fonksiyonunu bulalım.
\( F(t, x) = \displaystyle\int {N(t, x)\ dx} \)
\( = \displaystyle\int {\left( -\dfrac{t^2}{2}\cot{x}\csc{x} - x \right)\ dx} \)
\( x \) değişkenine göre alınan integralin \( t \) değişkenine bağlı integral sabitine \( h(t) \) diyelim.
\( = \dfrac{t^2}{2}\csc{x} - \dfrac{x^2}{2} + h(t) \)
\( h(t) \) fonksiyonunu bulmak için \( F(t, x) \) fonksiyonunun \( t \) değişkenine göre türevini alarak \( M(t, x) \) fonksiyonuna eşitleyelim.
\( F_t(t, x) = M(t, x) \)
\( t\csc{x} + h'(t) = t\csc{x} + 3t \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( h'(t) \) aşağıdaki gibi bulunur.
\( h'(t) = 3t \)
Tarafların \( t \) değişkenine göre integralini alalım.
\( \displaystyle\int {h'(t)\ dt} = \displaystyle\int {3t\ dt} \)
\( h(t) = \dfrac{3t^2}{2} \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(t, x) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( \dfrac{t^2}{2}\csc{x} - \dfrac{x^2}{2} + \dfrac{3t^2}{2} = C \)
\( (ye^{xy} - xe^y + 3x^2)\ dx + \left( xe^{xy} - \dfrac{x^2e^{y}}{2} + ye^y \right)\ dy = 0 \)
\( y(1) = 2 \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterDenklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = ye^{xy} - xe^y + 3x^2 \)
\( N(x, y) = xe^{xy} - \dfrac{x^2e^{y}}{2} + ye^y \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = e^{xy} + xye^{xy} - xe^y \)
\( N_x(x, y) = e^{xy} + xye^{xy} - xe^y \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( M(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} \)
\( = \displaystyle\int {(ye^{xy} - xe^y + 3x^2)\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = e^{xy} - \dfrac{x^2e^y}{2} + x^3 + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, y) \) fonksiyonuna eşitleyelim.
\( F_y(x, y) = N(x, y) \)
\( xe^{xy} - \dfrac{x^2e^y}{2} + g'(y) = xe^{xy} - \dfrac{x^2e^{y}}{2} + ye^y \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = ye^y \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {ye^y\ dy} \)
Eşitliğin sağ tarafındaki ifadenin integralini almak için kısmi integral alma yöntemini kullanalım.
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = y \)
\( dv = e^y\ dy \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = dy \)
\( v = e^y \)
Bu ifadeleri \( \int {u\ dv} = uv - \int {v\ du} \) kısmi integral formülünde yerine koyalım.
\( g(y) = ye^y - \displaystyle\int {e^y\ dy} \)
\( = ye^y - e^y \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( e^{xy} - \dfrac{x^2e^y}{2} + x^3 + ye^y - e^y = C \)
\( y(1) = 2 \) başlangıç değerini denklemde yerine koyalım.
\( e^{(1)(2)} - \dfrac{1^2e^2}{2} + 1^3 + 2e^2 - e^2 = C \)
\( e^2 - \dfrac{e^2}{2} + 1 + 2e^2 - e^2 = C \)
\( C = \dfrac{3e^2}{2} + 1 \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( e^{xy} - \dfrac{x^2e^y}{2} + x^3 + ye^y - e^y = \dfrac{3e^2}{2} + 1 \)
\( -7ty' - \dfrac{ty'}{1 + y^2} = 7y + \arctan{y} + e^{2t} \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( -(7t + \dfrac{t}{1 + y^2})\dfrac{dy}{dt} = 7y + \arctan{y} + e^{2t} \)
\( -(7t + \dfrac{t}{1 + y^2})\ dy = (7y + \arctan{y} + e^{2t})\ dt \)
\( (7y + \arctan{y} + e^{2t})\ dt + (7t + \dfrac{t}{1 + y^2})\ dy = 0 \)
Denklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(t, y) = 7y + \arctan{y} + e^{2t} \)
\( N(t, y) = 7t + \dfrac{t}{1 + y^2} \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(t, y) = N_t(t, y) \) eşitliği sağlanmalıdır.
\( M_y(t, y) = 7 + \dfrac{1}{1 + y^2} \)
\( N_t(t, y) = 7 + \dfrac{1}{1 + y^2} \)
\( M_y(t, y) = N_t(t, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(t, y) = C \) fonksiyonu vardır.
\( F_t(t, y) = M(t, y) \)
\( F_y(t, y) = N(t, y) \)
\( N(t, y) \) fonksiyonunun \( y \) değişkenine göre integralini alarak \( F(t, y) \) fonksiyonunu bulalım.
\( F(t, y) = \displaystyle\int {N(t, y)\ dy} \)
\( = \displaystyle\int {\left( 7t + \dfrac{t}{1 + y^2} \right)\ dy} \)
\( y \) değişkenine göre alınan integralin \( t \) değişkenine bağlı integral sabitine \( h(t) \) diyelim.
\( = 7ty + t\arctan{y} + h(t) \)
\( h(t) \) fonksiyonunu bulmak için \( F(t, y) \) fonksiyonunun \( t \) değişkenine göre türevini alarak \( M(t, y) \) fonksiyonuna eşitleyelim.
\( F_t(t, y) = M(t, y) \)
\( 7y + \arctan{y} + h'(t) = 7y + \arctan{y} + e^{2t} \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( h'(t) \) aşağıdaki gibi bulunur.
\( h'(t) = e^{2t} \)
Tarafların \( t \) değişkenine göre integralini alalım.
\( \displaystyle\int {h'(t)\ dt} = \displaystyle\int {e^{2t}\ dt} \)
\( h(t) = \dfrac{e^{2t}}{2} \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(t, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( 7ty + t\arctan{y} + \dfrac{e^{2t}}{2} = C \)
\( x \gt 0 \) olmak üzere,
\( Ax^2e^y + \dfrac{7y}{x} + (x^3e^y + B\ln{x} + 1)y' = 0 \)
bir tam diferansiyel denklem olduğuna göre, denklemin genel çözümünü bulunuz.
Çözümü GösterDenklemi düzenleyelim.
\( Ax^2e^y + \dfrac{7y}{x} + (x^3e^y + B\ln{x} + 1)\dfrac{dy}{dx} = 0 \)
\( (Ax^2e^y + \dfrac{7y}{x})\ dx + (x^3e^y + B\ln{x} + 1)\ dy = 0 \)
\( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = Ax^2e^y + \dfrac{7y}{x} \)
\( N(x, y) = x^3e^y + B\ln{x} + 1 \)
Denklem tam olduğuna göre fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = Ax^2e^y + \dfrac{7}{x} \)
\( N_x(x, y) = 3x^2e^y + \dfrac{B}{x} \)
\( A = 3, \quad B = 7 \)
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( M(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} \)
\( = \displaystyle\int {(3x^2e^y + \dfrac{7y}{x})\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = x^3e^y + 7y\ln{x} + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, y) \) fonksiyonuna eşitleyelim.
\( F_y(x, y) = N(x, y) \)
\( x^3e^y + 7\ln{x} + g'(y) = x^3e^y + 7\ln{x} + 1 \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = 1 \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {1\ dy} \)
\( g(y) = y \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( x^3e^y + 7y\ln{x} + y = C \)
\( \left( \dfrac{3zx}{x^2 + 4} - 3x \right)\ dx + \left( \dfrac{3}{2}\ln(x^2 + 4) + ze^z \right)\ dz = 0 \)
\( z(2) = 0 \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterDenklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, z) = \dfrac{3zx}{x^2 + 4} - 3x \)
\( N(x, z) = \dfrac{3}{2}\ln(x^2 + 4) + ze^z \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_z(x, z) = N_x(x, z) \) eşitliği sağlanmalıdır.
\( M_z(x, z) = \dfrac{3x}{x^2 + 4} \)
\( N_x(x, z) = \dfrac{3x}{x^2 + 4} \)
\( M_z(x, z) = N_x(x, z) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, z) = C \) fonksiyonu vardır.
\( F_x(x, z) = M(x, z) \)
\( F_z(x, z) = N(x, z) \)
\( M(x, z) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, z) \) fonksiyonunu bulalım.
\( F(x, z) = \displaystyle\int {M(x, z)\ dx} \)
\( = \displaystyle\int {(\dfrac{3zx}{x^2 + 4} - 3x)\ dx} \)
\( x \) değişkenine göre alınan integralin \( z \) değişkenine bağlı integral sabitine \( g(z) \) diyelim.
\( = \dfrac{3z}{2}\ln(x^2 + 4) - \dfrac{3x^2}{2} + g(z) \)
\( g(z) \) fonksiyonunu bulmak için \( F(x, z) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, z) \) fonksiyonuna eşitleyelim.
\( F_z(x, z) = N(x, z) \)
\( \dfrac{3}{2}\ln(x^2 + 4) + g'(z) = \dfrac{3}{2}\ln(x^2 + 4) + ze^z \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(z) \) aşağıdaki gibi bulunur.
\( g'(z) = ze^z \)
Tarafların \( z \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(z)\ dz} = \displaystyle\int {ze^z\ dz} \)
İntegrali almak için kısmi integral yöntemini kullanalım.
\( g(z) = ze^z - e^z \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, z) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( \dfrac{3z}{2}\ln(x^2 + 4) - \dfrac{3x^2}{2} + ze^z - e^z = C \)
\( z(2) = 0 \) başlangıç değerini denklemde yerine koyalım.
\( \dfrac{3(0)}{2}\ln(2^2 + 4) - \dfrac{3(2)^2}{2} + 0e^0 - e^0 = C \)
\( 0 - 6 + 0 - 1 = C \)
\( C = -7 \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( \dfrac{3z}{2}\ln(x^2 + 4) - \dfrac{3x^2}{2} + ze^z - e^z = -7 \)
\( (e^y\sin(2x) + \sinh{x})\ dx - \left( \dfrac{e^y\cos(2x)}{2} + 3 \right)\ dy = 0 \)
\( y(0) = 0 \)
denkleminin verilen başlangıç değeri için çözümünü bulunuz.
Çözümü GösterDenklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = e^y\sin(2x) + \sinh{x} \)
\( N(x, y) = -\dfrac{e^y\cos(2x)}{2} - 3 \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = e^y\sin(2x) \)
\( N_x(x, y) = e^y\sin(2x) \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( M(x, y) \) fonksiyonunun \( x \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {M(x, y)\ dx} \)
\( = \displaystyle\int {(e^y\sin(2x) + \sinh{x})\ dx} \)
\( x \) değişkenine göre alınan integralin \( y \) değişkenine bağlı integral sabitine \( g(y) \) diyelim.
\( = -\dfrac{e^y\cos(2x)}{2} + \cosh{x} + g(y) \)
\( g(y) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( y \) değişkenine göre türevini alarak \( N(x, y) \) fonksiyonuna eşitleyelim.
\( F_y(x, y) = N(x, y) \)
\( -\dfrac{e^y\cos(2x)}{2} + g'(y) = -\dfrac{e^y\cos(2x)}{2} - 3 \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( g'(y) \) aşağıdaki gibi bulunur.
\( g'(y) = -3 \)
Tarafların \( y \) değişkenine göre integralini alalım.
\( \displaystyle\int {g'(y)\ dy} = \displaystyle\int {-3\ dy} \)
\( g(y) = -3y \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( -\dfrac{e^y\cos(2x)}{2} + \cosh{x} - 3y = C \)
\( y(0) = 0 \) başlangıç değerini denklemde yerine koyalım.
\( -\dfrac{e^0\cos(2(0))}{2} + \cosh{0} - 3(0) = C \)
\( -\dfrac{1}{2} + 1 - 0 = C \)
\( C = \dfrac{1}{2} \)
Denklemin verilen başlangıç değeri için çözümü aşağıdaki gibi bulunur.
\( -\dfrac{e^y\cos(2x)}{2} + \cosh{x} - 3y = \dfrac{1}{2} \)
\( (e^{3x} + 3x^2y)\ dx + (\sin{y} + x^3 + 2\ln{y})\ dy = 0 \)
denkleminin genel çözümünü bulunuz.
Çözümü GösterDenklemin bir tam diferansiyel denklem olup olmadığını anlamak için önce \( M \) ve \( N \) fonksiyonlarını belirleyelim.
\( M(x, y) = e^{3x} + 3x^2y \)
\( N(x, y) = \sin{y} + x^3 + 2\ln{y} \)
Denklemin tam olması için fonksiyonların kısmi türevleri arasında \( M_y(x, y) = N_x(x, y) \) eşitliği sağlanmalıdır.
\( M_y(x, y) = 3x^2 \)
\( N_x(x, y) = 3x^2 \)
\( M_y(x, y) = N_x(x, y) \) olduğu için verilen denklem bir tam diferansiyel denklemdir.
Buna göre aşağıdaki koşulları sağlayan ve verilen denklemin çözümü olan bir \( F(x, y) = C \) fonksiyonu vardır.
\( F_x(x, y) = M(x, y) \)
\( F_y(x, y) = N(x, y) \)
\( N(x, y) \) fonksiyonunun \( y \) değişkenine göre integralini alarak \( F(x, y) \) fonksiyonunu bulalım.
\( F(x, y) = \displaystyle\int {N(x, y)\ dy} \)
\( = \displaystyle\int {(\sin{y} + x^3 + 2\ln{y})\ dy} \)
\( y \) değişkenine göre alınan integralin \( x \) değişkenine bağlı integral sabitine \( h(x) \) diyelim.
\( \ln{y} \) ifadesinin integralini almak için kısmi integral alma yöntemini kullanalım.
\( = -\cos{y} + x^3y + 2y\ln{y} - 2y + h(x) \)
\( h(x) \) fonksiyonunu bulmak için \( F(x, y) \) fonksiyonunun \( x \) değişkenine göre türevini alarak \( M(x, y) \) fonksiyonuna eşitleyelim.
\( F_x(x, y) = M(x, y) \)
\( 3x^2y + h'(x) = e^{3x} + 3x^2y \)
Eşitliğin iki tarafındaki terimleri karşılaştırdığımızda \( h'(x) \) aşağıdaki gibi bulunur.
\( h'(x) = e^{3x} \)
Tarafların \( x \) değişkenine göre integralini alalım.
\( \displaystyle\int {h'(x)\ dx} = \displaystyle\int {e^{3x}\ dx} \)
\( h(x) = \dfrac{e^{3x}}{3} \)
Yöntemin en sonunda genel çözüme \( C \) sabiti ekleneceği için bu adımda ek bir integral sabiti eklemeye gerek yoktur.
Buna göre denklemin genel çözümü olan \( F(x, y) = C \) fonksiyonu aşağıdaki gibi bulunur.
\( \dfrac{e^{3x}}{3} - \cos{y} + x^3y + 2y\ln{y} - 2y = C \)