Euler Yöntemi
Analitik yöntem olarak adlandırılan yöntemler kullanılarak bir diferansiyel denklemin açık (\( y = y(x) \)) ya da kapalı (\( f(x, y) = c \)) formda kesin çözümü elde edilebilir ve bu çözüm kullanılarak herhangi bir \( x \) değeri için \( y \) değeri hesaplanabilir. Şu ana kadar incelediğimiz diferansiyel denklem çözüm yöntemlerinin tümü analitik yöntemlerdir.
Birkaç sebeple bir denklemin kesin çözümü elde edilemeyebilir. Birinci olarak, verilen denklemin çözümü için bir analitik yöntem bulunmayabilir. Aşağıdaki denklem buna bir örnek olarak verilebilir.
\( \dfrac{dy}{dx} = \sin(x^2 + y^2) \)
İkinci olarak, analitik bir yöntem mevcut olsa da çözüm adımlarında karşılaşılan bir integrali almak kolay ya da mümkün olmayabilir. Aşağıdaki integral ifadeleri buna birer örnek olarak verilebilir.
\( \displaystyle\int {e^{x^2}\ dx} \)
Üçüncü olarak, bir denklemin çözümü mümkün olsa da elde edilen kapalı formdaki çözümde belirli bir \( x \) değeri için \( y \) değerini hesaplamak kolay olmayabilir.
\( y + \ln{\abs{y}} = x \)
Kesin bir çözümün elde edilemediği bu gibi durumlarda nümerik yöntemlere başvurulur. Bir nümerik yöntemde \( y \) değerinin belirli bir \( x \) noktasındaki yaklaşık değeri bulunur.
Euler yöntemi, aşağıdaki formdaki başlangıç değer problemlerinde bilinmeyen \( y \) fonksiyonunun belirli bir noktadaki yaklaşık değerini bulmamızı sağlayan nümerik bir yöntemdir.
\( \dfrac{dy}{dx} = f(x, y) \)
\( y(x_0) = y_0 \)
\( \dfrac{dy}{dx} = 3x + 4y + 1 \)
\( y(1) = 5 \)
Euler yöntemi çoğu nümerik yöntem gibi yinelemeli bir yöntemdir ve türev konusunda gördüğümüz lineerleştirme yönteminin verilen diferansiyel denkleme tekrarlı şekilde uygulanmasından oluşur. Bu açıdan bu konunun öncesinde lineerleştirme mantığının ve formülünün iyi anlaşılması önemlidir.
Yukarıdaki formdaki bir başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x_n \) noktasındaki yaklaşık değerini bulmak için Euler yöntemi aşağıdaki şekilde uygulanabilir.
Adım 0: Adım büyüklüğü ve sayısı
\( x_0 \) noktasından \( x_n \) noktasına ulaşmak için \( x \) ekseni boyunca her adımdaki ilerleme miktarına adım büyüklüğü denir ve \( h \) ile gösterilir.
Verilen \( h \) değeri doğrultusunda yöntemin uygulanacağı adım sayısı aşağıdaki formülle belirlenir.
\( n = \dfrac{x_n - x_0}{h} \)
Adım 1: \( (x_1, y_1) \) noktasını bulma
Bir fonksiyona belirli bir noktada teğet olan doğrunun eğiminin fonksiyonun birinci türevine (\( \frac{dy}{dx} \)) eşit olduğunu biliyoruz.
Verilen denklemin formu gereği, bilinmeyen \( y \) fonksiyonu için bu eğim \( \frac{dy}{dx} = f(x, y(x)) \) olur, bu da başlangıç noktası için \( \frac{dy}{dx}|_{x=x_0} = f(x_0, y(x_0) = y_0) \) değerine eşittir.
\( y_0 \) başlangıç değeri olarak verildiği için \( f(x_0, y_0) \) eğimini hesaplayabiliriz.

Fonksiyonun \( x_1 \) noktasındaki yaklaşık değerini bulmak için lineerleştirme formülünü kullanalım. Bu formül \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak doğru üzerindeki \( x_1 \) noktası için \( y_1 \) değerini bulmamızı sağlar.
\( y_1 = y_0 + f(x_0, y_0)(x_1 - x_0) \)
Ardışık \( x \) noktaları arasındaki uzaklık adım büyüklüğüne eşittir (\( h = x_1 - x_0 \)).
\( y_1 = y_0 + hf(x_0, y_0) \)
Bu durumda \( y \) fonksiyonunun \( x_1 \) noktasındaki yaklaşık değeri olarak \( y_1 \) değeri bulunur.
\( y(x_1) \approx y_1 \)
Adım 2: \( (x_2, y_2) \) noktasını bulma
Benzer şekilde, \( y \) fonksiyonuna \( (x_1, y(x_1)) \) noktasında teğet olan doğrunun eğimi \( \frac{dy}{dx}|_{x=x_1} = f(x_1, y(x_1)) \) olur.
\( y \) fonksiyonu, dolayısıyla \( y(x_1) \) değeri bilinmediği için yerine yaklaşık değeri olan \( y_1 \) değerini, eğimin yaklaşık değeri olarak da \( f(x_1, y_1) \) değerini kullanabiliriz.
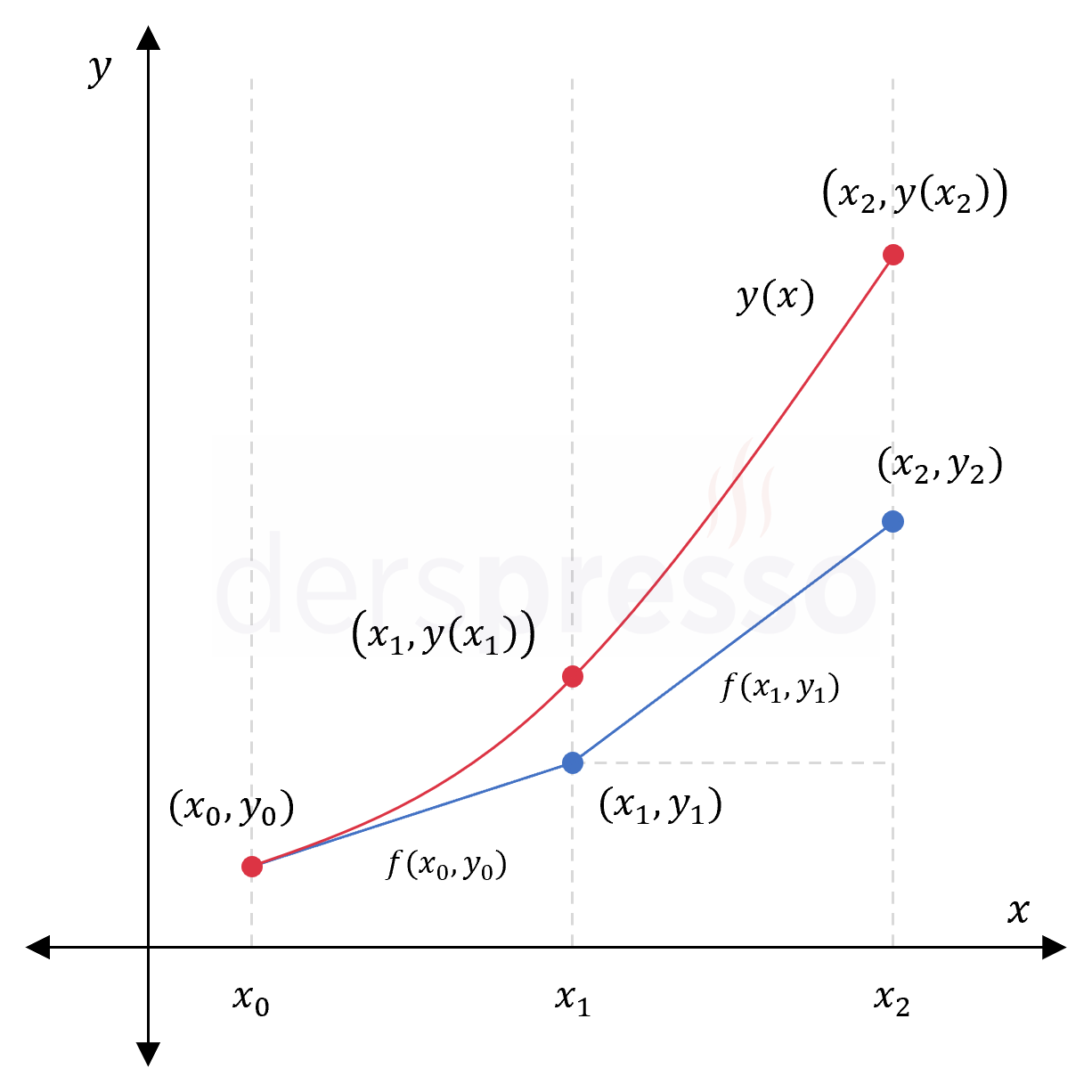
\( f(x_1, y(x_1)) \approx f(x_1, y_1) \)
Aynı lineerleştirme formülü ile, \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak doğru üzerindeki \( x_2 \) noktası için \( y_2 \) değerini bulalım.
\( y_2 = y_1 + f(x_1, y_1)(x_2 - x_1) \)
Ardışık \( x \) noktaları arasındaki uzaklık adım büyüklüğüne eşittir (\( h = x_2 - x_1 \)).
\( y_2 = y_1 + hf(x_1, y_1) \)
Bu durumda \( y \) fonksiyonunun \( x_2 \) noktasındaki yaklaşık değeri olarak \( y_2 \) değeri bulunur.
\( y(x_2) \approx y_2 \)
Adım 3: \( (x_{k+1}, y_{k+1}) \) noktasını bulma
2. adımda kullandığımız yaklaşımı sonraki adımlara uygulayarak, \( (x_k, y_k) \) noktasından geçen ve eğimi \( f(x_k, y_k) \) olan doğrunun denklemini kullanarak doğru üzerindeki \( x_{k+1} \) noktası için \( y_{k+1} \) değerini aşağıdaki formülle bulabiliriz.
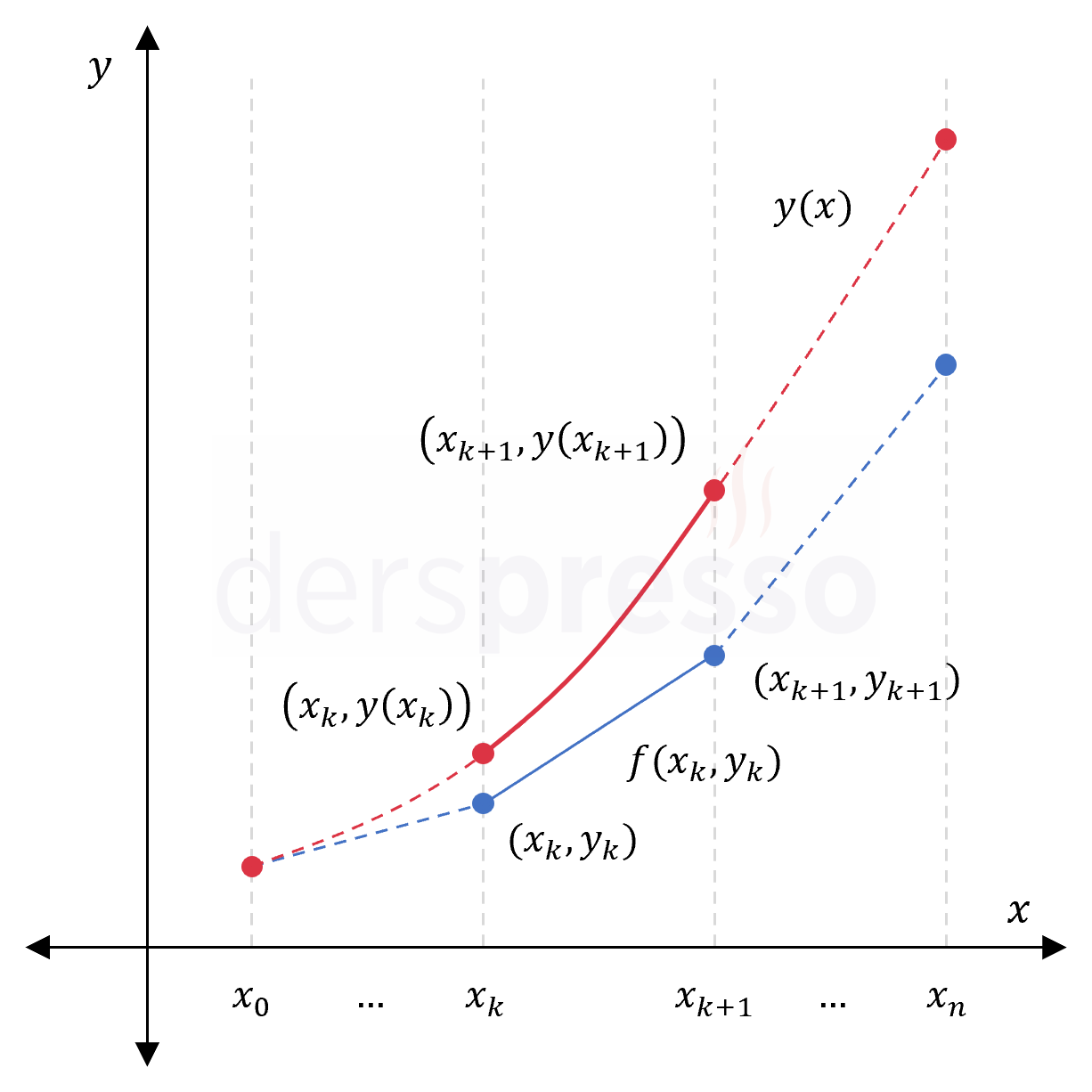
\( y_{k+1} = y_k + hf(x_k, y_k) \)
Bu durumda \( y \) fonksiyonunun \( x_{k+1} \) noktasındaki yaklaşık değeri olarak \( y_{k+1} \) değeri bulunur.
\( y(x_{k+1}) \approx y_{k+1} \)
Adım 4: \( (x_n, y_n) \) noktasını bulma
Bu yöntem \( n \) kez uygulandığında fonksiyonunun \( x_n \) noktasındaki yaklaşık değeri olarak \( y_n \) değeri bulunur.
\( y_n = y_{n-1} + hf(x_{n-1}, y_{n-1}) \)
\( y(x_n) \approx y_n \)
Euler yönteminin uygulamasını bir örnek üzerinde gösterelim.
\( y' = 3x^2 - 2x \)
\( y(1) = 1 \)
başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değerini \( h = \frac{1}{2} \) adım büyüklüğü kullanarak bulalım.
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 1, \quad y_0 = 1 \)
\( h = \frac{1}{2} \) adım büyüklüğü ile \( [1, 2] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{2 - 1}{\frac{1}{2}} = 2 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 3x_0^2 - 2x_0 = 3(1)^2 - 2(1) = 1 \)
\( x_1 = x_0 + h = 1 + \frac{1}{2} = \frac{3}{2} \)
\( y_1 = y_0 + hf(x_0, y_0) = 1 + \frac{1}{2}(1) = \frac{3}{2} \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 3x_1^2 - 2x_1 = 3(\frac{3}{2})^2 - 2(\frac{3}{2}) = \frac{15}{4} \)
\( x_2 = x_1 + h = \frac{3}{2} + \frac{1}{2} = 2 \)
\( y_2 = y_1 + hf(x_1, y_1) = \frac{3}{2} + \frac{1}{2}(\frac{15}{4}) = \frac{27}{8} \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( \frac{27}{8} \) olarak bulunur.
\( y(2) \approx y_2 = \frac{27}{8} \)
Aşağıdaki grafikte kırmızı renk (bilinmeyen) \( y \) fonksiyonunun gerçek grafiğini, mavi renk Euler yöntemi ile elde ettiğimiz doğruları ve yaklaşık değerleri temsil etmektedir.
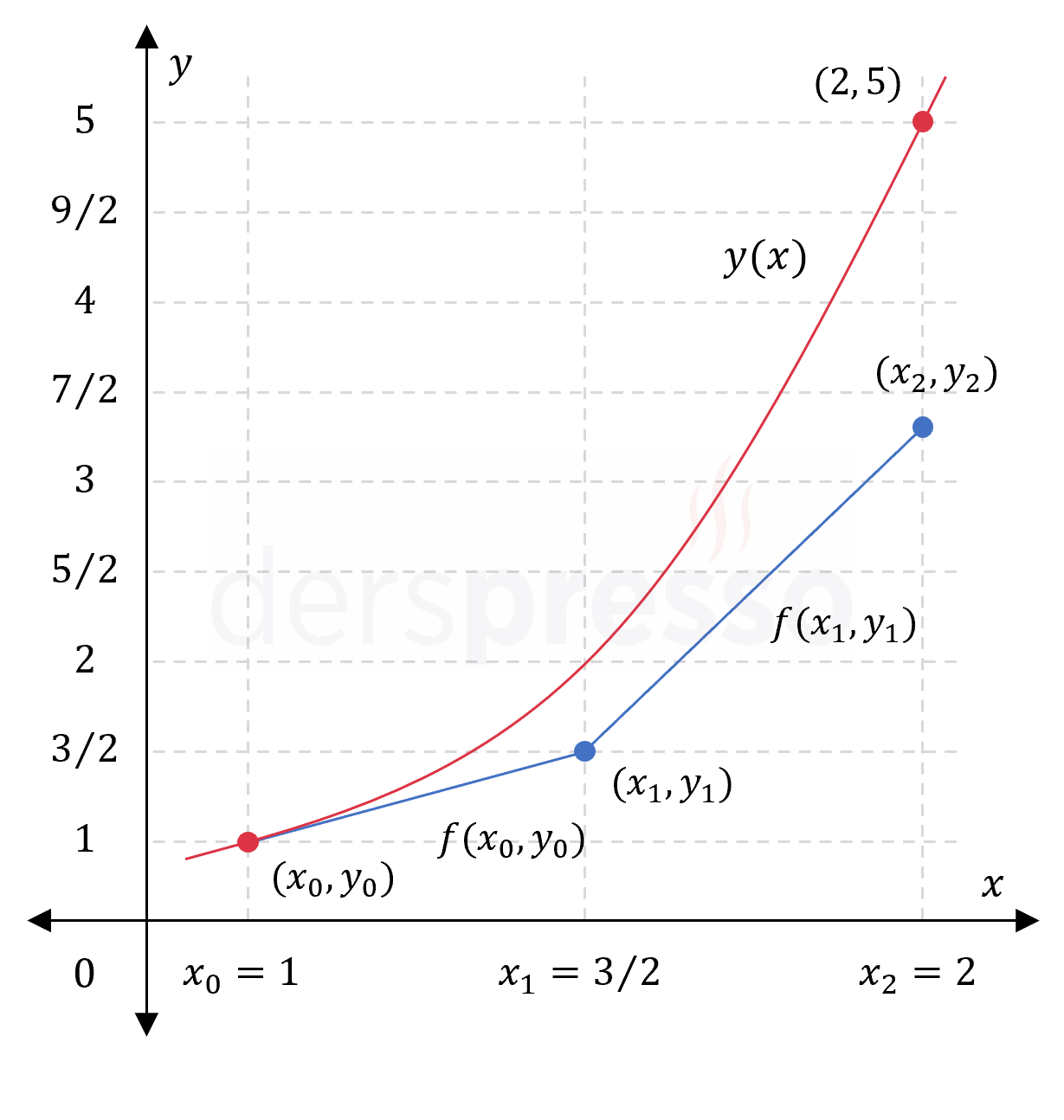
Şimdi de \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değerini \( h = \frac{1}{3} \) adım büyüklüğü kullanarak bulalım.
\( y' = 3x^2 - 2x \)
\( y(1) = 1 \)
başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değerini \( h = \frac{1}{3} \) adım büyüklüğü kullanarak bulalım.
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 1, \quad y_0 = 1 \)
\( h = \frac{1}{3} \) adım büyüklüğü ile \( [1, 2] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{2 - 1}{\frac{1}{3}} = 3 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 3x_0^2 - 2x_0 = 3(1)^2 - 2(1) = 1 \)
\( x_1 = x_0 + h = 1 + \frac{1}{3} = \frac{4}{3} \)
\( y_1 = y_0 + hf(x_0, y_0) = 1 + \frac{1}{3}(1) = \frac{4}{3} \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 3x_1^2 - 2x_1 = 3(\frac{4}{3})^2 - 2(\frac{4}{3}) = \frac{8}{3} \)
\( x_2 = x_1 + h = \frac{4}{3} + \frac{1}{3} = \frac{5}{3} \)
\( y_2 = y_1 + hf(x_1, y_1) = \frac{4}{3} + \frac{1}{3}(\frac{8}{3}) = \frac{20}{9} \)
Adım 3: \( (x_2, y_2) \) noktasından geçen ve eğimi \( f(x_2, y_2) \) olan doğrunun denklemini kullanarak \( (x_3, y_3) \) noktasının koordinatlarını bulalım.
\( f(x_2, y_2) = 3x_2^2 - 2x_2 = 3(\frac{5}{3})^2 - 2(\frac{5}{3}) = 5 \)
\( x_3 = x_2 + h = \frac{5}{3} + \frac{1}{3} = 2 \)
\( y_3 = y_2 + hf(x_2, y_2) = \frac{20}{9} + \frac{1}{3}(5) = \frac{35}{9} \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( \frac{35}{9} \) olarak bulunur.
\( y(2) \approx y_3 = \frac{35}{9} \)
Aşağıdaki grafikte yukarıdaki grafiğe ek olarak, yeşil renk Euler yöntemi ile elde ettiğimiz doğruları ve yaklaşık değerleri temsil etmektedir.
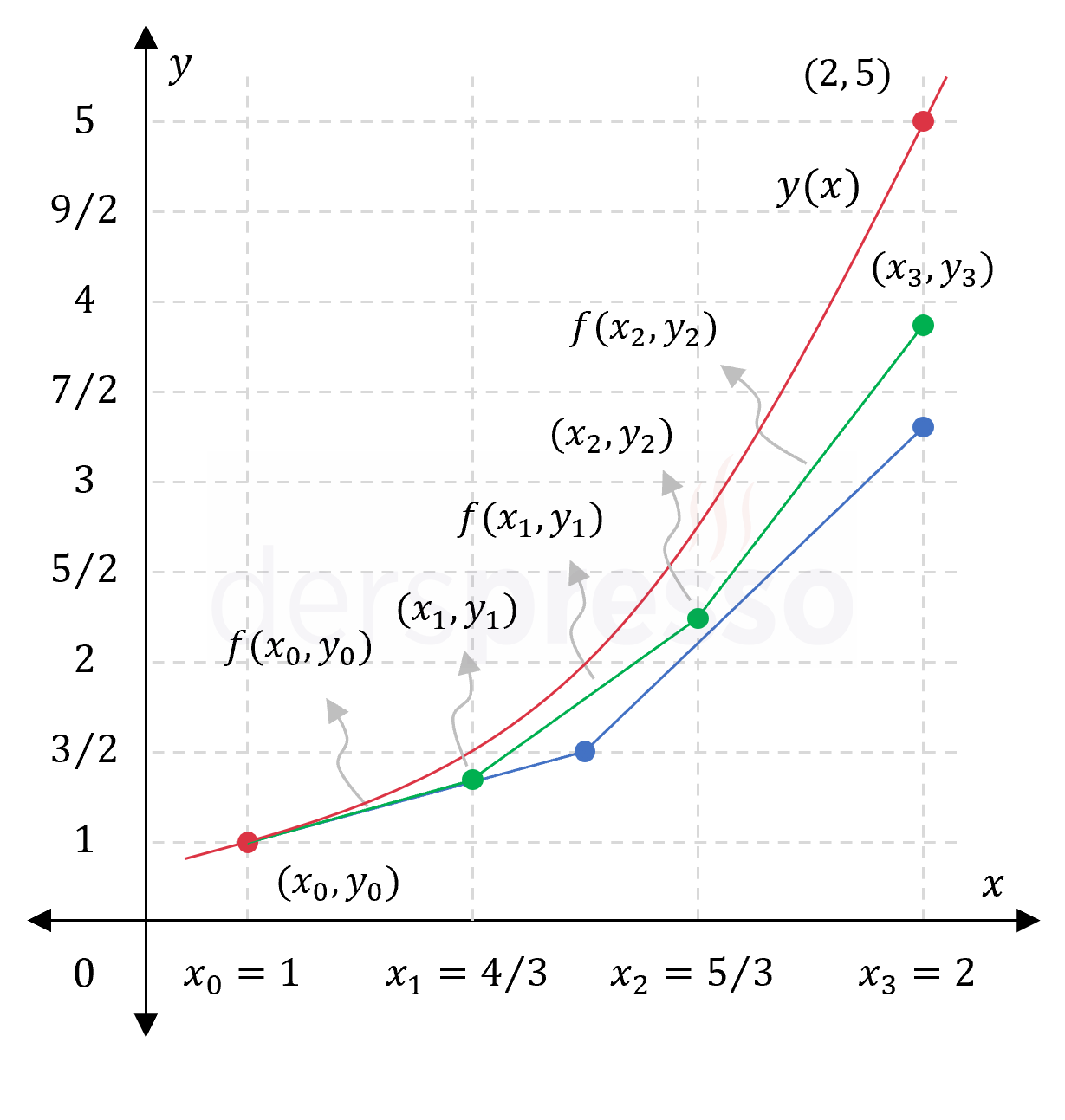
Bu örnekte adım büyüklüğünü küçülttüğümüzde (adım sayısını arttırdığımızda) fonksiyonun gerçek değerine daha yakın değerler elde ettiğimizi görebiliriz.
Şimdi de \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değerini \( h = \frac{1}{5} \) adım büyüklüğü kullanarak bulalım.
\( y' = 3x^2 - 2x \)
\( y(1) = 1 \)
başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değerini \( h = \frac{1}{5} \) adım büyüklüğü kullanarak bulalım.
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 1, \quad y_0 = 1 \)
\( h = \frac{1}{5} \) adım büyüklüğü ile \( [1, 2] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{2 - 1}{\frac{1}{5}} = 5 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 3x_0^2 - 2x_0 = 3(1)^2 - 2(1) = 1 \)
\( x_1 = x_0 + h = 1 + \frac{1}{5} = \frac{6}{5} \)
\( y_1 = y_0 + hf(x_0, y_0) = 1 + \frac{1}{5}(1) = \frac{6}{5} \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 3x_1^2 - 2x_1 = 3(\frac{6}{5})^2 - 2(\frac{6}{5}) = \frac{48}{25} \)
\( x_2 = x_1 + h = \frac{6}{5} + \frac{1}{5} = \frac{7}{5} \)
\( y_2 = y_1 + hf(x_1, y_1) = \frac{6}{5} + \frac{1}{5}(\frac{48}{25}) = \frac{198}{125} \)
Adım 3: \( (x_2, y_2) \) noktasından geçen ve eğimi \( f(x_2, y_2) \) olan doğrunun denklemini kullanarak \( (x_3, y_3) \) noktasının koordinatlarını bulalım.
\( f(x_2, y_2) = 3x_2^2 - 2x_2 = 3(\frac{7}{5})^2 - 2(\frac{7}{5}) = \frac{77}{25} \)
\( x_3 = x_2 + h = \frac{7}{5} + \frac{1}{5} = \frac{8}{5} \)
\( y_3 = y_2 + hf(x_2, y_2) = \frac{198}{125} + \frac{1}{5}(\frac{77}{25}) = \frac{11}{5} \)
Adım 4: \( (x_3, y_3) \) noktasından geçen ve eğimi \( f(x_3, y_3) \) olan doğrunun denklemini kullanarak \( (x_4, y_4) \) noktasının koordinatlarını bulalım.
\( f(x_3, y_3) = 3x_3^2 - 2x_3 = 3(\frac{8}{5})^2 - 2(\frac{8}{5}) = \frac{112}{25} \)
\( x_4 = x_3 + h = \frac{8}{5} + \frac{1}{5} = \frac{9}{5} \)
\( y_4 = y_3 + hf(x_3, y_3) = \frac{11}{5} + \frac{1}{5}(\frac{112}{25}) = \frac{387}{125} \)
Adım 5: \( (x_4, y_4) \) noktasından geçen ve eğimi \( f(x_4, y_4) \) olan doğrunun denklemini kullanarak \( (x_5, y_5) \) noktasının koordinatlarını bulalım.
\( f(x_4, y_4) = 3x_4^2 - 2x_4 = 3(\frac{9}{5})^2 - 2(\frac{9}{5}) = \frac{153}{25} \)
\( x_5 = x_4 + h = \frac{9}{5} + \frac{1}{5} = 2 \)
\( y_5 = y_4 + hf(x_4, y_4) = \frac{387}{125} + \frac{1}{5}(\frac{153}{25}) = \frac{108}{25} \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( \frac{108}{25} \) olarak bulunur.
\( y(2) \approx y_5 = \frac{108}{25} \)
Aşağıdaki grafikte yukarıdaki grafiğe ek olarak, mor renk Euler yöntemi ile elde ettiğimiz doğruları ve yaklaşık değerleri temsil etmektedir.
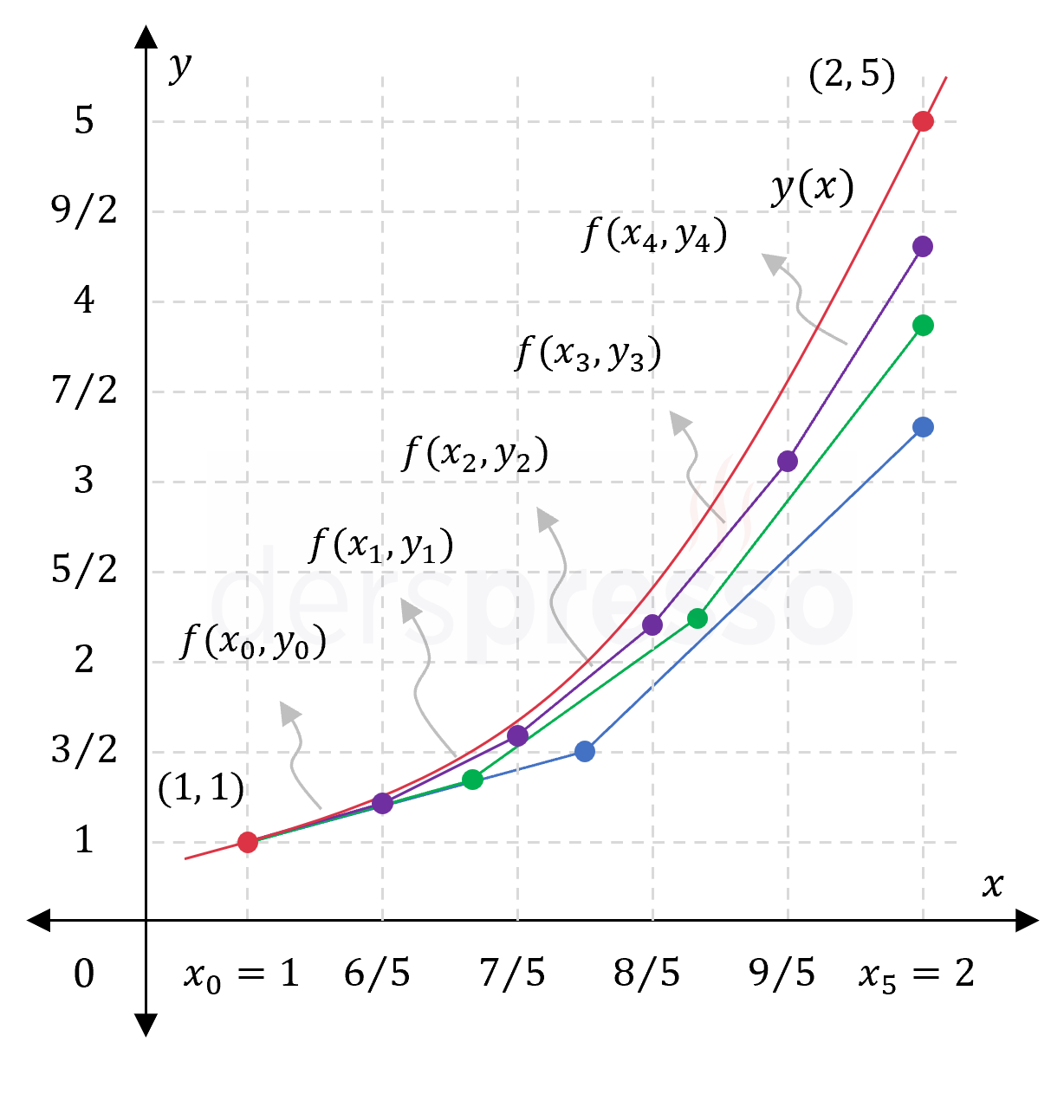
Bu örnekte adım büyüklüğünü daha da küçülttüğümüzde (adım sayısını arttırdığımızda) fonksiyonun gerçek değerine önceki iki örnekten daha yakın değerler elde ettiğimizi görebiliriz.
Yukarıdaki örneklerde gördüğümüz (ve tahmin edebileceğimiz) üzere, daha küçük adım büyüklükleri seçildikçe Euler yöntemi fonksiyonun gerçek değerine daha yakın yaklaşık değerler üretir. Bunun bir sonucu olarak, (gerekli süreklilik koşulları sağlandığı sürece) \( x_n \) noktası için hesapladığımız yaklaşık değerin adım büyüklüğü sıfıra giderkenki (adım sayısı sonsuza giderkenki) limiti fonksiyonun bu noktadaki gerçek değerine eşit olur.
\( \lim\limits_{h \to 0} {y_n} = y(x_n) \)
\( \lim\limits_{n \to \infty} {y_n} = y(x_n) \)
Nümerik yöntemlerde \( y \) fonksiyonu bilinmediği için, bu yöntem ile bulunan yaklaşık değerlerin gerçek değerlere ne kadar yakın olduğunun gerçek hayat problemlerinde bilinemeyeceğini vurgulamamız gerekir.
\( y' = 4x \)
\( y(1) = 0 \)
başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değerini aşağıdaki adım büyüklüklerini kullanarak bulunuz.
(a) \( h = \dfrac{1}{2} \)
(b) \( h = \dfrac{1}{3} \)
(c) \( h = \dfrac{1}{4} \)
Çözümü Göster(a) seçeneği:
\( h = \dfrac{1}{2} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 1, \quad y_0 = 0 \)
\( h = \frac{1}{2} \) adım büyüklüğü ile \( [1, 2] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{2 - 1}{\frac{1}{2}} = 2 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 4x_0 = 4(1) = 4 \)
\( x_1 = x_0 + h = 1 + \dfrac{1}{2} = \dfrac{3}{2} \)
\( y_1 = y_0 + hf(x_0, y_0) = 0 + \dfrac{1}{2}(4) = 2 \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 4x_1 = 4(\dfrac{3}{2}) = 6 \)
\( x_2 = x_1 + h = \dfrac{3}{2} + \dfrac{1}{2} = 2 \)
\( y_2 = y_1 + hf(x_1, y_1) = 2 + \dfrac{1}{2}(6) = 5 \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( 5 \) olarak bulunur.
\( y(2) \approx y_2 = 5 \)
(b) seçeneği:
\( h = \dfrac{1}{3} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 1, \quad y_0 = 0 \)
\( h = \frac{1}{3} \) adım büyüklüğü ile \( [1, 2] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{2 - 1}{\frac{1}{3}} = 3 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 4x_0 = 4(1) = 4 \)
\( x_1 = x_0 + h = 1 + \dfrac{1}{3} = \dfrac{4}{3} \)
\( y_1 = y_0 + hf(x_0, y_0) = 0 + \dfrac{1}{3}(4) = \dfrac{4}{3} \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 4x_1 = 4(\dfrac{4}{3}) = \dfrac{16}{3} \)
\( x_2 = x_1 + h = \dfrac{4}{3} + \dfrac{1}{3} = \dfrac{5}{3} \)
\( y_2 = y_1 + hf(x_1, y_1) = \dfrac{4}{3} + \dfrac{1}{3}(\dfrac{16}{3}) = \dfrac{28}{9} \)
Adım 3: \( (x_2, y_2) \) noktasından geçen ve eğimi \( f(x_2, y_2) \) olan doğrunun denklemini kullanarak \( (x_3, y_3) \) noktasının koordinatlarını bulalım.
\( f(x_2, y_2) = 4x_2 = 4(\dfrac{5}{3}) = \dfrac{20}{3} \)
\( x_3 = x_2 + h = \dfrac{5}{3} + \dfrac{1}{3} = 2 \)
\( y_3 = y_2 + hf(x_2, y_2) = \dfrac{28}{9} + \dfrac{1}{3}(\dfrac{20}{3}) = \dfrac{48}{9} \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( \frac{48}{9} \) olarak bulunur.
\( y(2) \approx y_3 = \dfrac{48}{9} \)
(c) seçeneği:
\( h = \dfrac{1}{4} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 1, \quad y_0 = 0 \)
\( h = \frac{1}{4} \) adım büyüklüğü ile \( [1, 2] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{2 - 1}{\frac{1}{4}} = 4 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 4x_0 = 4(1) = 4 \)
\( x_1 = x_0 + h = 1 + \dfrac{1}{4} = \dfrac{5}{4} \)
\( y_1 = y_0 + hf(x_0, y_0) = 0 + \dfrac{1}{4}(4) = 1 \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 4x_1 = 4(\dfrac{5}{4}) = 5 \)
\( x_2 = x_1 + h = \dfrac{5}{4} + \dfrac{1}{4} = \dfrac{3}{2} \)
\( y_2 = y_1 + hf(x_1, y_1) = 1 + \dfrac{1}{4}(5) = \dfrac{9}{4} \)
Adım 3: \( (x_2, y_2) \) noktasından geçen ve eğimi \( f(x_2, y_2) \) olan doğrunun denklemini kullanarak \( (x_3, y_3) \) noktasının koordinatlarını bulalım.
\( f(x_2, y_2) = 4x_2 = 4(\dfrac{3}{2}) = 6 \)
\( x_3 = x_2 + h = \dfrac{3}{2} + \dfrac{1}{4} = \dfrac{7}{4} \)
\( y_3 = y_2 + hf(x_2, y_2) = \dfrac{9}{4} + \dfrac{1}{4}(6) = \dfrac{15}{4} \)
Adım 4: \( (x_3, y_3) \) noktasından geçen ve eğimi \( f(x_3, y_3) \) olan doğrunun denklemini kullanarak \( (x_4, y_4) \) noktasının koordinatlarını bulalım.
\( f(x_3, y_3) = 4x_3 = 4(\dfrac{7}{4}) = 7 \)
\( x_4 = x_3 + h = \dfrac{7}{4} + \dfrac{1}{4} = 2 \)
\( y_4 = y_3 + hf(x_3, y_3) = \dfrac{15}{4} + \dfrac{1}{4}(7) = \dfrac{11}{2} \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( \frac{11}{2} \) olarak bulunur.
\( y(2) \approx y_4 = \dfrac{11}{2} \)
\( y' = 3 - 2x + y \)
\( y(2) = 1 \)
başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x = 4 \) noktasındaki yaklaşık değerini aşağıdaki adım büyüklüklerini kullanarak bulunuz.
(a) \( h = 1 \)
(b) \( h = \dfrac{1}{2} \)
(c) \( h = \dfrac{1}{3} \)
Çözümü Göster(a) seçeneği:
\( h = 1 \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 2, \quad y_0 = 1 \)
\( h = 1 \) adım büyüklüğü ile \( [2, 4] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{4 - 2}{1} = 2 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 3 - 2x_0 + y_0 = 3 - 2(2) + 1 = 0 \)
\( x_1 = x_0 + h = 2 + 1 = 3 \)
\( y_1 = y_0 + hf(x_0, y_0) = 1 + 1(0) = 1 \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 3 - 2x_1 + y_1 = 3 - 2(3) + 2 = -2 \)
\( x_2 = x_1 + h = 3 + 1 = 4 \)
\( y_2 = y_1 + hf(x_1, y_1) = 1 + 1(-2) = -1 \)
Buna göre \( y \) fonksiyonunun \( x = 4 \) noktasındaki yaklaşık değeri \( -1 \) olarak bulunur.
\( y(4) \approx y_2 = -1 \)
(b) seçeneği:
\( h = \dfrac{1}{2} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 2, \quad y_0 = 1 \)
\( h = \frac{1}{2} \) adım büyüklüğü ile \( [2, 4] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{4 - 2}{\frac{1}{2}} = 4 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 3 - 2x_0 + y_0 = 3 - 2(2) + 1 = 0 \)
\( x_1 = x_0 + h = 2 + \dfrac{1}{2} = \dfrac{5}{2} \)
\( y_1 = y_0 + hf(x_0, y_0) = 1 + \dfrac{1}{2}(0) = 1 \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 3 - 2x_1 + y_1 = 3 - 2(\dfrac{5}{2}) + 1 = -1 \)
\( x_2 = x_1 + h = \dfrac{5}{2} + \dfrac{1}{2} = 3 \)
\( y_2 = y_1 + hf(x_1, y_1) = 1 + \dfrac{1}{2}(-1) = \dfrac{1}{2} \)
Adım 3: \( (x_2, y_2) \) noktasından geçen ve eğimi \( f(x_2, y_2) \) olan doğrunun denklemini kullanarak \( (x_3, y_3) \) noktasının koordinatlarını bulalım.
\( f(x_2, y_2) = 3 - 2x_2 + y_2 = 3 - 2(3) + \dfrac{1}{2} = -\dfrac{5}{2} \)
\( x_3 = x_2 + h = 3 + \dfrac{1}{2} = \dfrac{7}{2} \)
\( y_3 = y_2 + hf(x_2, y_2) = \dfrac{1}{2} + \dfrac{1}{2}(-\dfrac{5}{2}) = -\dfrac{3}{4} \)
Adım 4: \( (x_3, y_3) \) noktasından geçen ve eğimi \( f(x_3, y_3) \) olan doğrunun denklemini kullanarak \( (x_4, y_4) \) noktasının koordinatlarını bulalım.
\( f(x_3, y_3) = 3 - 2x_3 + y_3 = 3 - 2(\dfrac{7}{2}) + (-\dfrac{3}{4}) = -\dfrac{19}{4} \)
\( x_4 = x_3 + h = \dfrac{7}{2} + \dfrac{1}{2} = 4 \)
\( y_4 = y_3 + hf(x_3, y_3) = -\dfrac{3}{4} + \dfrac{1}{2}(-\dfrac{19}{4}) = -\dfrac{25}{8} \)
Buna göre \( y \) fonksiyonunun \( x = 4 \) noktasındaki yaklaşık değeri \( -\frac{25}{8} \) olarak bulunur.
\( y(4) \approx y_4 = -\dfrac{25}{8} \)
(c) seçeneği:
\( h = \dfrac{1}{3} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 2, \quad y_0 = 1 \)
\( h = \frac{1}{3} \) adım büyüklüğü ile \( [2, 4] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{4 - 2}{\frac{1}{3}} = 6 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 3 - 2x_0 + y_0 = 3 - 2(2) + 1 = 0 \)
\( x_1 = x_0 + h = 2 + \dfrac{1}{3} = \dfrac{7}{3} \)
\( y_1 = y_0 + hf(x_0, y_0) = 1 + \dfrac{1}{3}(0) = 1 \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 3 - 2x_1 + y_1 = 3 - 2(\dfrac{7}{3}) + 1 = -\dfrac{2}{3} \)
\( x_2 = x_1 + h = \dfrac{7}{3} + \dfrac{1}{3} = \dfrac{8}{3} \)
\( y_2 = y_1 + hf(x_1, y_1) = 1 + \dfrac{1}{3}(-\dfrac{2}{3}) = \dfrac{7}{9} \)
Adım 3: \( (x_2, y_2) \) noktasından geçen ve eğimi \( f(x_2, y_2) \) olan doğrunun denklemini kullanarak \( (x_3, y_3) \) noktasının koordinatlarını bulalım.
\( f(x_2, y_2) = 3 - 2x_2 + y_2 = 3 - 2(\dfrac{8}{3}) + \dfrac{7}{9} = -\dfrac{14}{9} \)
\( x_3 = x_2 + h = \dfrac{8}{3} + \dfrac{1}{3} = 3 \)
\( y_3 = y_2 + hf(x_2, y_2) = \dfrac{7}{9} + \dfrac{1}{3}(-\dfrac{14}{9}) = \dfrac{7}{27} \)
Adım 4: \( (x_3, y_3) \) noktasından geçen ve eğimi \( f(x_3, y_3) \) olan doğrunun denklemini kullanarak \( (x_4, y_4) \) noktasının koordinatlarını bulalım.
\( f(x_3, y_3) = 3 - 2x_3 + y_3 = 3 - 2(3) + \dfrac{7}{27} = -\dfrac{74}{27} \)
\( x_4 = x_3 + h = 3 + \dfrac{1}{3} = \dfrac{10}{3} \)
\( y_4 = y_3 + hf(x_3, y_3) = \dfrac{7}{27} + \dfrac{1}{3}(-\dfrac{74}{27}) = -\dfrac{53}{81} \)
Adım 5: \( (x_4, y_4) \) noktasından geçen ve eğimi \( f(x_4, y_4) \) olan doğrunun denklemini kullanarak \( (x_5, y_5) \) noktasının koordinatlarını bulalım.
\( f(x_4, y_4) = 3 - 2x_4 + y_4 = 3 - 2(\dfrac{10}{3}) + (-\dfrac{53}{81}) = -\dfrac{350}{81} \)
\( x_5 = x_4 + h = \dfrac{10}{3} + \dfrac{1}{3} = \dfrac{11}{3} \)
\( y_5 = y_4 + hf(x_4, y_4) = -\dfrac{53}{81} + \dfrac{1}{3}(-\dfrac{350}{81}) = -\dfrac{509}{243} \)
Adım 6: \( (x_5, y_5) \) noktasından geçen ve eğimi \( f(x_5, y_5) \) olan doğrunun denklemini kullanarak \( (x_6, y_6) \) noktasının koordinatlarını bulalım.
\( f(x_5, y_5) = 3 - 2x_5 + y_5 = 3 - 2(\dfrac{11}{3}) + (-\dfrac{509}{243}) = -\dfrac{1562}{243} \)
\( x_6 = x_5 + h = \dfrac{11}{3} + \dfrac{1}{3} = 4 \)
\( y_6 = y_5 + hf(x_5, y_5) = (-\dfrac{509}{243}) + \dfrac{1}{3}(-\dfrac{1562}{243}) = -\dfrac{3089}{729} \)
Buna göre \( y \) fonksiyonunun \( x = 4 \) noktasındaki yaklaşık değeri \( -\frac{3089}{729} \) olarak bulunur.
\( y(4) \approx y_6 = -\dfrac{3089}{729} \)
\( y' = x^2 - y \)
\( y(0) = -1 \)
başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x = 1 \) noktasındaki yaklaşık değerini aşağıdaki adım büyüklüklerini kullanarak bulunuz.
(a) \( h = \dfrac{1}{2} \)
(b) \( h = \dfrac{1}{3} \)
(c) \( h = \dfrac{1}{4} \)
Çözümü Göster(a) seçeneği:
\( h = \dfrac{1}{2} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 0, \quad y_0 = -1 \)
\( h = \frac{1}{2} \) adım büyüklüğü ile \( [0, 1] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{1 - 0}{\frac{1}{2}} = 2 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = x_0^2 - y_0 = 0^2 - (-1) = 1 \)
\( x_1 = x_0 + h = 0 + \dfrac{1}{2} = \dfrac{1}{2} \)
\( y_1 = y_0 + hf(x_0, y_0) = -1 + \dfrac{1}{2}(1) = -\dfrac{1}{2} \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = x_1^2 - y_1 = (\dfrac{1}{2})^2 - (-\dfrac{1}{2}) = \dfrac{3}{4} \)
\( x_2 = x_1 + h = \dfrac{1}{2} + \dfrac{1}{2} = 1 \)
\( y_2 = y_1 + hf(x_1, y_1) = -\dfrac{1}{2} + \dfrac{1}{2}(\dfrac{3}{4}) = -\dfrac{1}{8} \)
Buna göre \( y \) fonksiyonunun \( x = 1 \) noktasındaki yaklaşık değeri \( -\frac{1}{8} \) olarak bulunur.
\( y(1) \approx y_2 = -\dfrac{1}{8} \)
(b) seçeneği:
\( h = \dfrac{1}{3} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 0, \quad y_0 = -1 \)
\( h = \frac{1}{3} \) adım büyüklüğü ile \( [0, 1] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{1 - 0}{\frac{1}{3}} = 3 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = x_0^2 - y_0 = 0^2 - (-1) = 1 \)
\( x_1 = x_0 + h = 0 + \dfrac{1}{3} = \dfrac{1}{3} \)
\( y_1 = y_0 + hf(x_0, y_0) = -1 + \dfrac{1}{3}(1) = -\dfrac{2}{3} \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = x_1^2 - y_1 = (\dfrac{1}{3})^2 - (-\dfrac{2}{3}) = \dfrac{7}{9} \)
\( x_2 = x_1 + h = \dfrac{1}{3} + \dfrac{1}{3} = \dfrac{2}{3} \)
\( y_2 = y_1 + hf(x_1, y_1) = -\dfrac{2}{3} + \dfrac{1}{3}(\dfrac{7}{9}) = -\dfrac{11}{27} \)
Adım 3: \( (x_2, y_2) \) noktasından geçen ve eğimi \( f(x_2, y_2) \) olan doğrunun denklemini kullanarak \( (x_3, y_3) \) noktasının koordinatlarını bulalım.
\( f(x_2, y_2) = x_2^2 - y_2 = (\dfrac{2}{3})^2 - (-\dfrac{11}{27}) = \dfrac{23}{27} \)
\( x_3 = x_2 + h = \dfrac{2}{3} + \dfrac{1}{3} = 1 \)
\( y_3 = y_2 + hf(x_2, y_2) = -\dfrac{11}{27} + \dfrac{1}{3}(\dfrac{23}{27}) = -\dfrac{10}{81} \)
Buna göre \( y \) fonksiyonunun \( x = 1 \) noktasındaki yaklaşık değeri \( -\frac{10}{81} \) olarak bulunur.
\( y(1) \approx y_3 = -\dfrac{10}{81} \)
(c) seçeneği:
\( h = \dfrac{1}{4} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 0, \quad y_0 = -1 \)
\( h = \frac{1}{4} \) adım büyüklüğü ile \( [0, 1] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{1 - 0}{\frac{1}{4}} = 4 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = x_0^2 - y_0 = 0^2 - (-1) = 1 \)
\( x_1 = x_0 + h = 0 + \dfrac{1}{4} = \dfrac{1}{4} \)
\( y_1 = y_0 + hf(x_0, y_0) = -1 + \dfrac{1}{4}(1) = -\dfrac{3}{4} \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = x_1^2 - y_1 = (\dfrac{1}{4})^2 - (-\dfrac{3}{4}) = \dfrac{13}{16} \)
\( x_2 = x_1 + h = \dfrac{1}{4} + \dfrac{1}{4} = \dfrac{1}{2} \)
\( y_2 = y_1 + hf(x_1, y_1) = -\dfrac{3}{4} + \dfrac{1}{4}(\dfrac{13}{16}) = -\dfrac{35}{64} \)
Adım 3: \( (x_2, y_2) \) noktasından geçen ve eğimi \( f(x_2, y_2) \) olan doğrunun denklemini kullanarak \( (x_3, y_3) \) noktasının koordinatlarını bulalım.
\( f(x_2, y_2) = x_2^2 - y_2 = (\dfrac{1}{2})^2 - (-\dfrac{35}{64}) = \dfrac{51}{64} \)
\( x_3 = x_2 + h = \dfrac{1}{2} + \dfrac{1}{4} = \dfrac{3}{4} \)
\( y_3 = y_2 + hf(x_2, y_2) = -\dfrac{35}{64} + \dfrac{1}{4}(\dfrac{51}{64}) = -\dfrac{89}{256} \)
Adım 4: \( (x_3, y_3) \) noktasından geçen ve eğimi \( f(x_3, y_3) \) olan doğrunun denklemini kullanarak \( (x_4, y_4) \) noktasının koordinatlarını bulalım.
\( f(x_3, y_3) = x_3^2 - y_3 = (\dfrac{3}{4})^2 - (-\dfrac{89}{256}) = \dfrac{233}{256} \)
\( x_4 = x_3 + h = \dfrac{3}{4} + \dfrac{1}{4} = 1 \)
\( y_4 = y_3 + hf(x_3, y_3) = -\dfrac{89}{256} + \dfrac{1}{4}(\dfrac{233}{256}) = -\dfrac{123}{1024} \)
Buna göre \( y \) fonksiyonunun \( x = 1 \) noktasındaki yaklaşık değeri \( -\frac{123}{1024} \) olarak bulunur.
\( y(1) \approx y_4 = -\dfrac{123}{1024} \)
\( y' = 5xy \)
\( y(0) = 1 \)
başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x = 1 \) noktasındaki yaklaşık değerini aşağıdaki adım büyüklüklerini kullanarak bulunuz.
(a) \( h = \dfrac{1}{2} \)
(b) \( h = \dfrac{1}{3} \)
(c) \( h = \dfrac{1}{5} \)
Çözümü Göster(a) seçeneği:
\( h = \dfrac{1}{2} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 0, \quad y_0 = 1 \)
\( h = \dfrac{1}{2} \) adım büyüklüğü ile \( [0, 1] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{1 - 0}{\frac{1}{2}} = 2 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 5x_0y_0 = 5(0)(1) = 0 \)
\( x_1 = x_0 + h = 0 + \dfrac{1}{2} = \dfrac{1}{2} \)
\( y_1 = y_0 + hf(x_0, y_0) = 1 + \dfrac{1}{2}(0) = 1 \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 5x_1y_1 = 5(\dfrac{1}{2})(1) = \dfrac{5}{2} \)
\( x_2 = x_1 + h = \dfrac{1}{2} + \dfrac{1}{2} = 1 \)
\( y_2 = y_1 + hf(x_1, y_1) = 1 + \dfrac{1}{2}(\dfrac{5}{2}) = \dfrac{9}{4} \)
Buna göre \( y \) fonksiyonunun \( x = 1 \) noktasındaki yaklaşık değeri \( \frac{9}{4} \) olarak bulunur.
\( y(1) \approx y_2 = \dfrac{9}{4} \)
(b) seçeneği:
\( h = \dfrac{1}{3} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 0, \quad y_0 = 1 \)
\( h = \dfrac{1}{3} \) adım büyüklüğü ile \( [0, 1] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{1 - 0}{\frac{1}{3}} = 3 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 5x_0y_0 = 5(0)(1) = 0 \)
\( x_1 = x_0 + h = 0 + \dfrac{1}{3} = \dfrac{1}{3} \)
\( y_1 = y_0 + hf(x_0, y_0) = 1 + \dfrac{1}{3}(0) = 1 \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 5x_1y_1 = 5(\dfrac{1}{3})(1) = \dfrac{5}{3} \)
\( x_2 = x_1 + h = \dfrac{1}{3} + \dfrac{1}{3} = \dfrac{2}{3} \)
\( y_2 = y_1 + hf(x_1, y_1) = 1 + \dfrac{1}{3}(\dfrac{5}{3}) = \dfrac{14}{9} \)
Adım 3: \( (x_2, y_2) \) noktasından geçen ve eğimi \( f(x_2, y_2) \) olan doğrunun denklemini kullanarak \( (x_3, y_3) \) noktasının koordinatlarını bulalım.
\( f(x_2, y_2) = 5x_2y_2 = 5(\dfrac{2}{3})(\dfrac{14}{9}) = \dfrac{140}{27} \)
\( x_3 = x_2 + h = \dfrac{2}{3} + \dfrac{1}{3} = 1 \)
\( y_3 = y_2 + hf(x_2, y_2) = \dfrac{14}{9} + \dfrac{1}{3}(\dfrac{140}{27}) = \dfrac{266}{81} \)
Buna göre \( y \) fonksiyonunun \( x = 1 \) noktasındaki yaklaşık değeri \( \frac{266}{81} \) olarak bulunur.
\( y(1) \approx y_3 = \dfrac{266}{81} \)
(c) seçeneği:
\( h = \dfrac{1}{5} \)
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 0, \quad y_0 = 1 \)
\( h = \dfrac{1}{5} \) adım büyüklüğü ile \( [0, 1] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{1 - 0}{\frac{1}{5}} = 5 \)
Adım 1: \( (x_0, y_0) \) noktasından geçen ve eğimi \( f(x_0, y_0) \) olan doğrunun denklemini kullanarak \( (x_1, y_1) \) noktasının koordinatlarını bulalım.
\( f(x_0, y_0) = 5x_0y_0 = 5(0)(1) = 0 \)
\( x_1 = x_0 + h = 0 + \dfrac{1}{5} = \dfrac{1}{5} \)
\( y_1 = y_0 + hf(x_0, y_0) = 1 + \dfrac{1}{5}(0) = 1 \)
Adım 2: \( (x_1, y_1) \) noktasından geçen ve eğimi \( f(x_1, y_1) \) olan doğrunun denklemini kullanarak \( (x_2, y_2) \) noktasının koordinatlarını bulalım.
\( f(x_1, y_1) = 5x_1y_1 = 5(\dfrac{1}{5})(1) = 1 \)
\( x_2 = x_1 + h = \dfrac{1}{5} + \dfrac{1}{5} = \dfrac{2}{5} \)
\( y_2 = y_1 + hf(x_1, y_1) = 1 + \dfrac{1}{5}(1) = \dfrac{6}{5} \)
Adım 3: \( (x_2, y_2) \) noktasından geçen ve eğimi \( f(x_2, y_2) \) olan doğrunun denklemini kullanarak \( (x_3, y_3) \) noktasının koordinatlarını bulalım.
\( f(x_2, y_2) = 5x_2y_2 = 5(\dfrac{2}{5})(\dfrac{6}{5}) = \dfrac{12}{5} \)
\( x_3 = x_2 + h = \dfrac{2}{5} + \dfrac{1}{5} = \dfrac{3}{5} \)
\( y_3 = y_2 + hf(x_2, y_2) = \dfrac{6}{5} + \dfrac{1}{5}(\dfrac{12}{5}) = \dfrac{42}{25} \)
Adım 4: \( (x_3, y_3) \) noktasından geçen ve eğimi \( f(x_3, y_3) \) olan doğrunun denklemini kullanarak \( (x_4, y_4) \) noktasının koordinatlarını bulalım.
\( f(x_3, y_3) = 5x_3y_3 = 5(\dfrac{3}{5})(\dfrac{42}{25}) = \dfrac{126}{25} \)
\( x_4 = x_3 + h = \dfrac{3}{5} + \dfrac{1}{5} = \dfrac{4}{5} \)
\( y_4 = y_3 + hf(x_3, y_3) = \dfrac{42}{25} + \dfrac{1}{5}(\dfrac{126}{25}) = \dfrac{336}{125} \)
Adım 5: \( (x_4, y_4) \) noktasından geçen ve eğimi \( f(x_4, y_4) \) olan doğrunun denklemini kullanarak \( (x_5, y_5) \) noktasının koordinatlarını bulalım.
\( f(x_4, y_4) = 5x_4y_4 = 5(\dfrac{4}{5})(\dfrac{336}{125}) = \dfrac{1344}{125} \)
\( x_5 = x_4 + h = \dfrac{4}{5} + \dfrac{1}{5} = 1 \)
\( y_5 = y_4 + hf(x_4, y_4) = \dfrac{336}{125} + \dfrac{1}{5}(\dfrac{1344}{125}) = \dfrac{3024}{625} \)
Buna göre \( y \) fonksiyonunun \( x = 1 \) noktasındaki yaklaşık değeri \( \frac{3024}{625} \) olarak bulunur.
\( y(1) \approx y_5 = \dfrac{3024}{625} \)
\( y' = 2x - 1 \)
\( y(1) = 0 \)
başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değerini aşağıdaki adım büyüklüklerini kullanarak bulunuz.
(a) herhangi bir \( h \) cinsinden
(b) \( h = \dfrac{1}{2}, \quad h = \dfrac{1}{4}, \quad h = \dfrac{1}{8} \)
(c) \( h \to 0 \) iken \( y(2) \) değerinin denklemin gerçek çözümüne yaklaştığını limit ile gösterin.
Çözümü Göster(a) seçeneği:
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 1, \quad y_0 = 0 \)
\( f(x_n, y_n) = 2x_n - 1 \)
\( x_n = x_0 + nh = 1 + nh \)
\( y_{n+1} = y_n + hf(x_n, y_n) = y_n + h(2x_n - 1) \)
Bu formülü kullanarak ilk birkaç \( n \) değeri için \( y_n \) değerlerini hesaplayalım.
| \( n = 0 \) | \( y_1 = y_0 + hf(x_0, y_0) = 0 + h(2(1) - 1) = h \) | \( = 1 \cdot h + 0 \cdot 1 \cdot h^2 \) |
| \( n = 1 \) | \( y_2 = y_1 + hf(x_1, y_1) = h + h(2(1 + h) - 1) = 2h + 2h^2 \) | \( = 2 \cdot h + 1 \cdot 2 \cdot h^2 \) |
| \( n = 2 \) | \( y_3 = y_2 + hf(x_2, y_2) = 2h + 2h^2 + h(2(1 + 2h) - 1) = 3h + 6h^2 \) | \( = 3 \cdot h + 2 \cdot 3 \cdot h^2 \) |
| \( n = 3 \) | \( y_4 = y_3 + hf(x_3, y_3) = 3h + 6h^2 + h(2(1 + 3h) - 1) = 4h + 12h^2 \) | \( = 4 \cdot h + 3 \cdot 4 \cdot h^2 \) |
İkinci sütundaki \( y_n \) değerlerini bir örüntü şeklinde üçüncü sütundaki şekilde ifade edebiliriz.
Bu örüntüyü farklı \( n \) değerleri için aşağıdaki şekilde bir formüle çevirebiliriz.
\( n \ge 1 \) olmak üzere,
\( y_n = nh + n(n - 1)h^2 \)
\( h \) adım büyüklüğü ile \( [1, 2] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{2 - 1}{h} = \dfrac{1}{h} \)
\( h = \dfrac{1}{n} \)
Denklemde yerine koyalım.
\( y_n = n(\dfrac{1}{n}) + n(n - 1)(\dfrac{1}{n})^2 = 2 - \dfrac{1}{n} \)
(b) seçeneği:
\( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değerini elde ettiğimiz eşitliği kullanarak verilen \( h \) değerleri için hesaplayalım.
\( h = \frac{1}{2} \)
\( n = \dfrac{1}{h} = \dfrac{1}{\frac{1}{2}} = 2 \)
\( y_2 = 2 - \dfrac{1}{n} = 2 - \dfrac{1}{2} = \dfrac{3}{2} \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( \frac{3}{2} \) olarak bulunur.
\( y(2) \approx y_2 = \dfrac{3}{2} \)
\( h = \frac{1}{4} \)
\( n = \dfrac{1}{h} = \dfrac{1}{\frac{1}{4}} = 4 \)
\( y_4 = 2 - \dfrac{1}{n} = 2 - \dfrac{1}{4} = \dfrac{7}{4} \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( \frac{7}{4} \) olarak bulunur.
\( y(2) \approx y_4 = \dfrac{7}{4} \)
\( h = \frac{1}{8} \)
\( n = \dfrac{1}{h} = \dfrac{1}{\frac{1}{8}} = 8 \)
\( y_8 = 2 - \dfrac{1}{n} = 2 - \dfrac{1}{8} = \dfrac{15}{8} \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( \frac{15}{8} \) olarak bulunur.
\( y(2) \approx y_8 = \dfrac{15}{8} \)
(c) seçeneği:
Denklemi düzenleyelim.
\( \dfrac{dy}{dx} = 2x - 1 \)
\( dy = (2x - 1)\ dx \)
\( x \) ve \( y \) değişkenlerine bağlı ifadeleri birbirinden ayırarak denklemi \( h(y)\ dy = f(x)\ dx \) formunda yazabildiğimiz için denklem ayrılabilir bir denklemdir.
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( \displaystyle\int {dy} = \displaystyle\int {(2x - 1)\ dx} \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y = x^2 - x + C \)
\( y(1) = 0 \) başlangıç değerini denklemde yerine koyalım.
\( 0 = 1^2 - 1 + C \)
\( C = 0 \)
Denklemin çözümü aşağıdaki gibi bulunur.
\( y = x^2 - x \)
\( y(2) = 2^2 - 2 = 2 \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki değeri \( 2 \) olarak bulunur.
\( h \to 0 \) iken \( n \to \infty \) olur.
\( \lim\limits_{n \to \infty} {y_n} = \lim\limits_{n \to \infty} \left( 2 - \dfrac{1}{n} \right) = 2 \)
\( y' = 3y - 3 \)
\( y(0) = 6 \)
başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x = 3 \) noktasındaki yaklaşık değerini aşağıdaki adım büyüklüklerini kullanarak bulunuz.
(a) herhangi bir \( h \) cinsinden
(b) \( h = \dfrac{1}{3}, \quad h = \dfrac{1}{5}, \quad h = \dfrac{1}{9} \)
(c) \( h \to 0 \) iken \( y(3) \) değerinin denklemin gerçek çözümüne yaklaştığını limit ile gösterin.
Çözümü Göster(a) seçeneği:
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 0, \quad y_0 = 6 \)
\( f(x_n, y_n) = 3y_n - 3 \)
\( x_n = x_0 + nh = nh \)
\( y_{n+1} = y_n + hf(x_n, y_n) \)
Bu formülü kullanarak ilk birkaç \( n \) değeri için \( y_n \) değerlerini hesaplayalım.
| \( n = 0 \) | \( y_1 = y_0 + hf(x_0, y_0) = 6 + h(3(6) - 3) = 6 + 15h \) | \( = 1 + 5(1 + 3h) \) |
| \( n = 1 \) | \( y_2 = y_1 + hf(x_1, y_1) = 6 + 15h + h(3(6 + 15h) - 3) = 6 + 30h + 45h^2 \) | \( = 1 + 5(1 + 3h)^2 \) |
| \( n = 2 \) | \( y_3 = y_2 + hf(x_2, y_2) = 6 + 30h + 45h^2 + h(3(6 + 30h + 45h^2) - 3) = 6 + 45h + 135h^2 + 135h^3 \) | \( = 1 + 5(1 + 3h)^3 \) |
İkinci sütundaki \( y_n \) değerlerini bir örüntü şeklinde üçüncü sütundaki şekilde ifade edebiliriz.
Bu örüntüyü farklı \( n \) değerleri için aşağıdaki şekilde bir formüle çevirebiliriz.
\( n \ge 1 \) olmak üzere,
\( y_n = 1 + 5(1 + 3h)^n \)
\( h \) adım büyüklüğü ile \( [0, 3] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{3 - 0}{h} = \dfrac{3}{h} \)
\( h = \dfrac{3}{n} \)
Denklemde yerine koyalım.
\( y_n = 1 + 5\left( 1 + \dfrac{9}{n} \right)^n \)
(b) seçeneği:
\( y \) fonksiyonunun \( x = 3 \) noktasındaki yaklaşık değerini elde ettiğimiz eşitliği kullanarak verilen \( h \) değerleri için hesaplayalım.
\( h = \frac{1}{3} \)
\( n = \dfrac{3}{h} = \dfrac{3}{\frac{1}{3}} = 9 \)
\( y_9 = 1 + 5\left( 1 + \dfrac{9}{9} \right)^9 = 1 + 5 \cdot 2^9 \)
Buna göre \( y \) fonksiyonunun \( x = 3 \) noktasındaki yaklaşık değeri \( 1 + 5 \cdot 2^9 \) olarak bulunur.
\( y(3) \approx y_9 = 1 + 5 \cdot 2^9 \)
\( h = \frac{1}{5} \)
\( n = \dfrac{3}{h} = \dfrac{3}{\frac{1}{5}} = 15 \)
\( y_{15} = 1 + 5\left( 1 + \dfrac{9}{15} \right)^{15} = 1 + 5\left( \dfrac{8}{5} \right)^{15} \)
Buna göre \( y \) fonksiyonunun \( x = 3 \) noktasındaki yaklaşık değeri \( 1 + 5\left( \dfrac{8}{5} \right)^{15} \) olarak bulunur.
\( y(3) \approx y_{15} = 1 + 5\left( \dfrac{8}{5} \right)^{15} \)
\( h = \frac{1}{9} \)
\( n = \dfrac{3}{h} = \dfrac{3}{\frac{1}{9}} = 27 \)
\( y_{27} = 1 + 5\left( 1 + \dfrac{9}{27} \right)^{27} = 1 + 5\left( \dfrac{4}{3} \right)^{27} \)
Buna göre \( y \) fonksiyonunun \( x = 3 \) noktasındaki yaklaşık değeri \( 1 + 5\left( \dfrac{4}{3} \right)^{27} \) olarak bulunur.
\( y(3) \approx y_{27} = 1 + 5\left( \dfrac{4}{3} \right)^{27} \)
(c) seçeneği:
Denklemi düzenleyelim.
\( \dfrac{dy}{dx} - 3y = -3 \)
Verilen denklem birinci mertebeden bir lineer denklemdir.
\( p(x) = -3, \quad q(x) = -3 \)
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {-3\ dx}} \)
\( = e^{-3x} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( e^{-3x}\dfrac{dy}{dx} - 3e^{-3x}y = -3e^{-3x} \)
Bu eşitliğin sol tarafı, \( \mu(x)y \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}(e^{-3x}y) = -3e^{-3x} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( e^{-3x}y + C_1 = \displaystyle\int {-3e^{-3x}\ dx} \)
\( e^{-3x}y = e^{-3x} + C \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y = 1 + Ce^{3x} \)
\( y(0) = 6 \) başlangıç değerini denklemde yerine koyalım.
\( 6 = 1 + Ce^0 \)
\( C = 5 \)
Denklemin çözümü aşağıdaki gibi bulunur.
\( y = 1 + 5e^{3x} \)
\( y(3) = 1 + 5e^9 \)
Buna göre \( y \) fonksiyonunun \( x = 3 \) noktasındaki değeri \( 3 \) olarak bulunur.
\( h \to 0 \) iken \( n \to \infty \) olur.
\( \lim\limits_{n \to \infty} {y_n} = \lim\limits_{n \to \infty} \left( 1 + 5\left( 1 + \dfrac{9}{n} \right)^n \right) = 1 + 5e^9 \)
\( y' = y - 2x \)
\( y(0) = 1 \)
başlangıç değer probleminin çözümü olan \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değerini aşağıdaki adım büyüklüklerini kullanarak bulunuz.
(a) herhangi bir \( h \) cinsinden
(b) \( h = \dfrac{1}{2}, \quad h = \dfrac{1}{4}, \quad h = \dfrac{1}{8} \)
(c) \( h \to 0 \) iken \( y(2) \) değerinin denklemin gerçek çözümüne yaklaştığını limit ile gösterin.
Çözümü Göster(a) seçeneği:
Başlangıç noktası aşağıdaki şekilde veriliyor.
\( x_0 = 0, \quad y_0 = 1 \)
\( f(x_n, y_n) = y_n - 2x_n \)
\( x_n = x_0 + nh = nh \)
\( y_{n+1} = y_n + hf(x_n, y_n) \)
Bu formülü kullanarak ilk birkaç \( n \) değeri için \( y_n \) değerlerini hesaplayalım.
| \( n = 0 \) | \( y_1 = y_0 + hf(x_0, y_0) = 1 + h(1 - 2(0)) = 1 + h \) | \( = 2 + 1 \cdot 2 \cdot h - (1 + h)^1 \) |
| \( n = 1 \) | \( y_2 = y_1 + hf(x_1, y_1) = 1 + h + h((1 + h) - 2(h)) = 1 + 2h - h^2 \) | \( = 2 + 2 \cdot 2 \cdot h - (1 + h)^2 \) |
| \( n = 2 \) | \( y_3 = y_2 + hf(x_2, y_2) = 1 + 2h - h^2 + h((1 + 2h - h^2) - 2(2h)) = 1 + 3h - 3h^2 - h^3 \) | \( = 2 + 3 \cdot 2 \cdot h - (1 + h)^3 \) |
İkinci sütundaki \( y_n \) değerlerini bir örüntü şeklinde üçüncü sütundaki şekilde ifade edebiliriz.
Bu örüntüyü farklı \( n \) değerleri için aşağıdaki şekilde bir formüle çevirebiliriz.
\( n \ge 1 \) olmak üzere,
\( y_n = 2 + 2nh - (1 + h)^n \)
\( h \) adım büyüklüğü ile \( [0, 2] \) aralığında gerekli olan adım sayısını bulalım.
\( n = \dfrac{2 - 0}{h} = \dfrac{2}{h} \)
\( h = \dfrac{2}{n} \)
Denklemde yerine koyalım.
\( y_n = 2 + 2n(\dfrac{2}{n}) - \left( 1 + \dfrac{2}{n} \right)^n = 6 - \left( 1 + \dfrac{2}{n} \right)^n \)
(b) seçeneği:
\( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değerini elde ettiğimiz eşitliği kullanarak verilen \( h \) değerleri için hesaplayalım.
\( h = \frac{1}{2} \)
\( n = \dfrac{2}{h} = \dfrac{2}{\frac{1}{2}} = 4 \)
\( y_4 = 6 - \left( 1 + \dfrac{2}{4} \right)^4 = 6 - \left( \dfrac{3}{2} \right)^4 \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( 6 - \left( \dfrac{3}{2} \right)^4 \) olarak bulunur.
\( y(2) \approx y_4 = 6 - \left( \dfrac{3}{2} \right)^4 \)
\( h = \frac{1}{4} \)
\( n = \dfrac{2}{h} = \dfrac{2}{\frac{1}{4}} = 8 \)
\( y_8 = 6 - \left( 1 + \dfrac{2}{8} \right)^8 = 6 - \left( \dfrac{5}{4} \right)^8 \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki yaklaşık değeri \( 6 - \left( \dfrac{5}{4} \right)^8 \) olarak bulunur.
\( y(2) \approx y_8 = 6 - \left( \dfrac{5}{4} \right)^8 \)
\( h = \frac{1}{8} \)
\( n = \dfrac{2}{h} = \dfrac{2}{\frac{1}{8}} = 16 \)
\( y_{16} = 6 - \left( 1 + \dfrac{2}{16} \right)^{16} = 6 - \left( \dfrac{9}{8} \right)^{16} \)
Buna göre \( y \) fonksiyonunun \( x = 3 \) noktasındaki yaklaşık değeri \( 6 - \left( \dfrac{9}{8} \right)^{16} \) olarak bulunur.
\( y(2) \approx y_{16} = 6 - \left( \dfrac{9}{8} \right)^{16} \)
(c) seçeneği:
Denklemi düzenleyelim.
\( \dfrac{dy}{dx} - y = -2x \)
Verilen denklem birinci mertebeden bir lineer denklemdir.
\( p(x) = -1, \quad q(x) = -2x \)
Denklemin integral çarpanını bulalım.
\( \mu(x) = e^{\int {-1\ dx}} \)
\( = e^{-x} \)
Denklemin taraflarını integral çarpanı ile çarpalım.
\( e^{-x}\dfrac{dy}{dx} - e^{-x}y = -2xe^{-x} \)
Bu eşitliğin sol tarafı, \( \mu(x)y \) çarpımının türevinin çarpma kuralı ile açılımına eşittir.
\( \dfrac{d}{dx}(e^{-x}y) = -2xe^{-x} \)
Eşitliğin taraflarının ayrı ayrı integralini alalım.
\( e^{-x}y + C_1 = \displaystyle\int {-2xe^{-x}\ dx} \)
Eşitliğin sağ tarafındaki ifadenin integralini almak için kısmi integral alma yöntemini kullanalım.
\( u \) ve \( dv \) ifadelerini aşağıdaki gibi belirleyelim.
\( u = -2x \)
\( dv = e^{-x}\ dx \)
Buna göre \( du \) ve \( v \) aşağıdaki gibi olur.
\( du = -2dx \)
\( v = -e^{-x} \)
Bu ifadeleri \( \int {u\ dv} = uv - \int {v\ du} \) kısmi integral formülünde yerine koyalım.
\( = 2xe^{-x} - \displaystyle\int {2e^{-x}\ dx} \)
\( e^{-x}y = 2xe^{-x} + 2e^{-x} + C \)
Denklemin genel çözümü aşağıdaki gibi bulunur.
\( y = 2x + 2 + Ce^x \)
\( y(0) = 1 \) başlangıç değerini denklemde yerine koyalım.
\( 1 = 2(0) + 2 + Ce^0 \)
\( C = -1 \)
Denklemin çözümü aşağıdaki gibi bulunur.
\( y = 2x + 2 - e^x \)
\( y(2) = 6 - e^2 \)
Buna göre \( y \) fonksiyonunun \( x = 2 \) noktasındaki değeri \( 6 - e^2 \) olarak bulunur.
\( h \to 0 \) iken \( n \to \infty \) olur.
\( \lim\limits_{n \to \infty} {y_n} = \lim\limits_{n \to \infty} \left( 6 - \left( 1 + \dfrac{2}{n} \right)^n \right) = 6 - e^2 \)