Laplace Dönüşümünün Varlığı
Bir fonksiyonun Laplace dönüşümü, tanımındaki genelleştirilmiş integralin bir reel sayı olarak tanımlı olduğu (yani yakınsak olduğu) \( s \) değerlerinde tanımlıdır, aksi (yani integralin ıraksak olduğu) durumda ise tanımsızdır.
\( \mathcal{L}\{ f(t) \} = \displaystyle\int_{0}^{\infty} {e^{-st}f(t)\ dt} \)
Bu tanımdaki integralin yakınsak, dolayısıyla Laplace dönüşümünün tanımlı olmasını sağlayan iki koşul, fonksiyonun parçalı sürekli olması ve \( \alpha \) mertebeden üstel olmasıdır.
Parçalı Sürekli Fonksiyon
Süreksiz olduğu noktalar sonlu sayıda olan ve bu noktalarda sadece sıçrama süreksizliği içeren fonksiyonlara parçalı sürekli fonksiyon denir.
Parçalı sürekli fonksiyonların bazı özellikleri aşağıdaki gibidir.
- Süreksiz oldukları sonlu sayıda noktada sonsuz ya da salınım süreksizliği içermezler.
- Süreksiz oldukları noktalar arasındaki açık aralıklarda süreklidirler.
- Sıçrama süreksizliğinin bir özelliği olarak, süreksiz oldukları noktalarda soldan ve sağdan limitleri birer reel sayı olarak tanımlıdır, ancak birbirinden farklıdır.
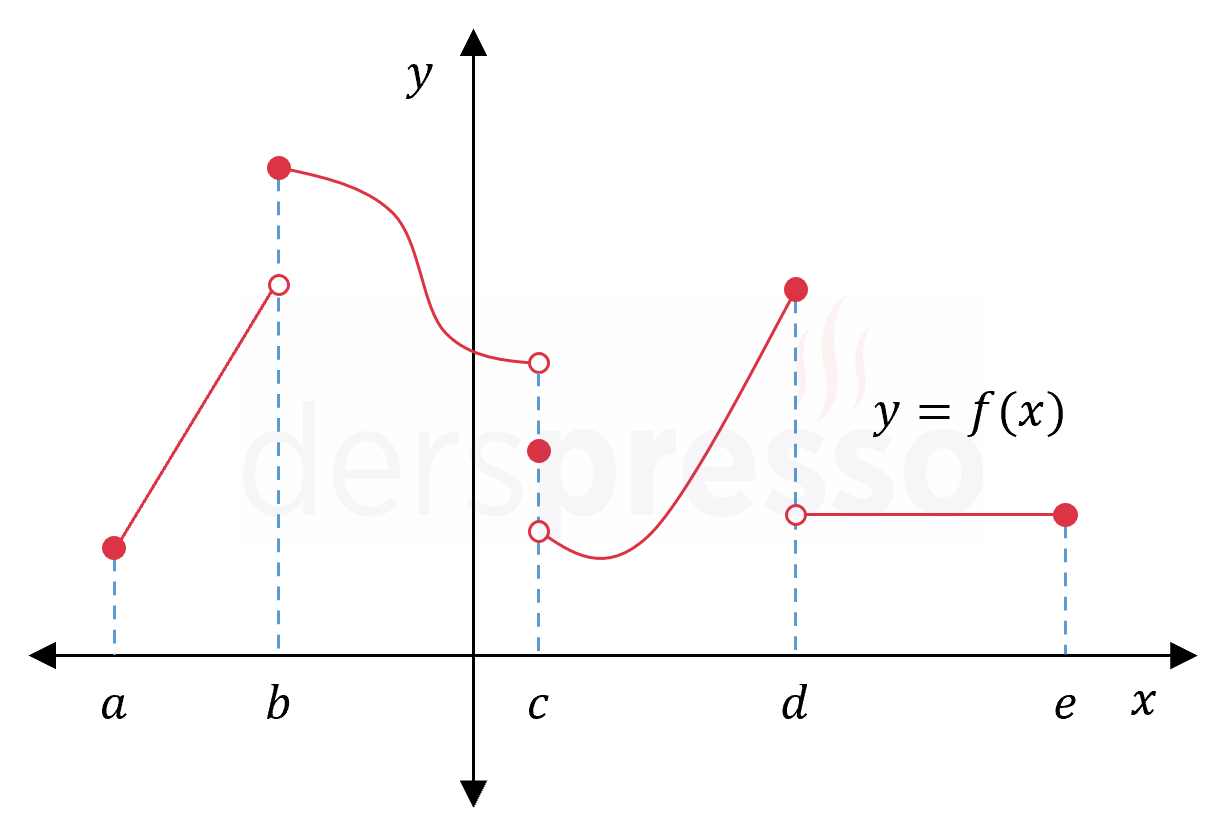
Aşağıda grafiği verilen \( f \) fonksiyonu, sıçrama süreksizliğine sahip olduğu sonlu sayıda nokta dışında sürekli olduğu için parçalı sürekli bir fonksiyondur.
\( \alpha \) Mertebeden Üstel Fonksiyon
\( \alpha \) mertebeden üstel fonksiyon aşağıdaki şekilde tanımlanır.
\( M, T \in \mathbb{R^+} \) olmak üzere,
\( f \) fonksiyonunun tanımlı olduğu her \( t \gt T \) için,
\( \abs{f(t)} \lt Me^{\alpha t} \) eşitsizliğini sağlayan birer \( M \) ve \( T \) varsa,
\( f \) fonksiyonu \( \alpha \) mertebeden üstel bir fonksiyondur.
Bu eşitsizliğin taraflarını \( e^{-st} \) ile çarpalım.
\( e^{-st}\abs{f(t)} \lt Me^{-(s - \alpha)t} \)
\( e^{-st}\abs{f(t)} \lt \dfrac{M}{e^{(s - \alpha)t}} \)
Buna göre, \( f \) fonksiyonu \( \alpha \) mertebeden üstel bir fonksiyon ise \( s \gt \alpha \) olduğu durumda \( e^{-st} \) fonksiyonunun küçülme hızı \( f(t) \) fonksiyonunun büyüme hızını geçer, bunun bir sonucu olarak \( e^{-st}f(t) \) çarpımı \( t \) sonsuza giderken sıfıra gider ve Laplace dönüşümü tanımındaki integral yakınsak olur.
\( f \) fonksiyonu \( \alpha \) mertebeden üstel bir fonksiyon ise,
\( \lim\limits_{t \to \infty} {e^{-st}f(t)} = 0 \)
Bir diğer ifadeyle, \( f \) fonksiyonu \( \alpha \) mertebeden üstel bir fonksiyon ise \( \abs{f(t)} \) fonksiyonu \( t \gt T \) için bir üstel fonksiyonun (\( e^{\alpha t} \)) \( M \) katına ait fonksiyonun grafiği ile üstten sınırlıdır.
Tüm sınırlı fonksiyonlar \( \alpha = 0 \) mertebeden üsteldir, dolayısıyla \( s \gt 0 \) için Laplace dönüşümleri tanımlıdır. Buna göre sinüs ve kosinüs fonksiyonları ve sabit fonksiyonlar \( \alpha = 0 \) mertebeden üsteldir.
\( f(t) \) bir sınırlı fonksiyon olmak üzere,
\( \abs{f(t)} \lt Me^{0t} = M \)
\( f(t) = \sin(3t) \)
\( \abs{\sin(3t)} \lt 2 \)
\( e^{at} \) formundaki üstel fonksiyonlar \( \alpha = a \) mertebeden üsteldir, dolayısıyla \( s \gt a \) için Laplace dönüşümleri tanımlıdır.
\( f(t) \) bir üstel fonksiyon olmak üzere,
\( \abs{f(t)} \lt Me^{at} \)
\( f(t) = e^{5t} \)
\( \abs{e^{5t}} \lt 2e^{5t} \)
Laplace Dönüşümünün Varlığı
Yukarıdaki iki tanım ışığında, bir fonksiyon \( [0, \infty) \) aralığında parçalı sürekli ve \( \alpha \) mertebeden üstel ise fonksiyonun \( s \gt \alpha \) aralığında Laplace dönüşümü tanımlıdır.
İntegrali ıraksak olan, dolayısıyla Laplace dönüşümü tanımlı olmayan fonksiyonlara aşağıdaki iki örnek verilebilir.
\( f(t) = \dfrac{1}{t} \)
\( g(t) = e^{t^2} \)