Fonksiyon Grafikleri
Fonksiyonların birinci ve ikinci türevi, fonksiyonların grafikleri ve davranışları hakkında bize önemli bilgiler verir. Bu bölümde önce fonksiyon grafikleri ile ilgili bazı önemli kavramları inceleyeceğiz, daha sonra bu kavramları ve türev fonksiyonlarını kullanarak grafiklerle ilgili daha detaylı yorumlar yapmaya çalışacağız.
Sabit, Artan ve Azalan Aralıklar
Bir fonksiyonun değerinin belirli bir aralıkta sabit kalması, sürekli artması ya da sürekli azalmasına göre fonksiyonun bu aralıkta sabit, artan ya da azalan bir fonksiyon olduğunu söyleriz.
Sabit Aralık
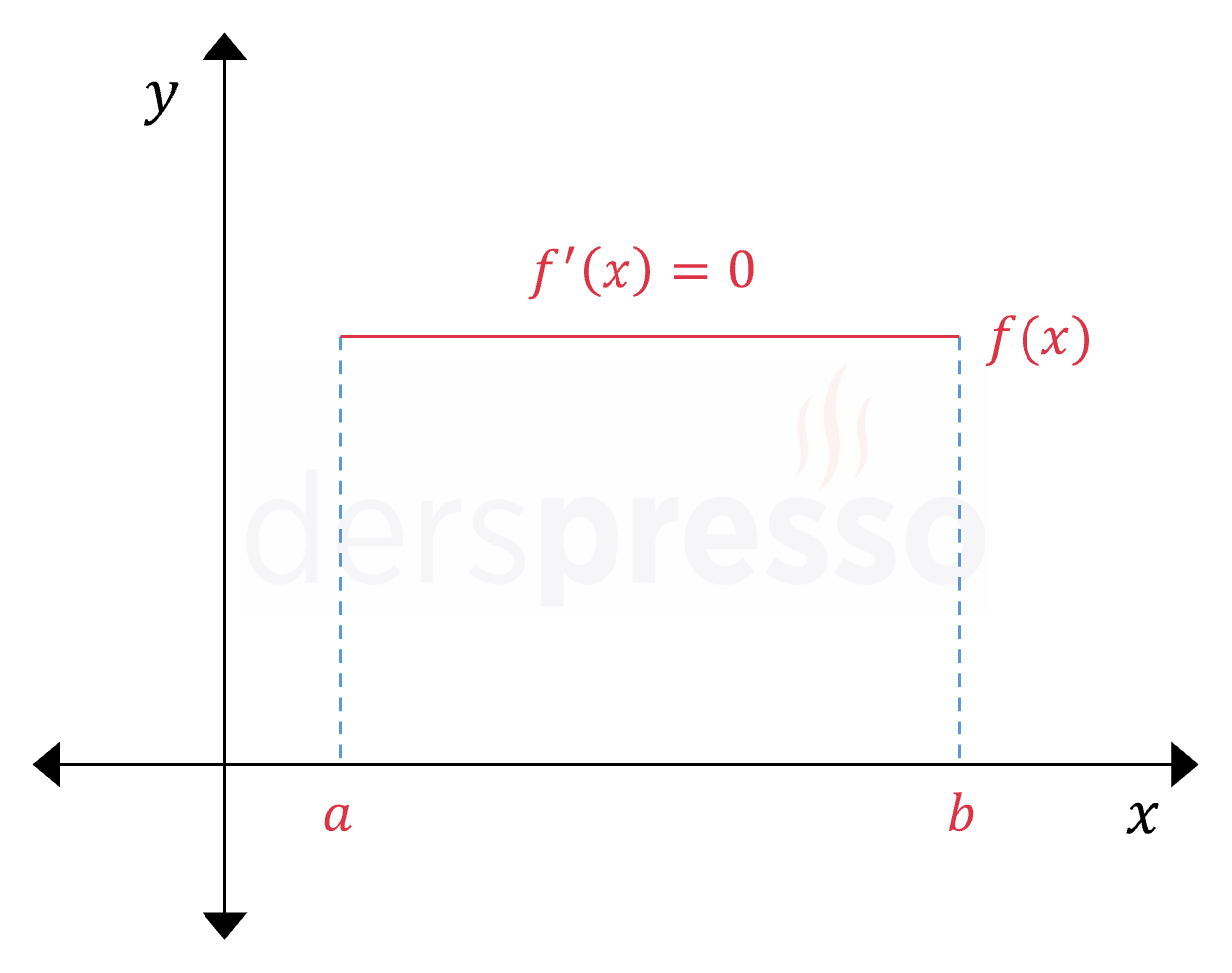
Aşağıda \( (a, b) \) aralığında sabit bir fonksiyonun grafiği verilmiştir. Bir fonksiyonun değerinin sabit kaldığı bir aralıkta eğimi sıfır olduğu için, bu aralıkta birinci türevi de sıfırdır.
Artan Aralık
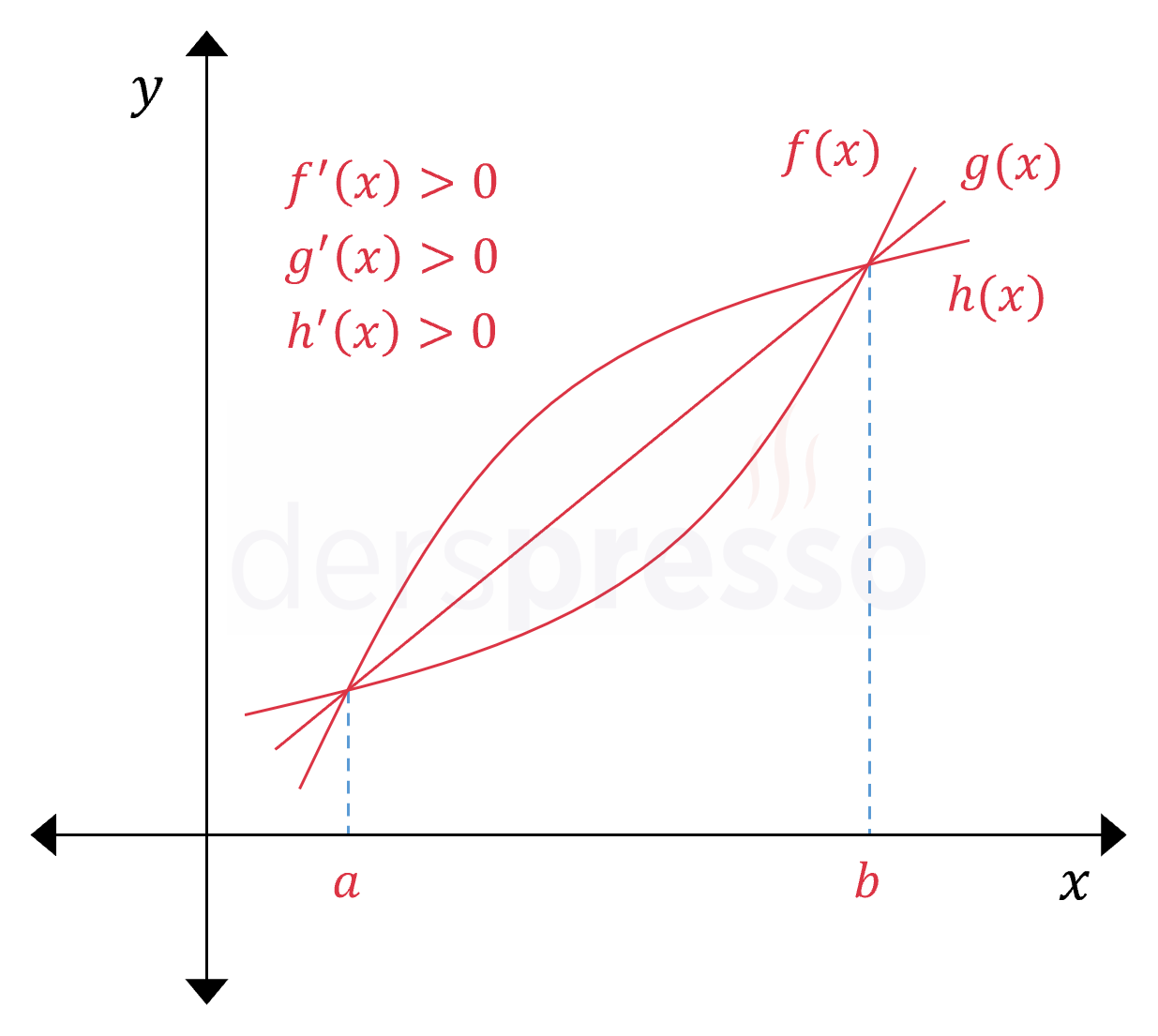
Aşağıda \( (a, b) \) aralığında farklı şekillerde artan üç fonksiyonun grafiği verilmiştir. Bir fonksiyonun değerinin sürekli arttığı bir aralıkta eğimi pozitif olduğu için, bu aralıkta bu üç fonksiyonun da birinci türevi pozitiftir.
Azalan Aralık
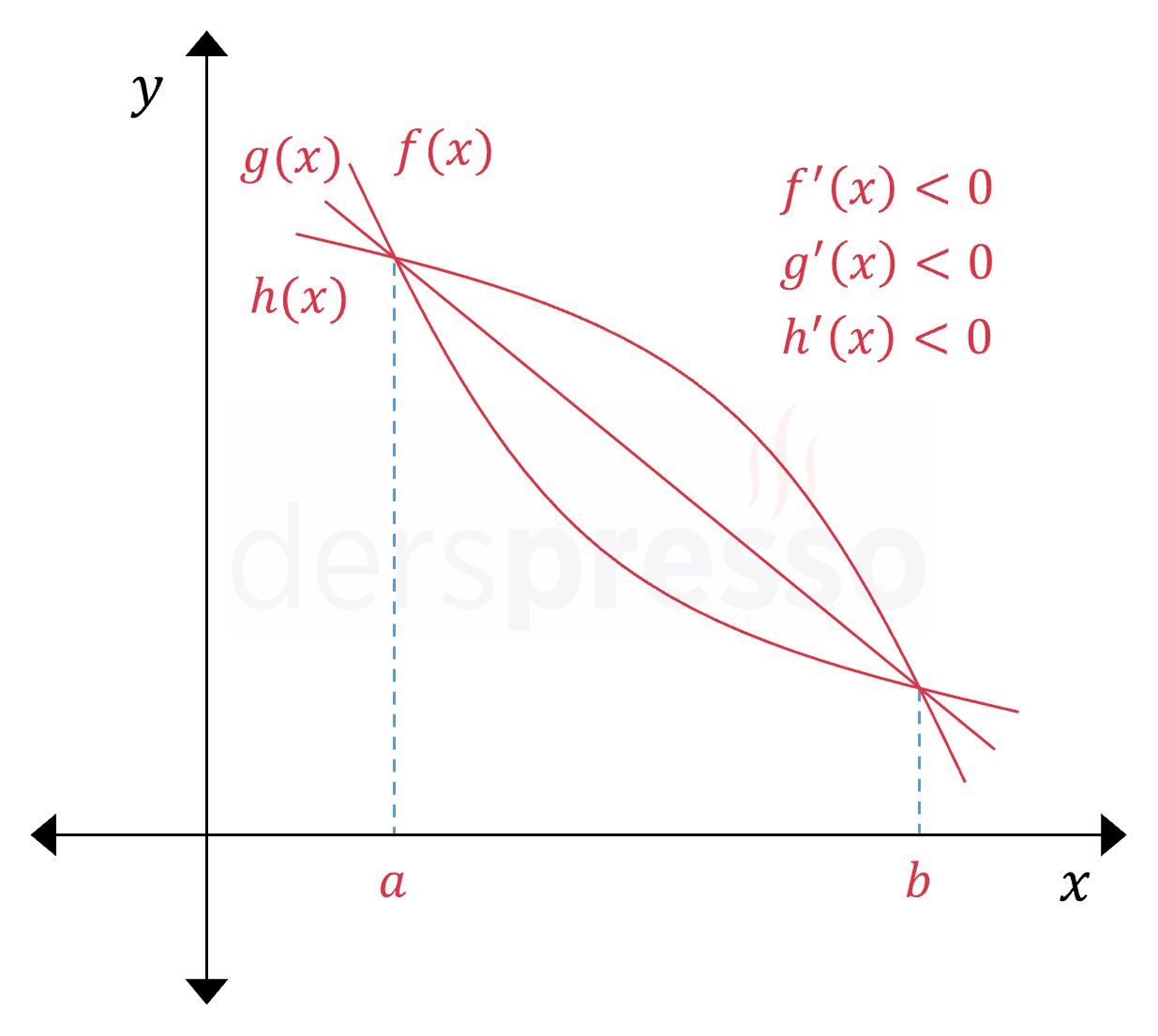
Aşağıda \( (a, b) \) aralığında farklı şekillerde azalan üç fonksiyonun grafiği verilmiştir. Bir fonksiyonun değerinin sürekli azaldığı bir aralıkta eğimi negatif olduğu için, bu aralıkta bu üç fonksiyonun da birinci türevi negatiftir.
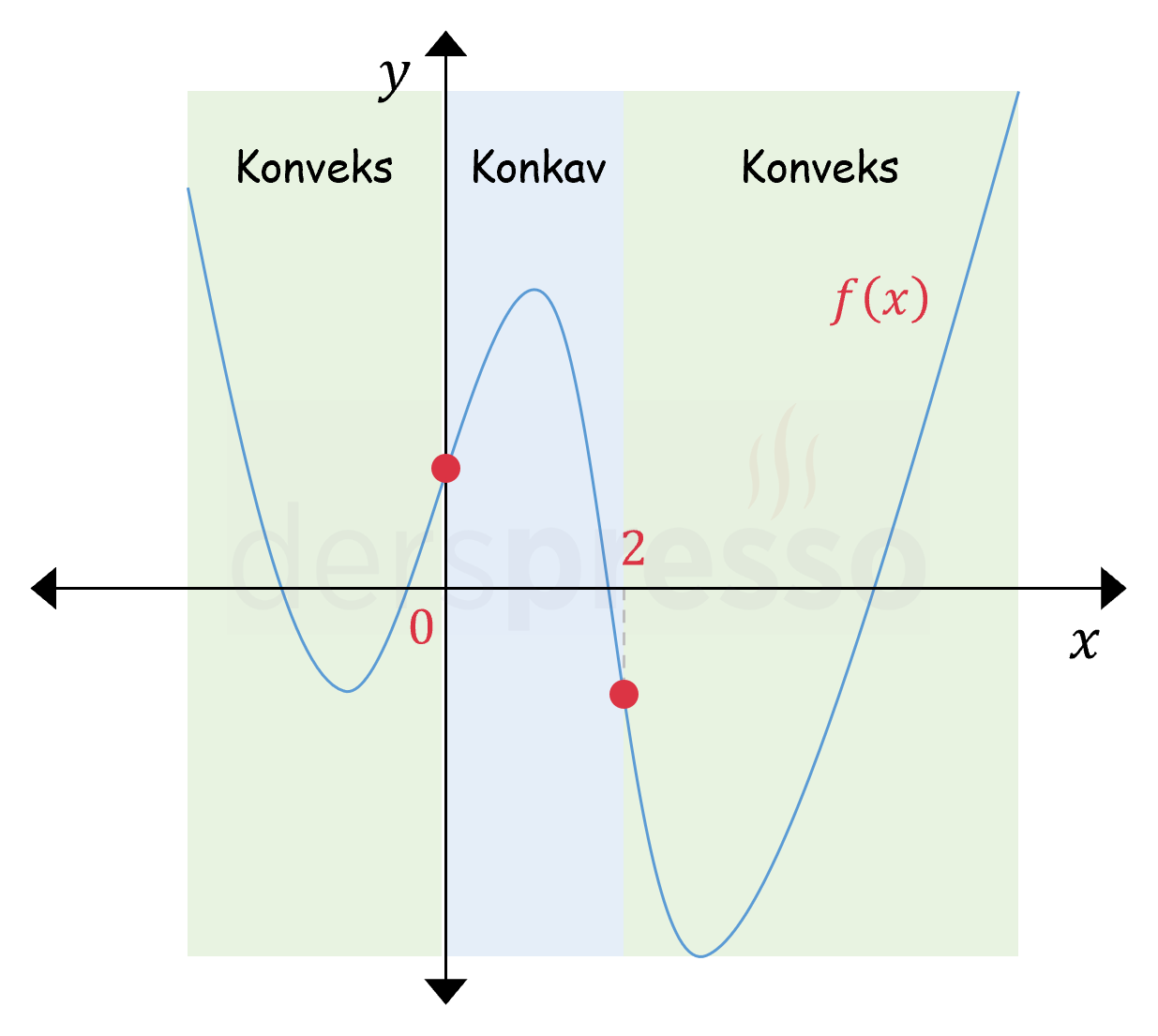
Konveks ve Konkav Aralıklar
Konveks (Dış Bükey) Aralık
Bir fonksiyonun bir aralıktaki grafiği bu aralığın uç noktalarını birleştiren doğrunun altında kalıyorsa fonksiyon grafiği bu aralıkta konvekstir (dış bükeydir).
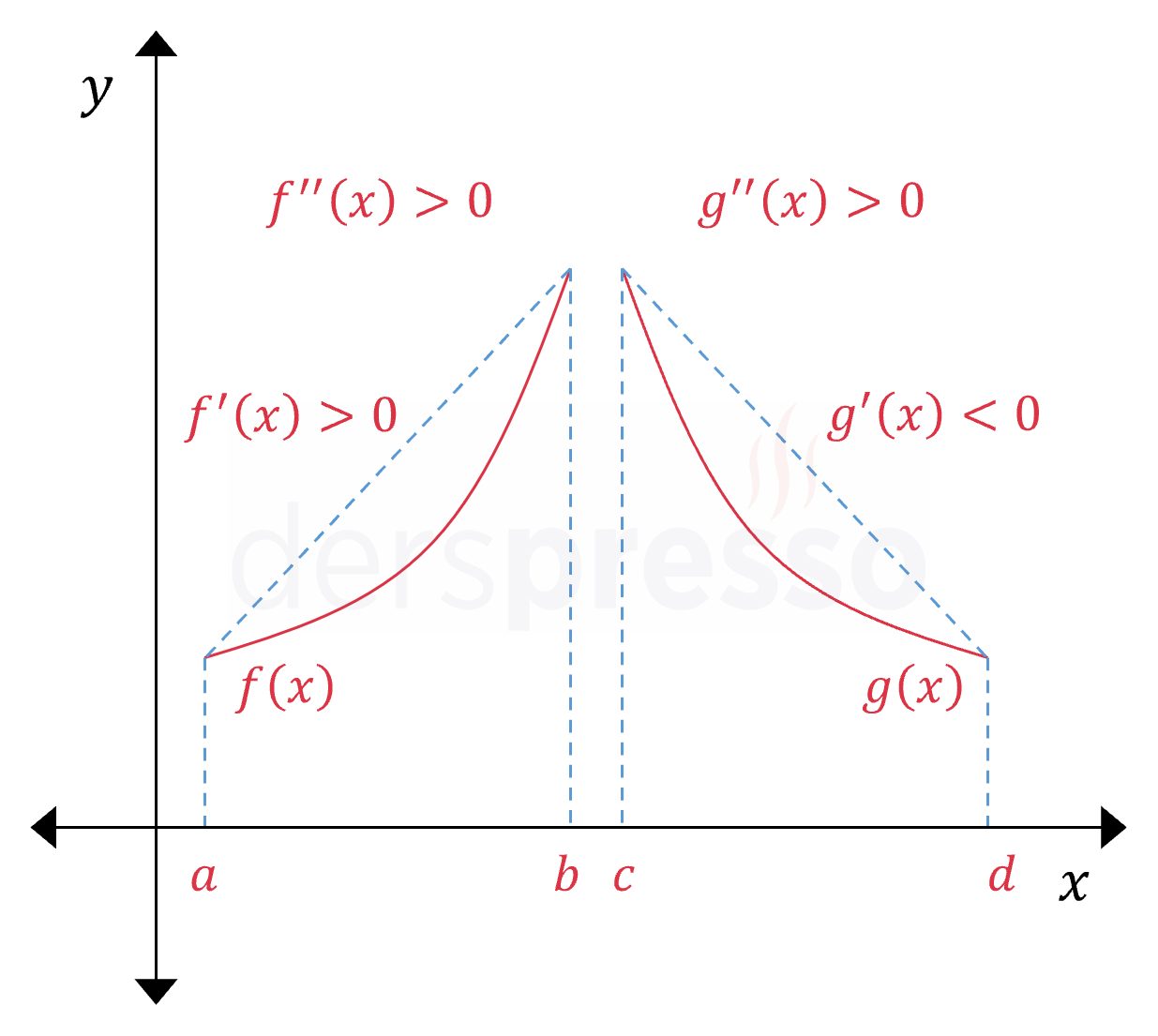
Konveks bir grafik şekildeki \( f \) fonksiyonu gibi artan (pozitif eğim ve birinci türev) ya da \( g \) fonksiyonu gibi azalan (negatif eğim ve birinci türev) olabilir, ancak eğim değeri (birinci türevi) her zaman artandır, dolayısıyla ikinci türevi pozitiftir.
Konkav (İç Bükey) Aralık
Bir fonksiyonun bir aralıktaki grafiği bu aralığın uç noktalarını birleştiren doğrunun üstünde kalıyorsa fonksiyon grafiği bu aralıkta konkavdır (iç bükeydir).

Konkav bir grafik şekildeki \( f \) fonksiyonu gibi artan (pozitif eğim ve birinci türev) ya da \( g \) fonksiyonu gibi azalan (negatif eğim ve birinci türev) olabilir, ancak eğim değeri (birinci türevi) her zaman azalandır, dolayısıyla ikinci türevi negatiftir.
Örnek Aralıklar ve Türevleri
Yukarıda bahsettiğimiz aralık tipleri için fonksiyonların birinci ve ikinci türevlerinin grafiklerinin nasıl oluştuğu aşağıda bazı örnekler üzerinden gösterilmiştir.
| Grafik | Açıklama |
|---|---|

|
Sabit Aralık Ana fonksiyonun değeri sabittir. Ana fonksiyonun eğimi sıfır olduğu için birinci türev de sabit ve sıfırdır (\( f'(x) = 0 \)). Birinci türevin eğimi sabit olduğu için ikinci türev sıfırdır (\( f''(x) = 0 \)). |
|
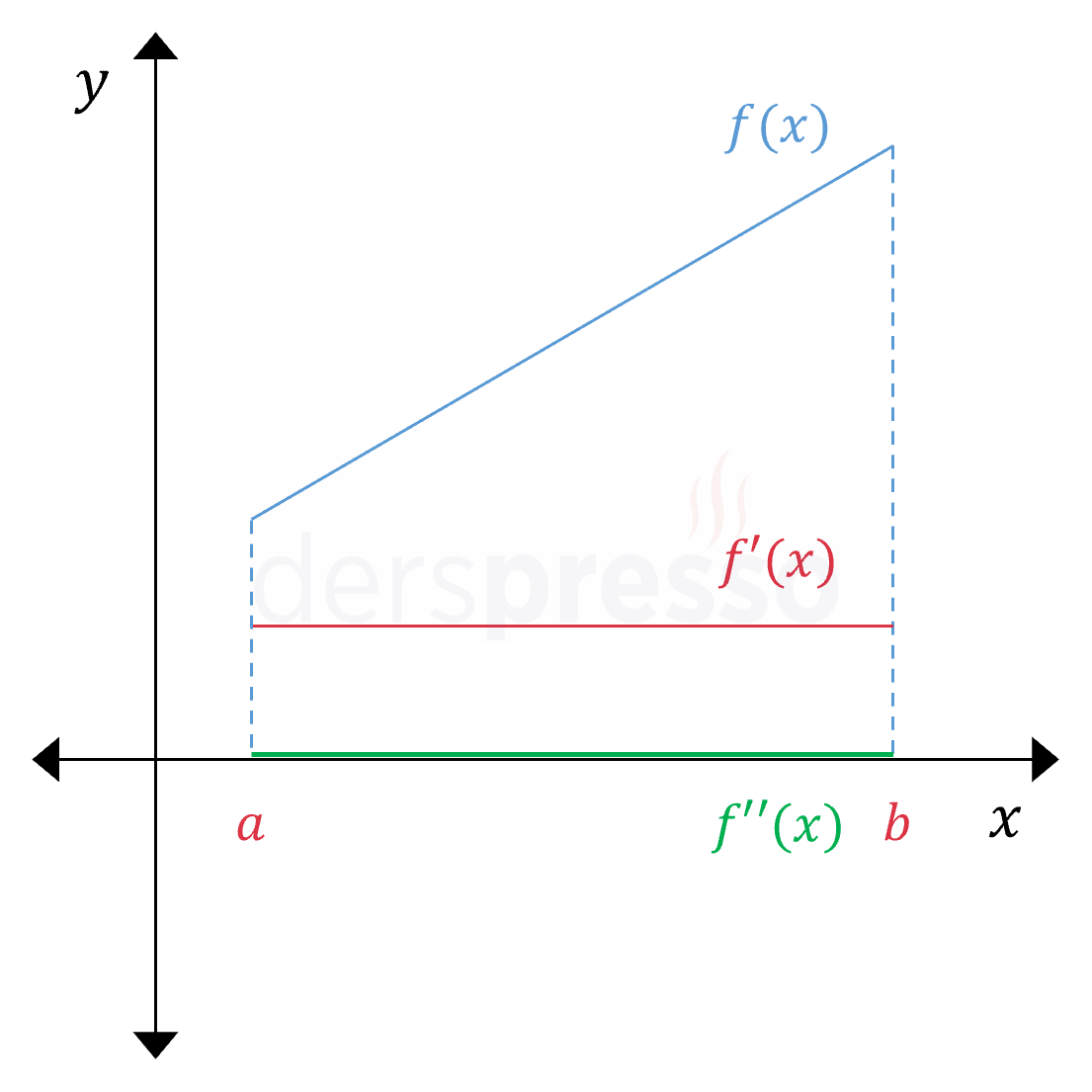
Sabit Oranda Artan Aralık Ana fonksiyonun değeri doğrusal bir şekilde artar. Ana fonksiyonun eğimi pozitif ve sabit olduğu için birinci türev de pozitif ve sabittir. Birinci türevin eğimi sabit olduğu için ikinci türev sıfırdır (\( f''(x) = 0 \)). |
|
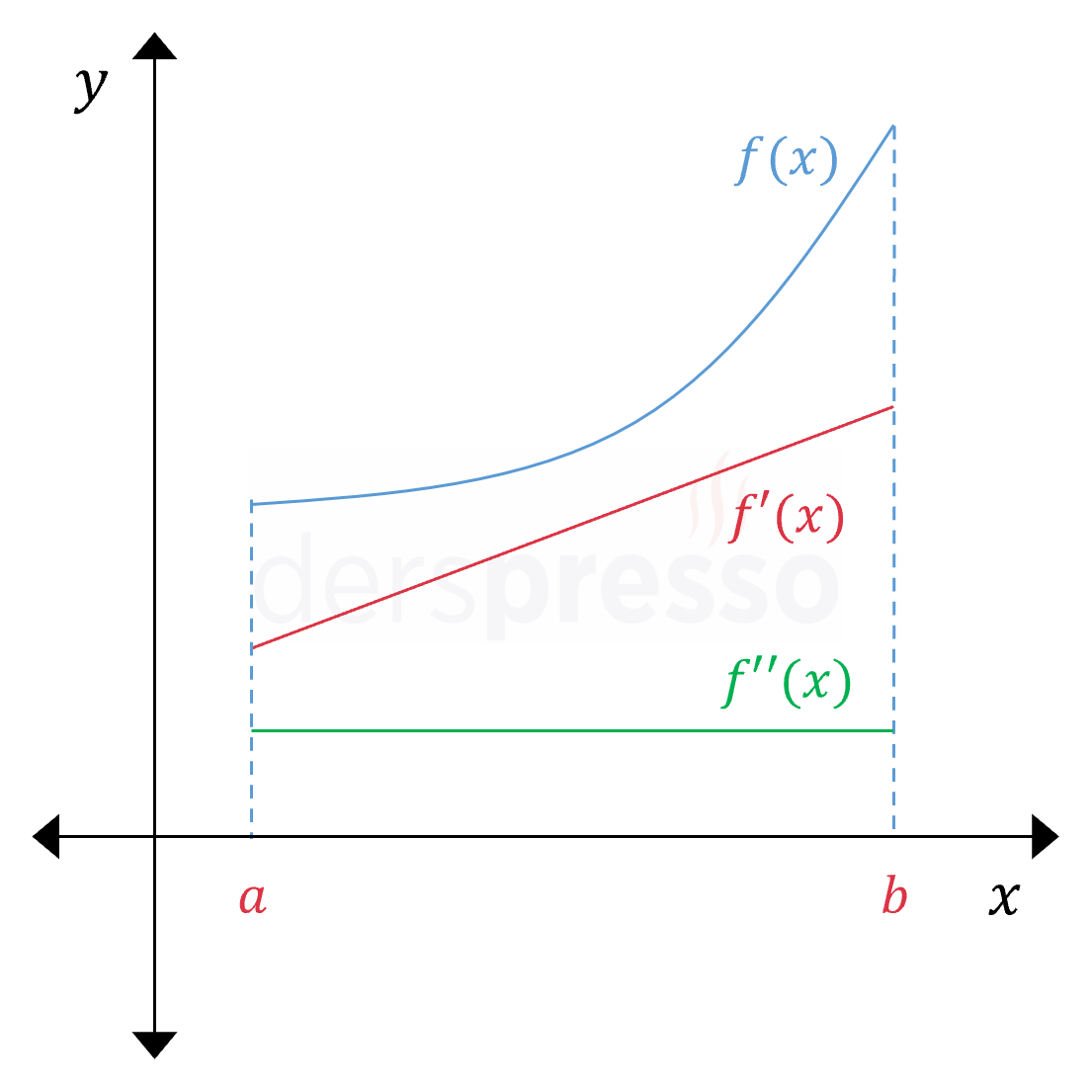
Konveks (Artış Hızı Artarak) Artan Aralık Ana fonksiyonun değeri artış hızı artarak artar. Ana fonksiyonun eğimi pozitiftir ve artmaktadır, dolayısıyla birinci türev de pozitif ve artandır. Birinci türev artan olduğu için ikinci türev pozitiftir (\( f''(x) \gt 0 \)). NOT: Ana fonksiyonun denklemine göre birinci türevin grafiği pozitif ve artan olmak koşuluyla doğrusal ya da eğrisel olabilir. Buna bağlı olarak ikinci türevin grafiği pozitif tarafta kalmak koşuluyla artan ya da azalan, doğrusal ya da eğrisel olabilir. |
|
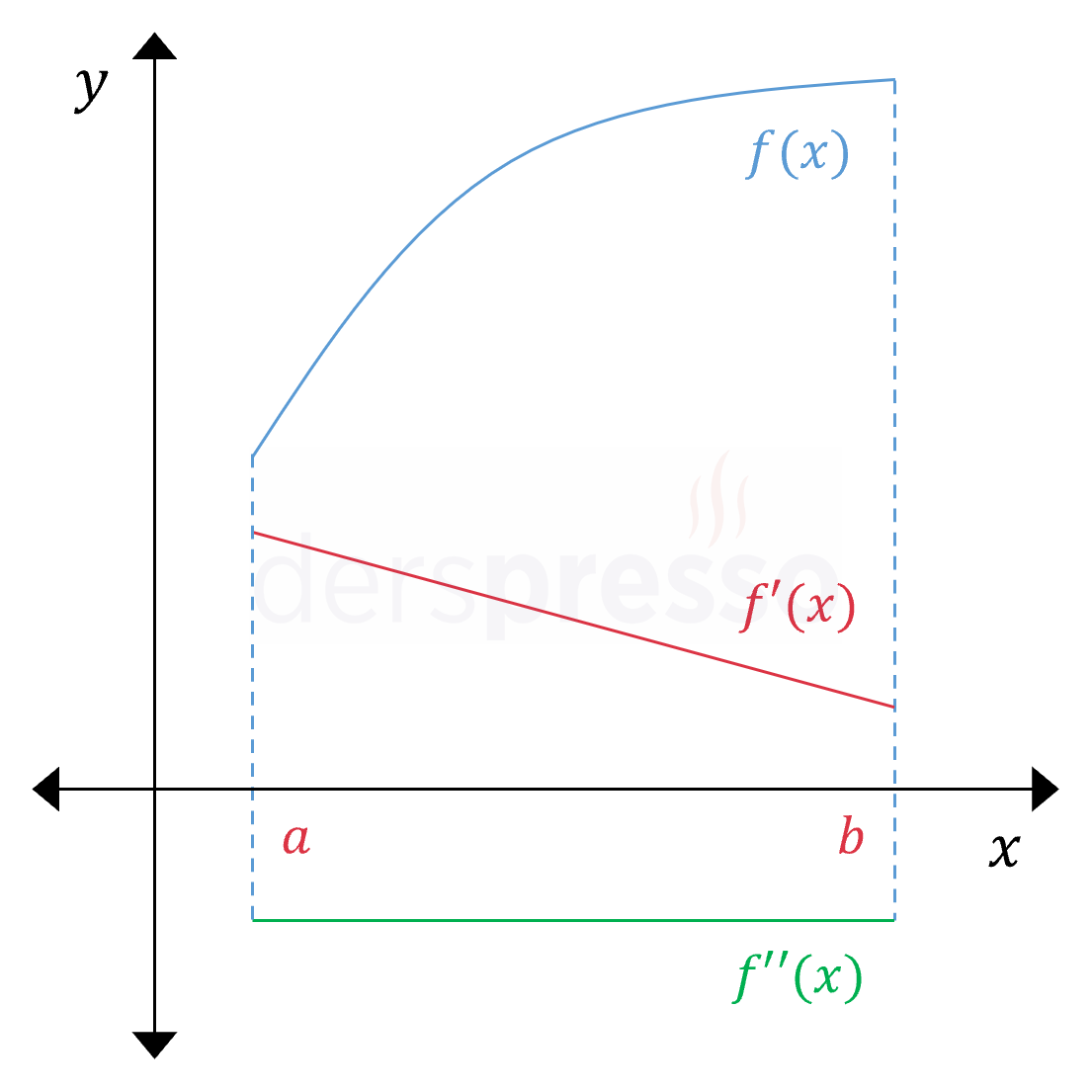
Konkav (Artış Hızı Azalarak) Artan Aralık Ana fonksiyonun değeri artış hızı azalarak artar. Ana fonksiyonun eğimi pozitiftir ve azalmaktadır, dolayısıyla birinci türev de pozitif ve azalandır. Birinci türev azalan olduğu için ikinci türev negatiftir (\( f''(x) \lt 0 \)). Yukarıda verdiğimiz not bu grafiğe de uyarlanabilir. |
|
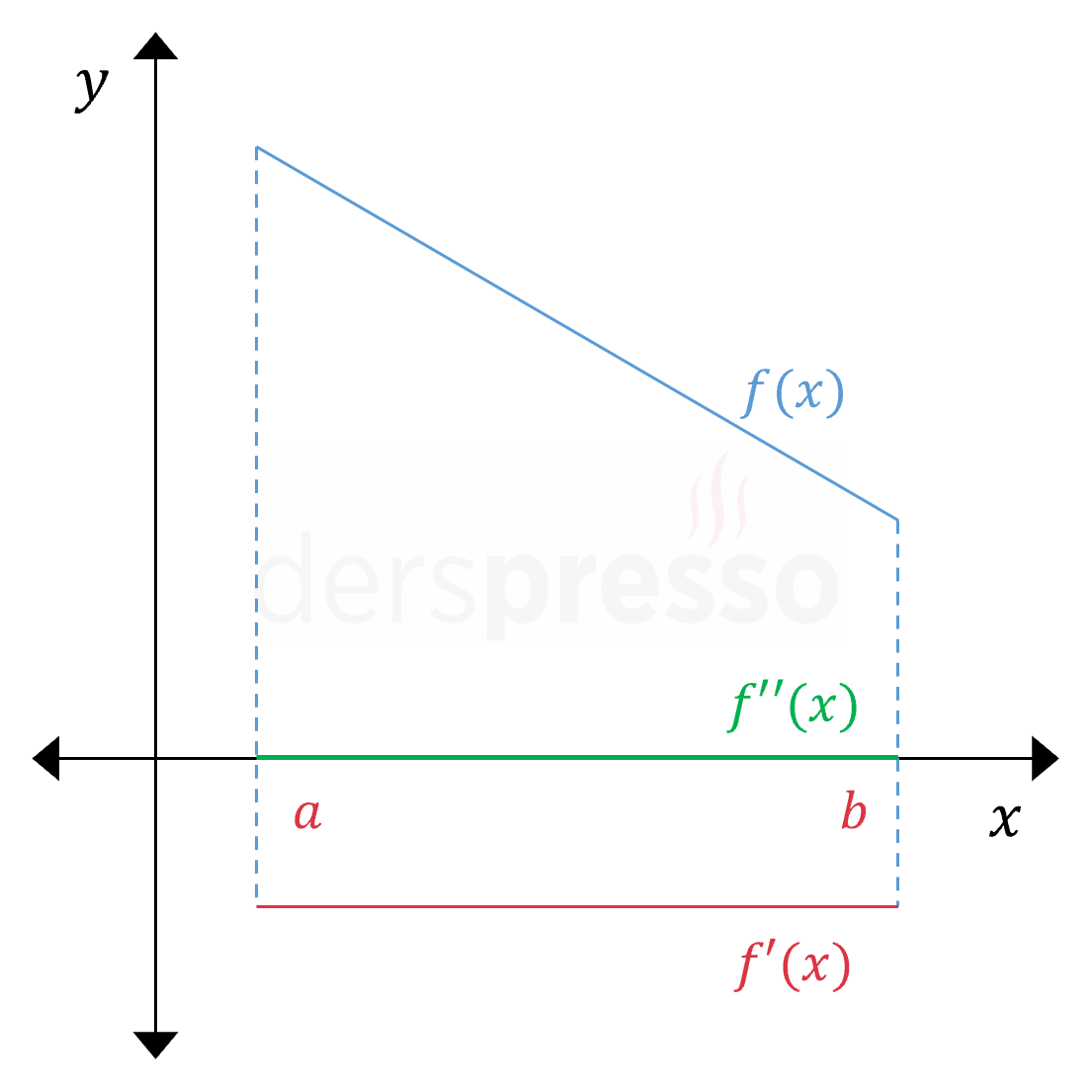
Sabit Oranda Azalan Aralık Ana fonksiyonun değeri doğrusal bir şekilde azalır. Ana fonksiyonun eğimi negatif ve sabit olduğu için birinci türev de negatif ve sabittir. Birinci türevin eğimi sabit olduğu için ikinci türev sıfırdır (\( f''(x) = 0 \)). |
|
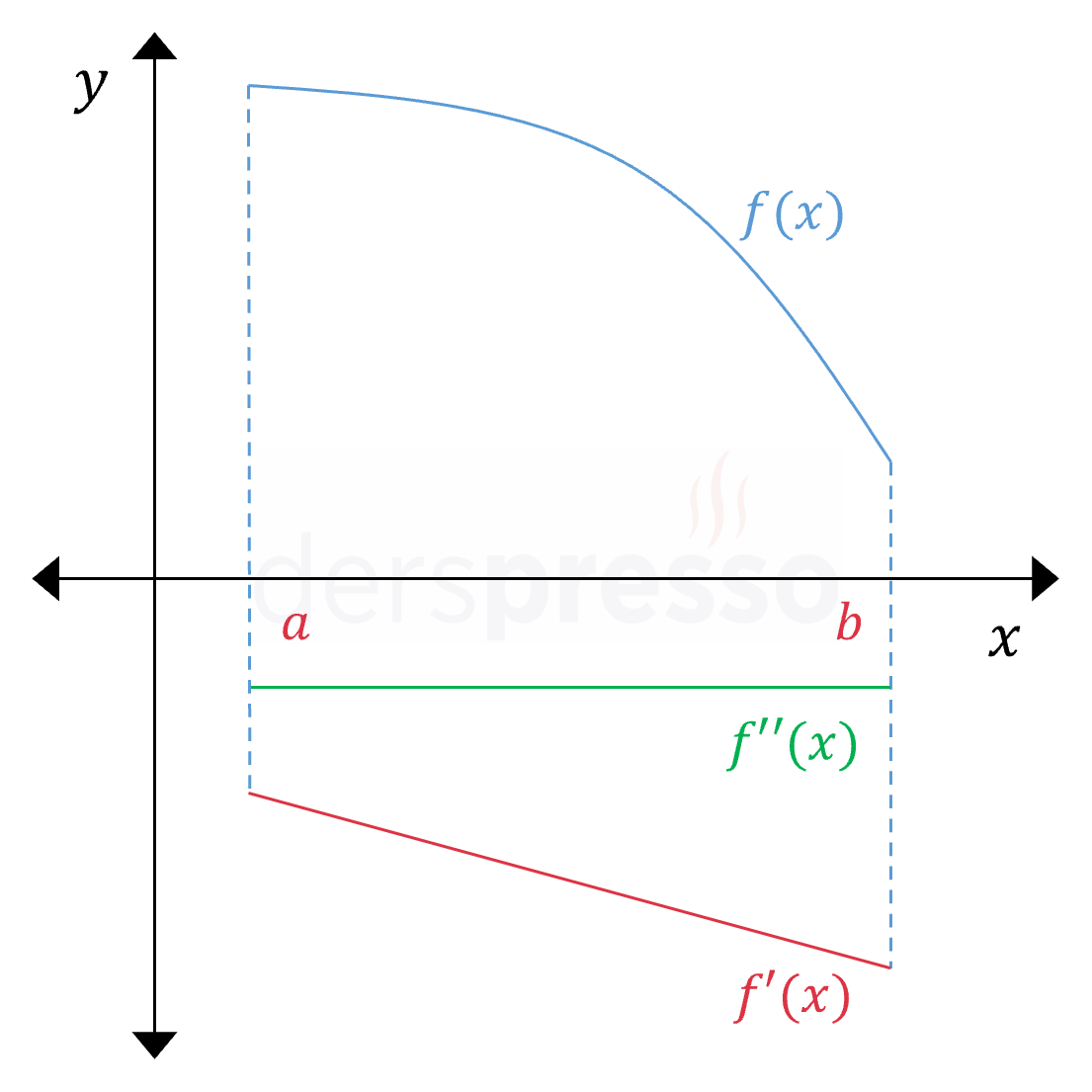
Konkav (Azalış Hızı Artarak) Azalan Aralık Ana fonksiyonun değeri azalış hızı mutlak değer olarak artarak azalır. Ana fonksiyonun eğimi negatiftir ve azalmaktadır, dolayısıyla birinci türev de negatif ve azalandır. Birinci türev azalan olduğu için ikinci türev negatiftir (\( f''(x) \lt 0 \)). Yukarıda verdiğimiz not bu grafiğe de uyarlanabilir. |
|
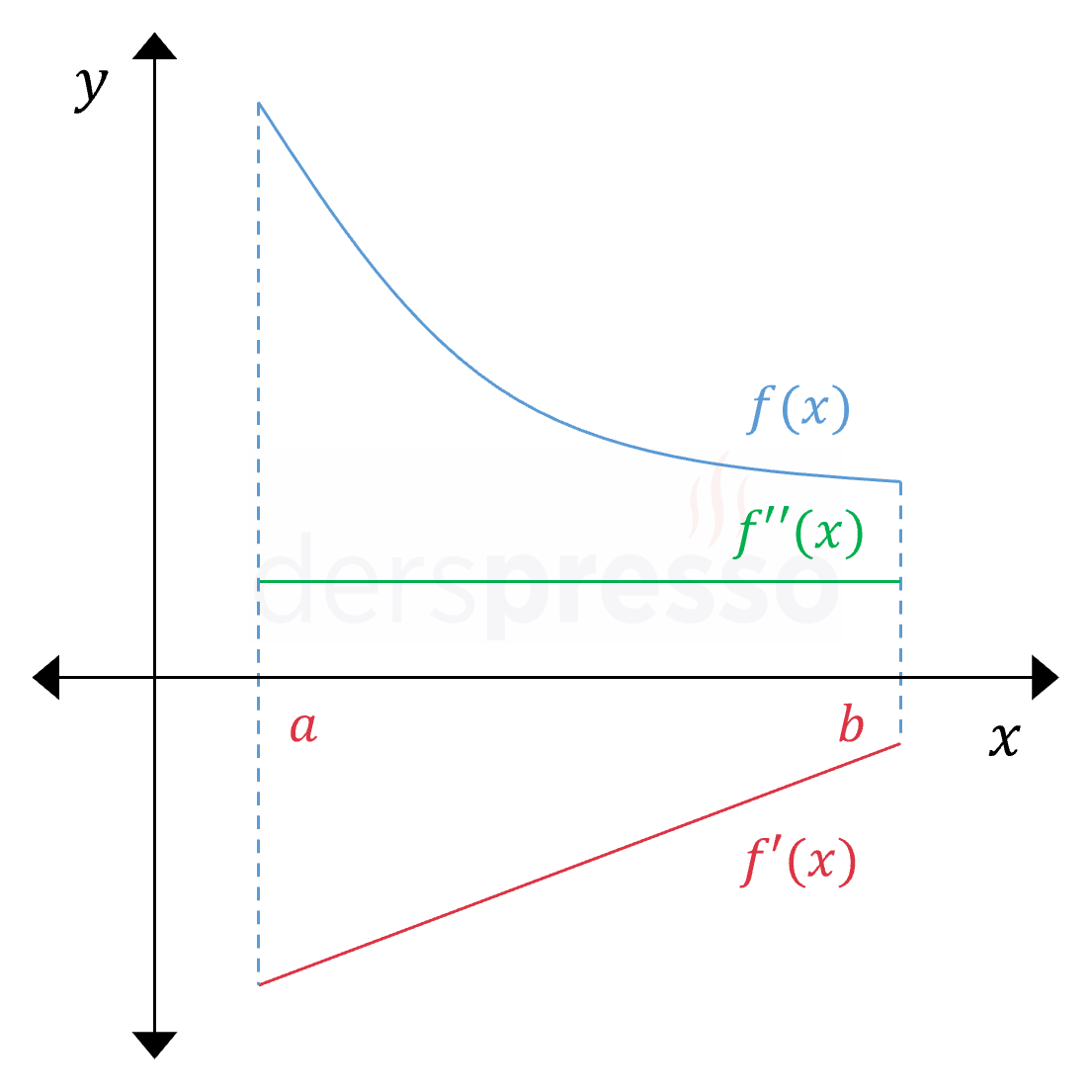
Konveks (Azalış Hızı Azalarak) Azalan Aralık Ana fonksiyonun değeri azalış hızı mutlak değer olarak azalarak azalır. Ana fonksiyonun eğimi negatiftir ve artmaktadır, dolayısıyla birinci türev de negatif ve artandır. Birinci türev artan olduğu için ikinci türev pozitiftir (\( f''(x) \gt 0 \)). Yukarıda verdiğimiz not bu grafiğe de uyarlanabilir. |
|
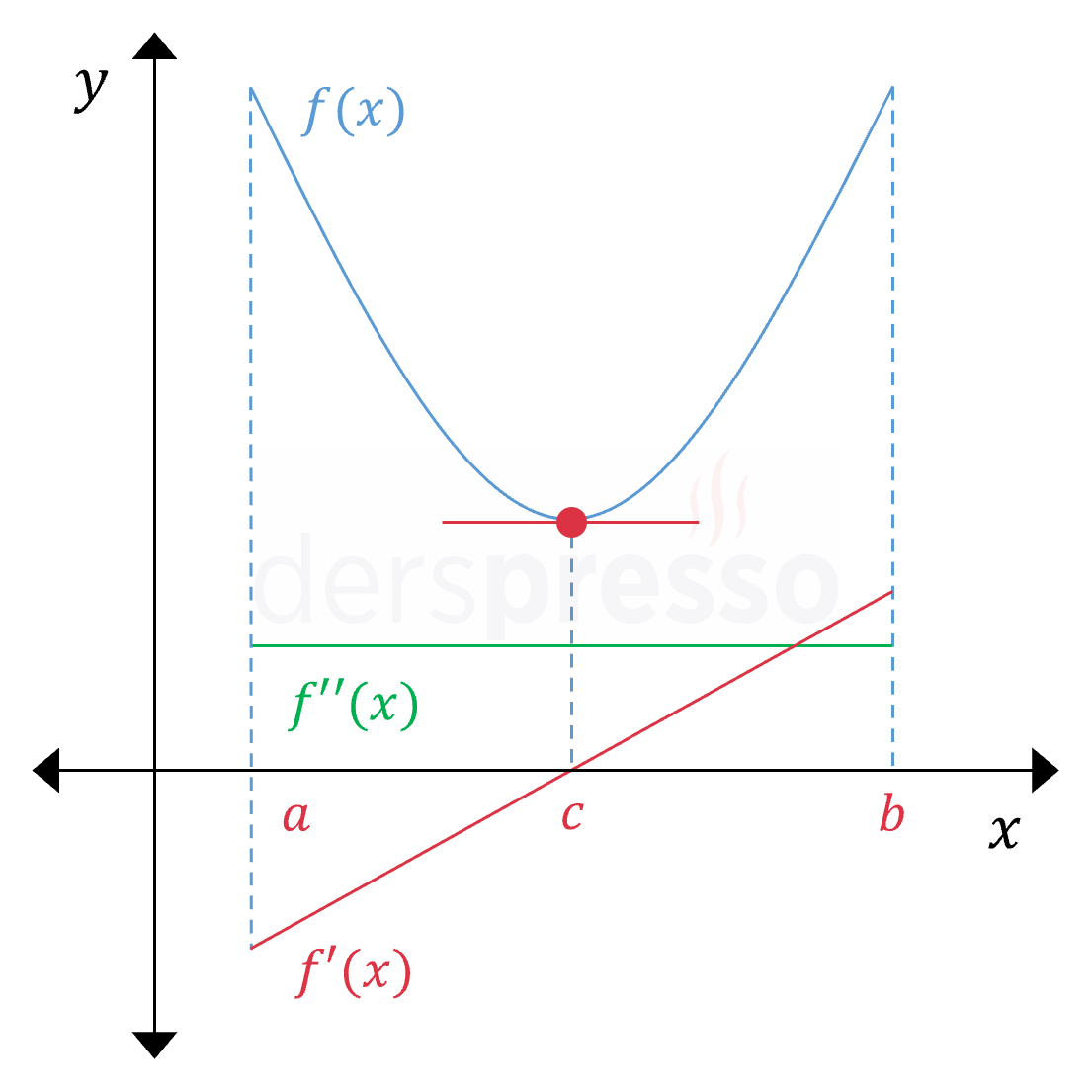
Önce Azalan Sonra Artan Aralık Ana fonksiyonun değeri \( (a, c) \) aralığında azalış hızı mutlak değer olarak azalarak azalır, \( (c, b) \) aralığında ise artış hızı artarak artar. Ana fonksiyonun eğimi \( (a, c) \) aralığında negatif, \( c \) noktasında sıfır, \( (c, b) \) aralığında pozitiftir ve tüm aralıkta artandır. Birinci türev tüm aralıkta artan olduğu için ikinci türev pozitiftir (\( f''(x) \gt 0 \)). Yukarıda verdiğimiz not bu grafiğe de uyarlanabilir. |
|
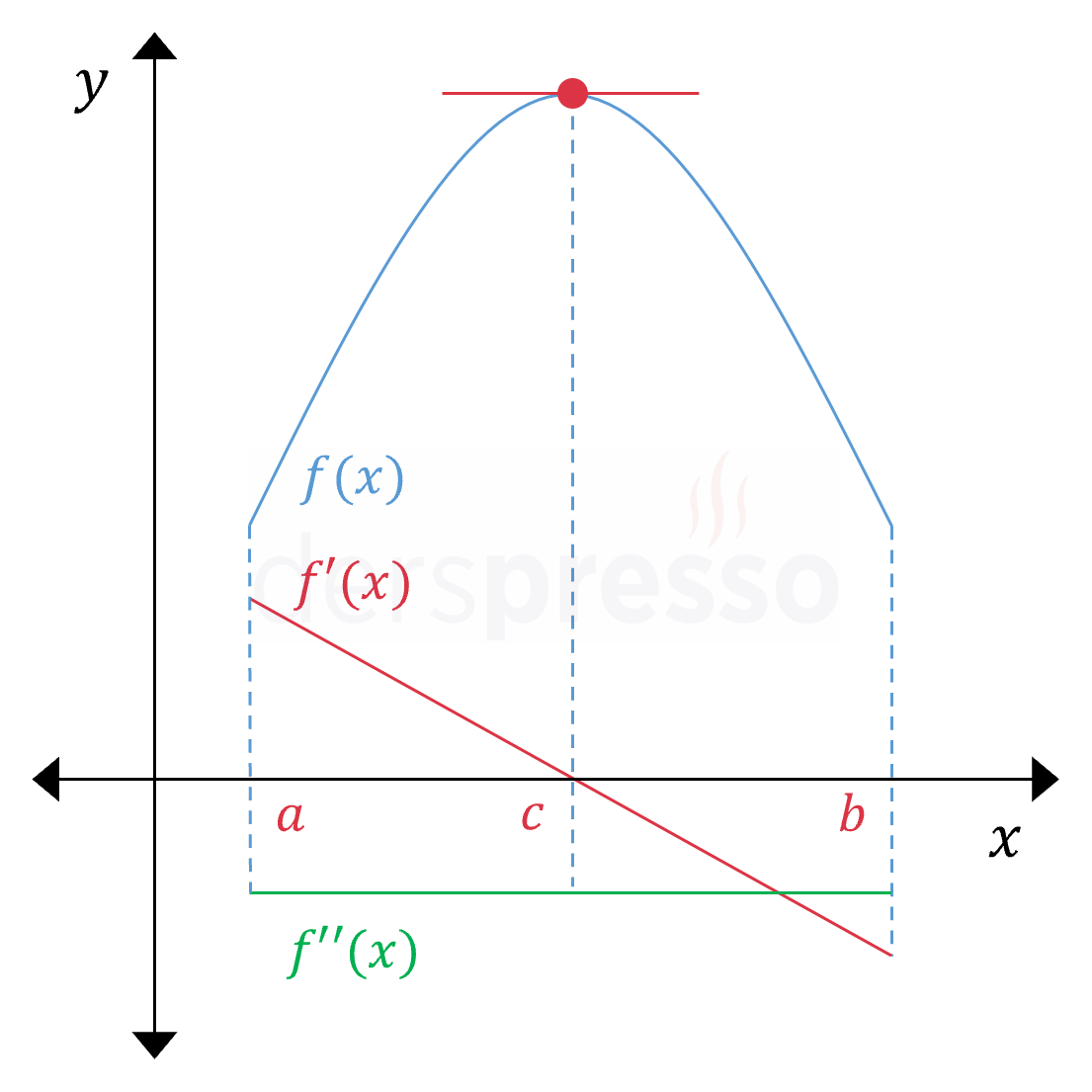
Önce Artan Sonra Azalan Aralık Ana fonksiyonun değeri \( (a, c) \) aralığında artış hızı azalarak artar, \( (c, b) \) aralığında ise azalış hızı mutlak değer olarak artarak azalır. Ana fonksiyonun eğimi \( (a, c) \) aralığında pozitif, \( c \) noktasında sıfır, \( (c, b) \) aralığında negatiftir ve tüm aralıkta azalandır. Birinci türev tüm aralıkta azalan olduğu için ikinci türev negatiftir (\( f''(x) \lt 0 \)). Yukarıda verdiğimiz not bu grafiğe de uyarlanabilir. |
\( f(x) = x^4 - 4x^3 + 6x + 1 \) fonksiyonunun konveks ve konkav olduğu aralıklar nedir?
Çözümü Göster