Büküm Noktalarının Bulunması
Aşağıdaki tabloda önceki bölümlerde gördüğümüz durağan noktaların, türevlenebilir ekstremum noktaların ve büküm noktalarının bir özeti verilmiştir.

Bir büküm noktası fonksiyonun birinci türevinin (eğiminin) artarken azalmaya ya da azalırken artmaya başladığı nokta olduğu için, bu noktada fonksiyonun birinci türevi aynı zamanda türevlenebilir bir yerel minimum ya da maksimum noktası olur.
Buna göre bir noktanın büküm noktası olup olmadığını anlamak için ana fonksiyonun yerel minimum/maksimum noktalarını bulmak için kullandığımız yöntemi fonksiyonun birinci türevine uygulayabiliriz.
Aşağıdaki iki koşul sağlanıyorsa \( x = a \) noktası \( f \) fonksiyonunun bir büküm noktasıdır.
(1) İkinci türev bu noktada sıfır olmalıdır (\( f''(a) = 0 \)).
(2) İkinci türev bu noktada işaret değiştirmelidir.
Bir fonksiyonun belirli bir noktada ikinci türevinin işaret değiştirip değiştirmediğini yerel minimum/maksimum noktalarını bulmak için kullandığımız iki yöntemle kontrol edebiliriz.
Birinci yöntemde ikinci türevin bu noktanın solundaki ve sağındaki işaretleri karşılaştırılır.
İkinci yöntemde ise fonksiyonun bu noktadaki üçüncü türevine bakılır.
\( x = a \) noktası \( f \) fonksiyonunun birinci türevinin bir durağan noktası olmak üzere (\( f''(a) = 0 \)),
\( f'''(a) \ne 0 \) ise bu nokta bir büküm noktasıdır.
Yukarıdaki koşulları sağlayan bir büküm noktasının yatay (durağan) bir büküm noktası olması için, ek olarak fonksiyonun birinci türevi sıfıra eşit olmalıdır. Bu koşul sağlanmıyorsa bu büküm noktası durağan olmayan bir büküm noktasıdır.
Bir büküm noktasının yatay (durağan) bir büküm noktası olması için ek koşul:
\( f'(x) = 0 \)
\( f(x) = \frac{1}{2}x^4 - 3x^2+ 4x + 2 \) fonksiyonunun büküm noktalarının apsis değerlerini ve her büküm noktasının tipini bulalım.
Büküm noktaları ikinci türevin işaret değiştirdiği noktalarda oluşur.
\( f'(x) = 2x^3 - 6x + 4 \)
\( f''(x) = 6x^2 - 6 \)
İkinci türevin köklerini bulalım.
\( f''(x) = 6x^2 - 6 = 0 \)
\( f''(x) = 6(x + 1)(x - 1) = 0 \)
\( x \in \{-1, 1\} \)
İkinci türevin bu noktalarda işaret değiştirip değiştirmediğini bir işaret tablosu ile bulalım.
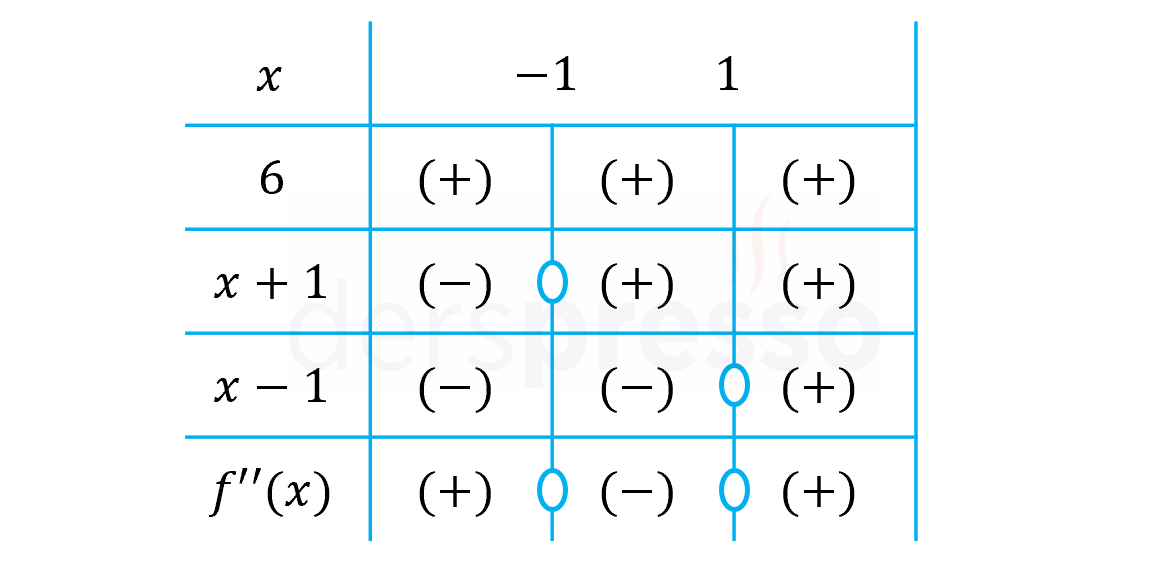
İkinci türev hem \( x = -1 \) hem de \( x = 1 \) noktasında sıfır olduğu ve işaret değiştirdiği için iki nokta da birer büküm noktasıdır.
Bu noktaların hangi tipte büküm noktaları olduğunu bulmak için apsis değerlerini birinci türevde yerine koyalım.
\( f'(-1) = 2(-1)^3 - 6(-1) + 4 = 8 \)
\( f'(1) = 2(1)^3 - 6(1) + 4 = 0 \)
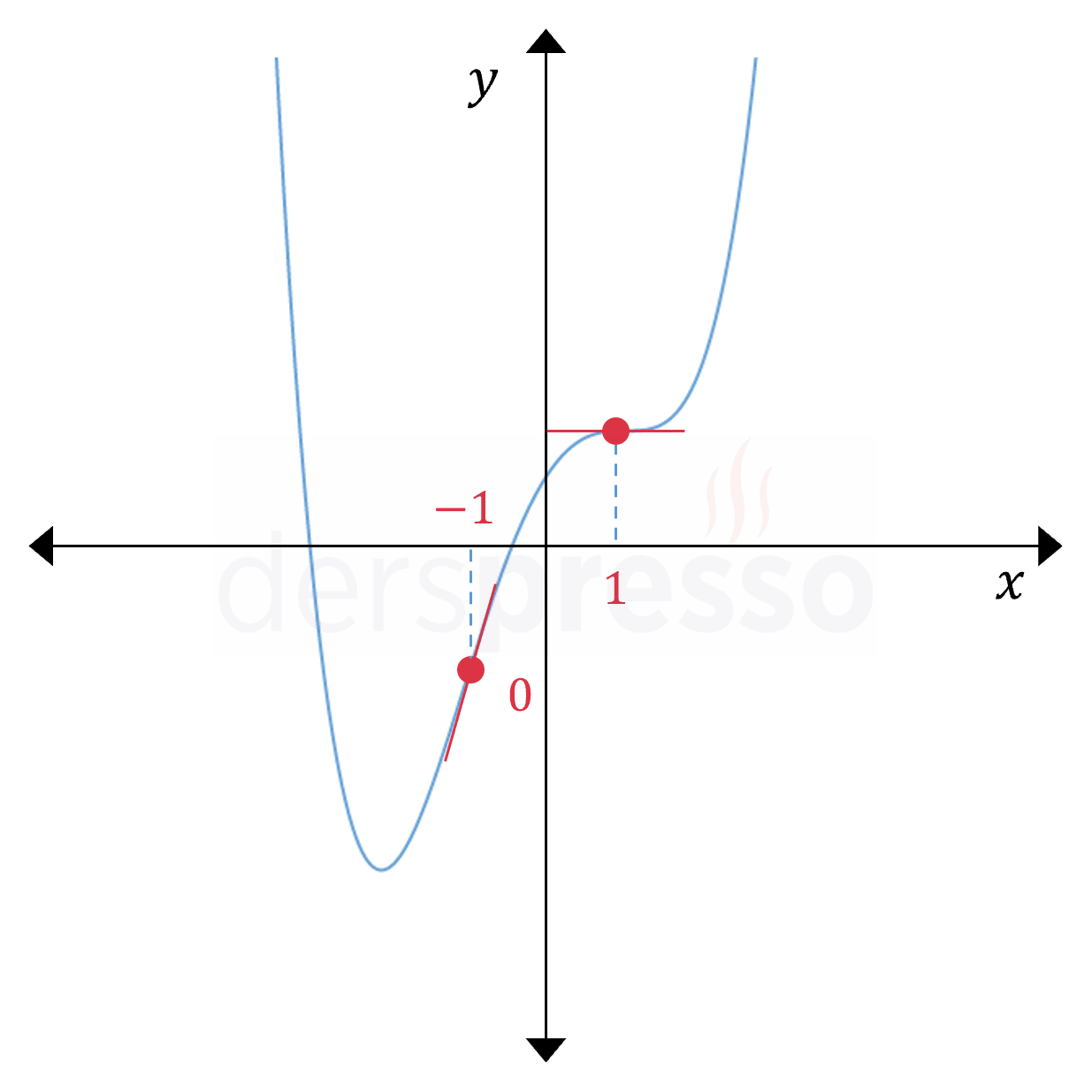
\( x = 1 \) noktasında birinci türev sıfır olduğu için bu nokta bir yatay (durağan) büküm noktasıdır. \( x = -1 \) noktası da durağan olmayan bir büküm noktasıdır.
Fonksiyon grafiği büküm noktaları işaretlenmiş şekilde aşağıda verilmiştir.
\( f(x) = 2x^3 + ax^2 - bx + 4 \) fonksiyonunun \( x = 1 \) noktasında yerel maksimum noktası ve \( x = -2 \) noktasında büküm noktası olduğuna göre \( f(-1) \) kaçtır?
Çözümü Göster