Parabolün Kökleri
\( f(x) \) bir parabol olmak üzere, \( f(x) = 0 \) denklemini sağlayan \( x \) değerleri parabolün kökleridir. Bu \( x \) değerleri aynı zamanda parabolün \( x \) eksenini kestiği noktaların apsis değerlerini verir.
İkinci dereceden denklemler konusunda incelediğimiz üzere, bir parabolün kökleri üç şekilde bulunabilir.
- Grafiği verilen bir parabolün \( x \) eksenini kestiği noktaların apsis değerleri parabolün reel kökleridir.
- Parabol denklemi çarpanlarına ayrıldığında her çarpanı sıfır yapan \( x \) değerleri parabolün kökleridir.
- Diskriminant formülü ile elde edilen değerler parabolün kökleridir.
Bir parabolün \( x \) eksenine göre durumu ve reel kökleri üç şekilde olabilir.
- 2 reel kök: Parabol \( x \) eksenini iki farklı noktada keser.
- 1 reel kök: Parabol \( x \) eksenini tek bir noktada (teğet) keser.
- 0 reel kök: Parabol \( x \) eksenini kesmez.
Bir parabolün bu üç durumdan hangisinde olduğu denklemin deltası (diskriminantı) hesaplanarak aşağıdaki şekilde bulunabilir.
\( y = ax^2 + bx + c \quad \) parabolün denklemi,
\( \Delta = b^2 - 4ac \quad \) denklemin deltası olmak üzere,
Parabol \( x \) eksenini;
\( \Delta \gt 0 \) ise iki noktada keser,
\( \Delta = 0 \) ise tek bir noktada (teğet) keser,
\( \Delta \lt 0 \) ise kesmez.
\( y = 3x^2 - 4x + 2 \)
\( \Delta = (-4)^2 - 4\cdot 3 \cdot 2 = -8\)
\( \Delta \lt 0 \) olduğu için parabol \( x \) eksenini kesmez.
Şimdi bu üç durumu daha detaylı inceleyelim.
Parabol x Eksenini İki Noktada Keser
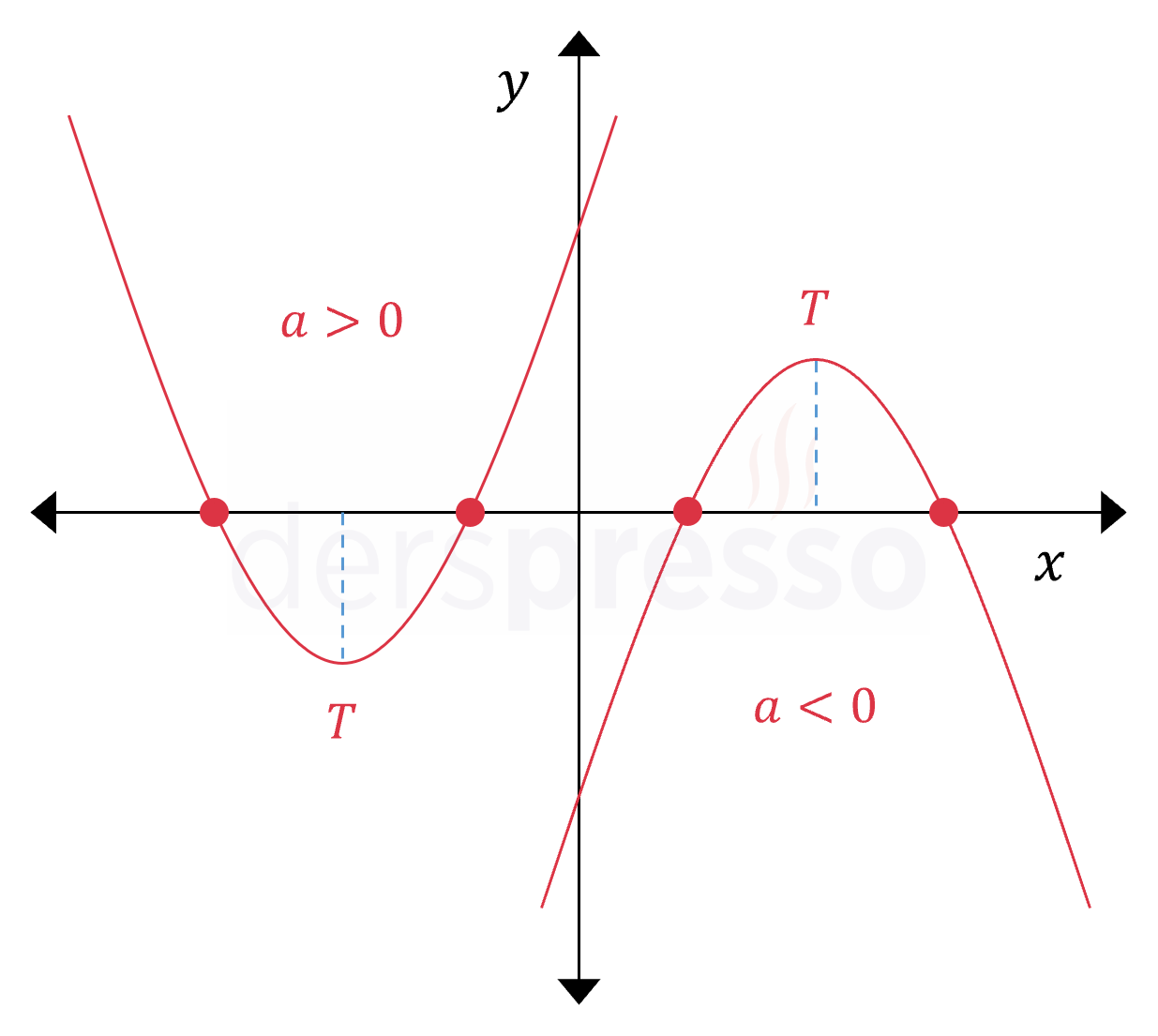
Bir parabol \( x \) eksenini \( x = x_1 \) ve \( x = x_2 \) şeklinde iki farklı noktada kesiyorsa aşağıdaki çıkarımlar yapılabilir.
- Parabolün deltası sıfırdan büyüktür.
- \( f(x) = 0 \) denkleminin birbirinden farklı iki reel kökü vardır.
- Parabol denklemi \( f(x) = a(x - x_1)(x - x_2) \) şeklinde çarpanlarına ayrılabilir.
- Parabolün bir kısmı \( x \) ekseninin üstünde, bir kısmı altında kalır, yani \( y \) hem pozitif hem negatif değer alır.
- Parabolün tepe noktasının apsis değeri parabolün \( x \) eksenini kestiği iki noktanın orta noktasının apsis değerine eşittir.
Parabol x Eksenini Tek Bir Noktada (Teğet) Keser
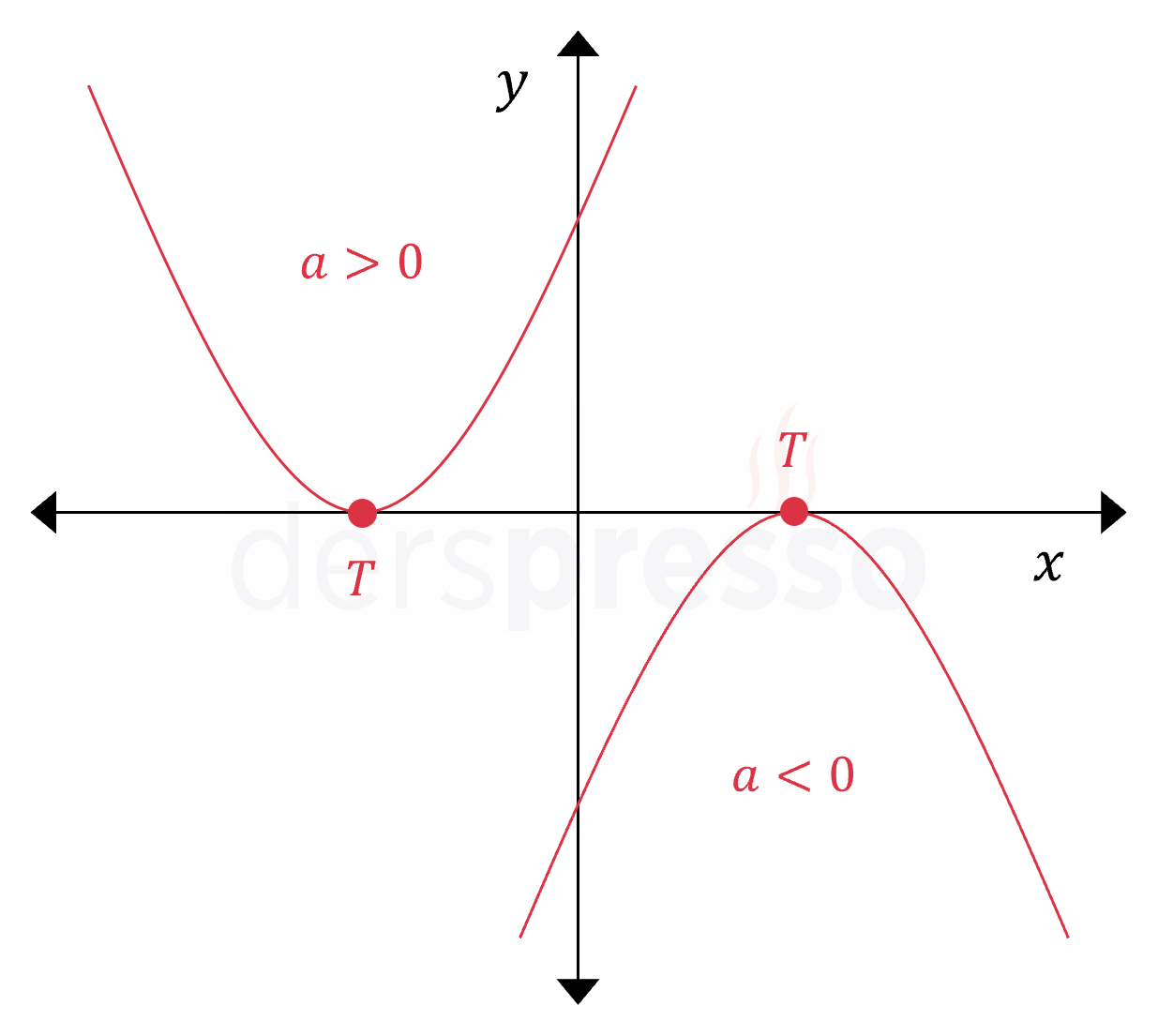
Bir parabol \( x \) eksenini \( x = x_1 \) şeklinde tek bir noktada kesiyorsa aşağıdaki çıkarımlar yapılabilir.
- Parabolün deltası sıfıra eşittir.
- \( f(x) = 0 \) denkleminin tek bir (iki katlı, çakışık) reel kökü vardır.
- Parabol denklemi \( f(x) = a(x - x_1)^2 \) şeklinde çarpanlarına ayrılabilir.
- \( a \gt 0 \) ise parabolün değeri her zaman sıfır ya da pozitiftir (\( f(x) \ge 0 \)), yani parabol negatif değer almaz.
- \( a \lt 0 \) ise parabolün değeri her zaman sıfır ya da negatiftir (\( f(x) \le 0 \)), yani parabol pozitif değer almaz.
- Parabolün tepe noktası parabolün \( x \) eksenini kestiği noktadır.
Parabol x Eksenini Kesmez
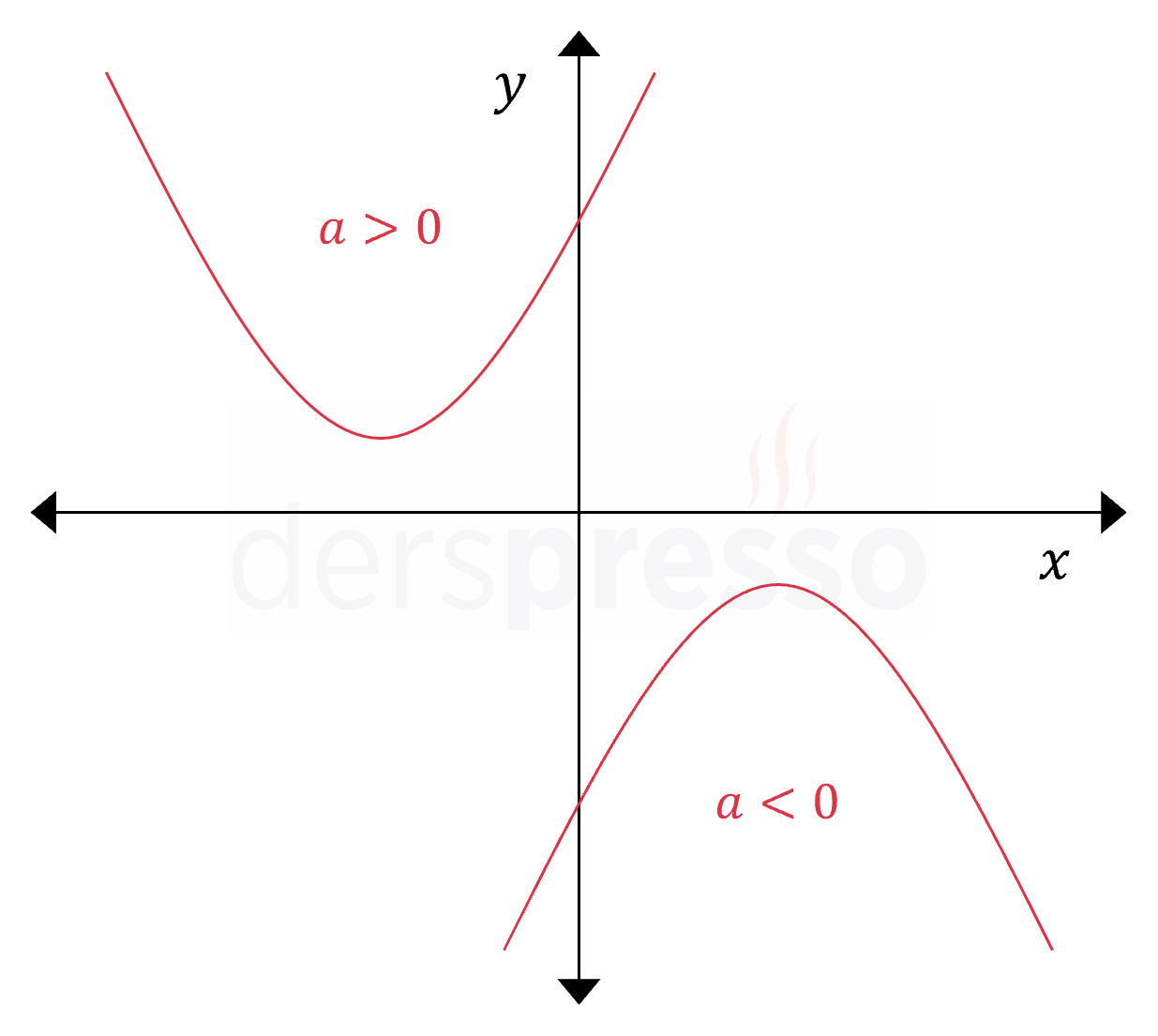
Bir parabol \( x \) eksenini kesmiyorsa aşağıdaki çıkarımlar yapılabilir.
- Parabolün deltası sıfırdan küçüktür.
- \( f(x) = 0 \) denkleminin reel kökü yoktur, birbirinin eşleniği iki karmaşık sayı kökü vardır.
- Parabol denklemi kökleri reel sayı olacak şekilde çarpanlarına ayrılamaz.
- \( a \gt 0 \) ise parabolün değeri her zaman pozitiftir (\( f(x) \gt 0 \)).
- \( a \lt 0 \) ise parabolün değeri her zaman negatiftir (\( f(x) \lt 0 \)).
Reel katsayılı ikinci dereceden bir denklemin tek bir karmaşık sayı kökü olamaz, denklemin karmaşık sayı kökü varsa bu kökler iki tane ve birbirinin eşleniği şeklinde olur.
Parabolün Kökleri ve Katsayıları
Bir parabolün kökleri ile denkleminin katsayıları arasında aşağıdaki ilişkiler vardır. Bu formüllerin nasıl türetildiği ile ilgili detaylı bilgi için ikinci dereceden denklemlerde kök katsayı ilişkisi sayfasını inceleyebilirsiniz.
| İfade | Formül |
|---|---|
| Kökler toplamı | \( x_1 + x_2 = -\dfrac{b}{a} \) |
| Kökler çarpımı | \( x_1 \cdot x_2 = \dfrac{c}{a} \) |
| Köklerin çarpmaya göre terslerinin toplamı | \( \dfrac{1}{x_1} + \dfrac{1}{x_2} = -\dfrac{b}{c} \) |
| Kökler farkının mutlak değeri | \( \abs{x_1 - x_2} = \dfrac{\sqrt{\Delta}}{\abs{a}} \) |
| Simetrik köklerde kökler toplamı | \( x_1 + x_2 = 0 \) |
Bunlara ek olarak, özdeşlikler kullanılarak bir parabol denkleminin kökleri arasında aşağıdaki ilişkiler kurulabilir.
\( x_1^2 + x_2^2 = (x_1 + x_2)^2 - 2x_1x_2 \)
\( x_1^3 + x_2^3 = (x_1 + x_2)(x_1^2 - x_1x_2 + x_2^2) \)
\( f(x) = 3x^2 - 4x + 2m + 1 \) fonksiyonunun grafiği \( x \) eksenine teğet ise \( m \) kaçtır?
Çözümü Göster\( f(x) = x^2 - 4x + m - 2 \) fonksiyonunun grafiği \( x \) eksenini iki noktada kesiyorsa \( m \) için geçerli değer aralığı nedir?
Çözümü Göster\( f(x) = x^2 - mx + 3m \) fonksiyonunun grafiği \( x \) eksenini kesmediğine göre \( m \) için geçerli değer aralığı nedir?
Çözümü Göster\( y = x^2 - (4m + 3)x + 16 \) parabolünün tepe noktasının \( x \) ekseni üzerinde olması için \( m \)'nin alabileceği değerler nelerdir?
Çözümü Göster\( y = x^2 - (m - 4)x - 2m - 1 \)
parabolünün tepe noktası \( y \) ekseni üzerinde olduğuna göre, parabolün \( x \) eksenini kestiği noktalar arasındaki uzaklığı bulunuz.
Çözümü Göster\( f: \mathbb{R} \to \mathbb{R} \)
\( f(x) = x^2 + 4x - 21 \)
fonksiyonunun \( x \) eksenini kestiği noktalar arasındaki uzaklık kaç birimdir?
Çözümü Göster\( f(x) = x^2 - 2x - 16 \)
parabolünün \( x \) eksenini kestiği noktalardan biri \( A(m, 0) \) ise, \( (m + 1)(m - 3) \) ifadesinin değeri kaçtır?
Çözümü Göster\( m \) ve \( n \) reel sayılar olmak üzere,
\( x^2 - mx + n = 0 \) denkleminin köklerinden biri \( (1 + i) \) ise \( m \cdot n \) çarpımı kaçtır?
Çözümü Göster\( f \) ikinci dereceden bir polinom fonksiyonu olup tüm reel sayılarda \( f(x) \le 0 \) olarak veriliyor.
\( f(3) = 0 \) ve \( f(8) = -20 \) olduğuna göre, \( f(-7) \) kaçtır?
Çözümü Gösterİkinci dereceden \( f \) fonksiyonunun katsayılar toplamı, kökler toplamı ve kökler çarpımı birbirine eşittir.
\( f(2) = 4 \) ise, \( f(1) \) kaça eşittir?
Çözümü Göster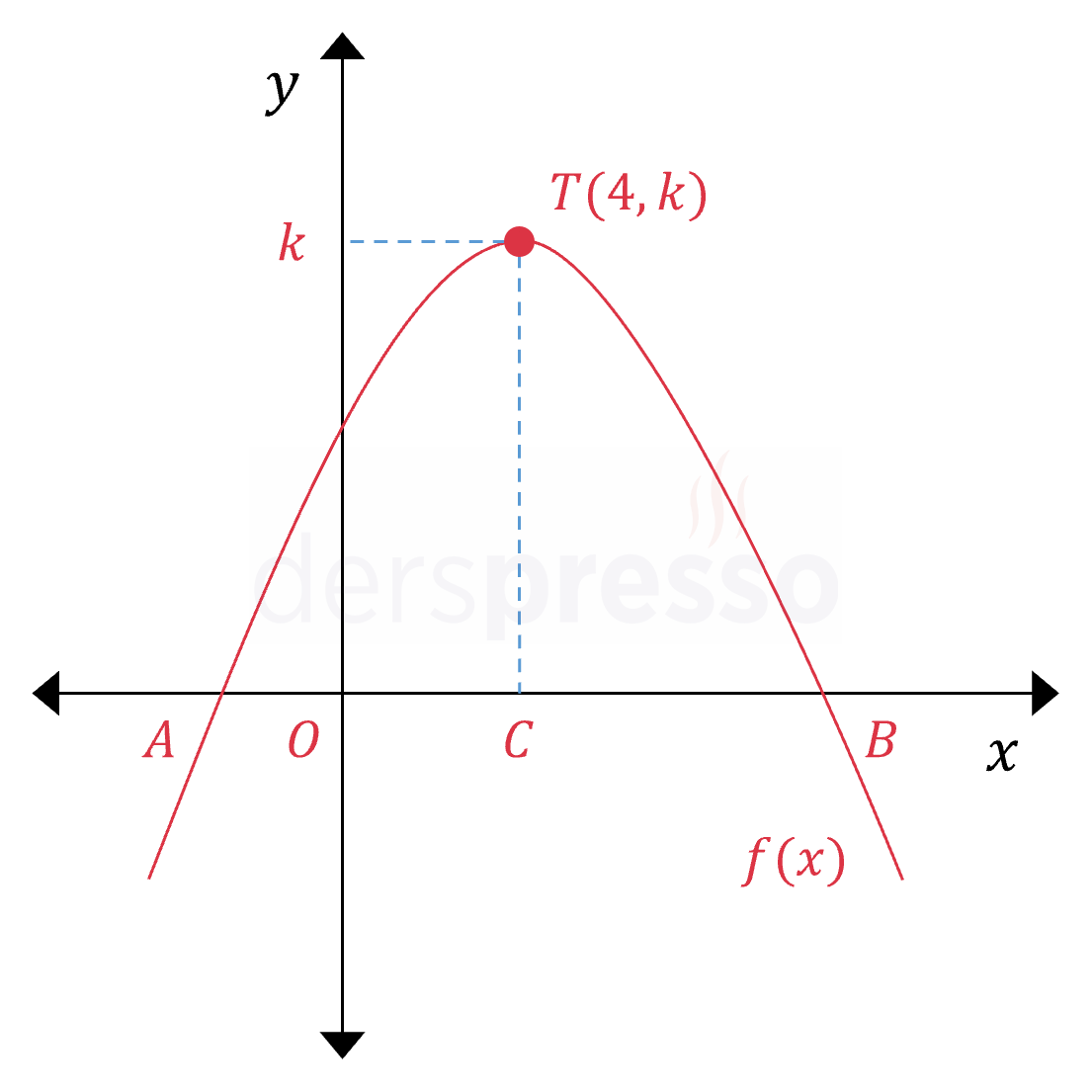
Yukarıda grafiği verilen parabolün tepe noktası \( T(4, k) \) noktasıdır.
\( \abs{OB} = 5 \cdot \abs{OA} \) olduğuna göre, \( A \) ve \( B \) noktalarının apsisi kaçtır?
Çözümü Göster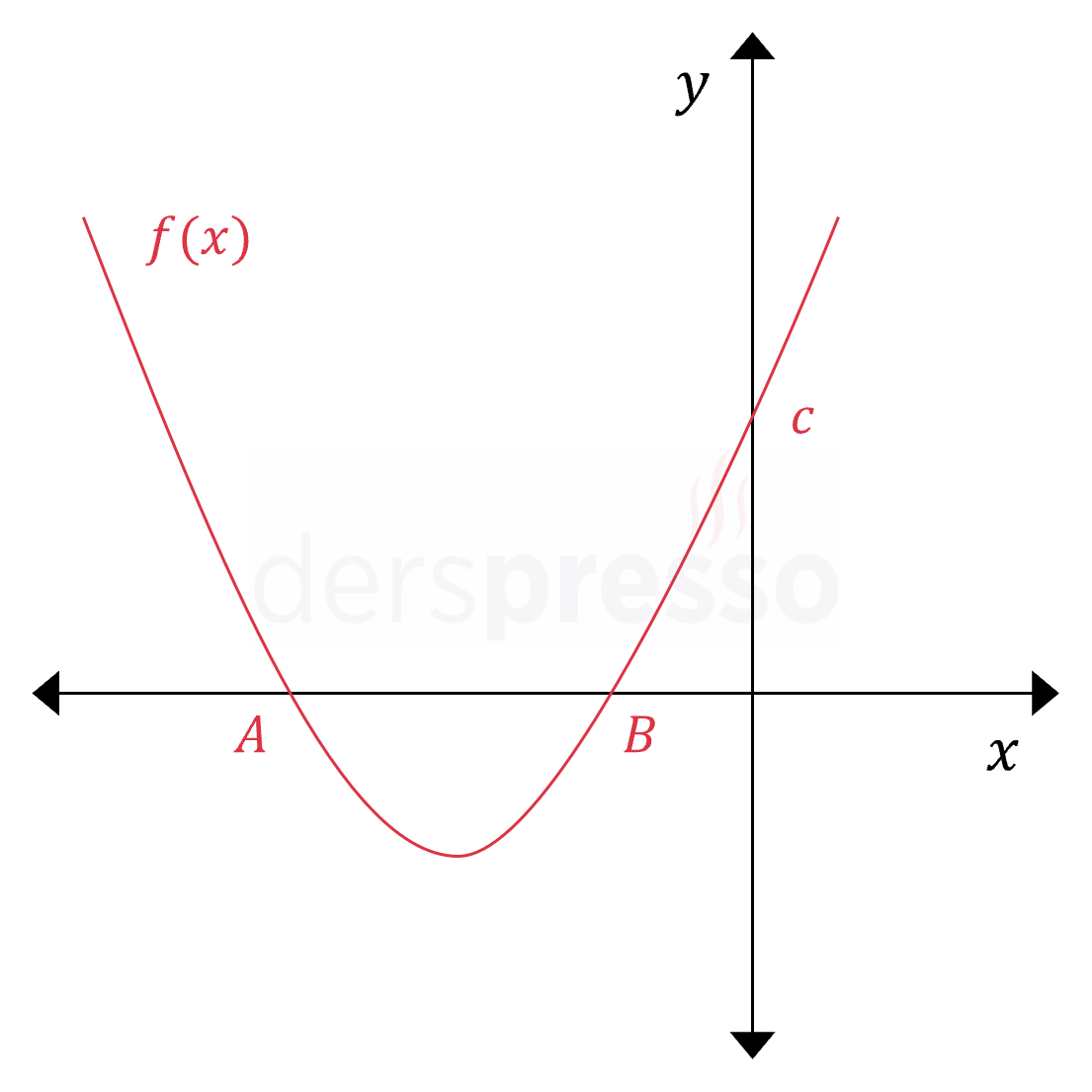
Yukarıdaki şekilde \( f(x) = x^2 + 5x + c \) parabolünün grafiği verilmiştir.
Parabolün \( x \) eksenini kestiği noktalar \( A \) ve \( B \) ve \( \abs{AB} = 1 \text{ br} \) olduğuna göre, parabolün \( y \) eksenini kestiği noktanın ordinatı kaçtır?
Çözümü GösterAşağıda \( f(x) = -x^2 + mx + n \) parabolü verilmiştir.
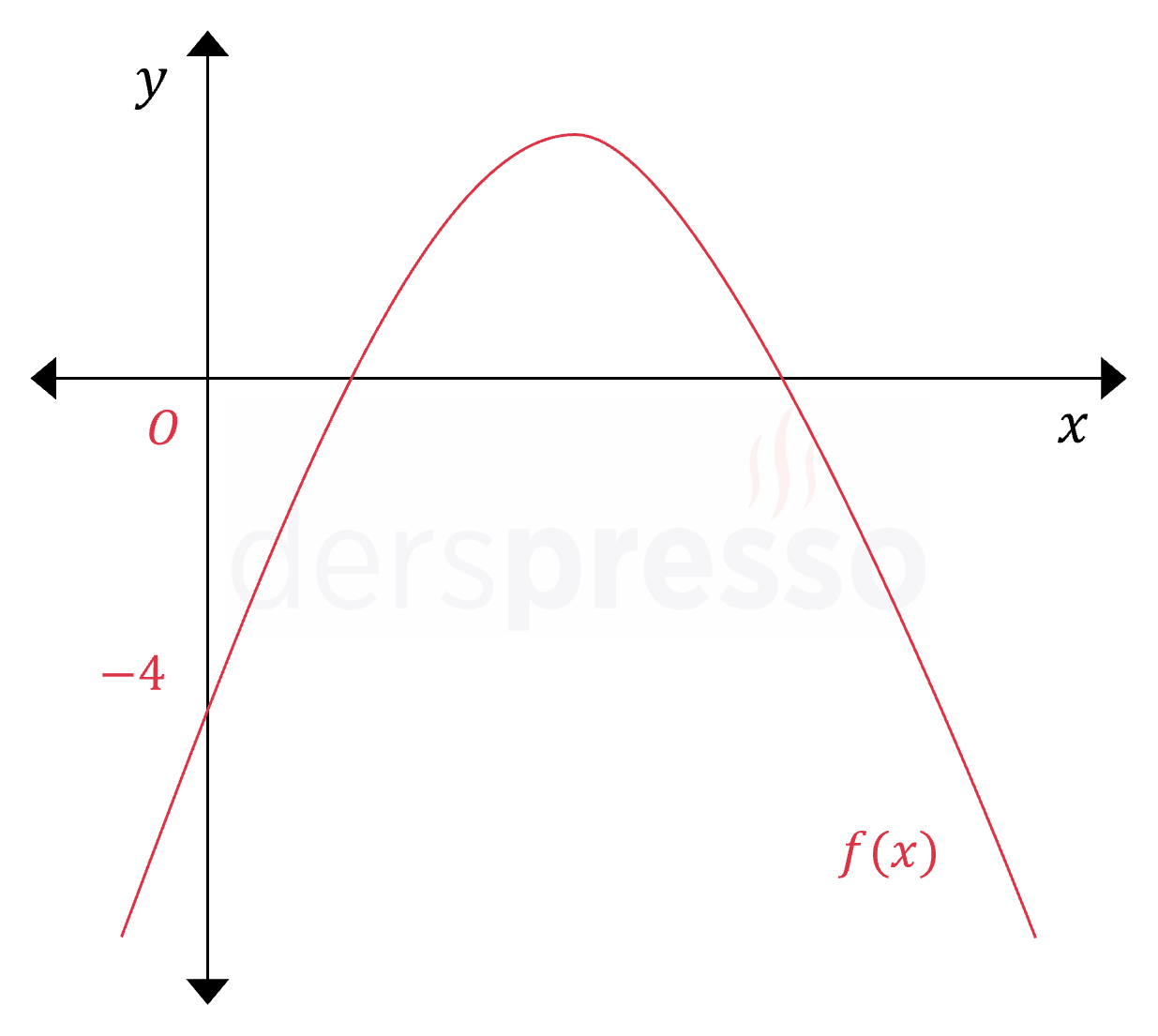
\( x_1 + x_2 = 3x_1 \cdot x_2 \) olduğuna göre, fonksiyonun alabileceği en büyük değer kaçtır?
Çözümü GösterAşağıda \( f(x) = -x^2 + 14x + 4m + 8 \) fonksiyonunun grafiği verilmiştir.
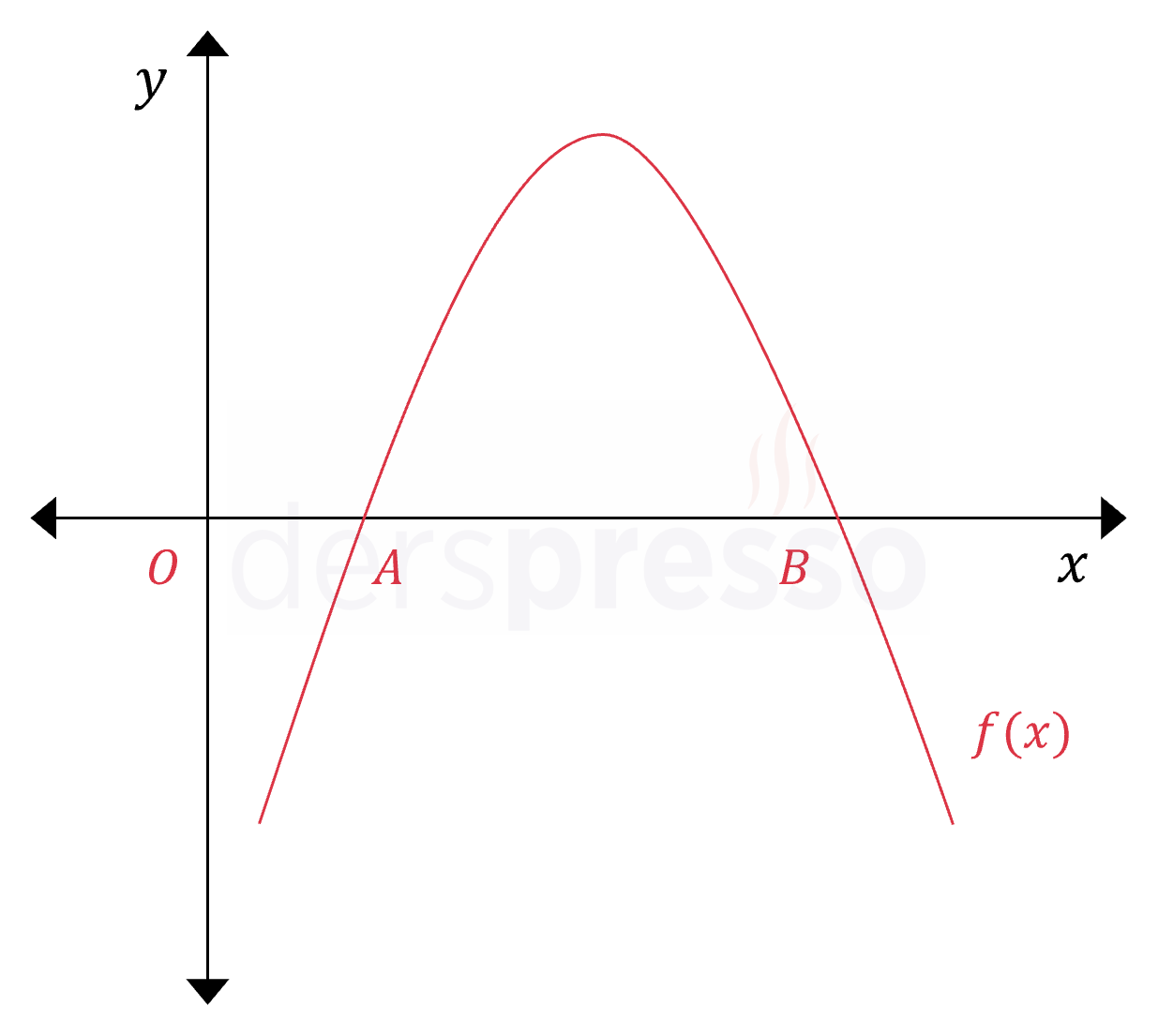
\( 5\abs{AO} = 2\abs{OB} \) olduğuna göre, \( m \) kaçtır?
Çözümü GösterAşağıda \( f(x) = x^2 - mx + 8 \) fonksiyonunun grafiği verilmiştir.
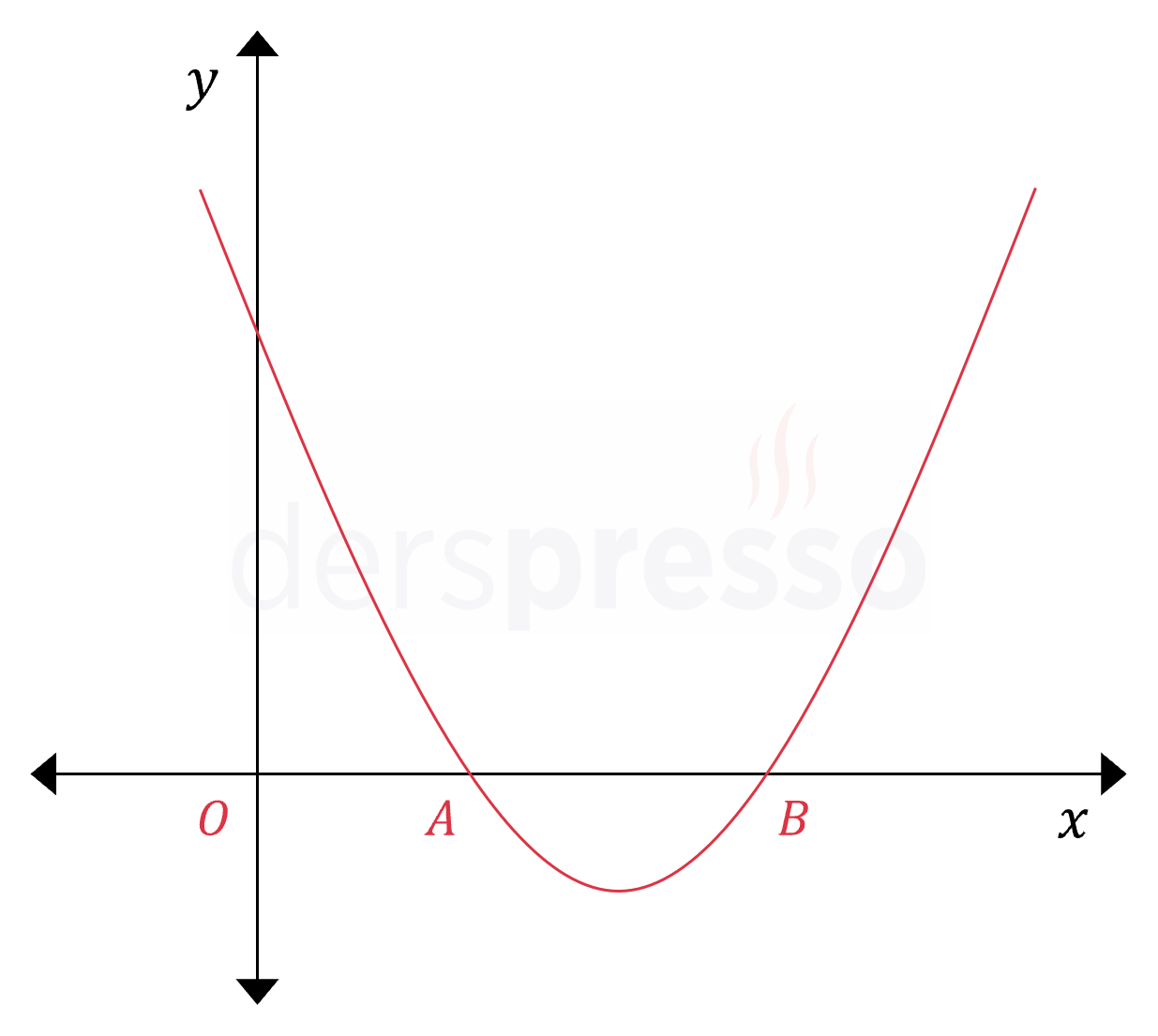
\( \abs{AB} = 2 \) olduğuna göre, \( f(5) \) kaçtır?
Çözümü Göster