Lineer Denklem Sistemi Tanımı
Lineer denklem sistemlerinin fizik ve bilgisayar başta olmak üzere bilim ve mühendislik alanlarında sayısız uygulaması vardır. Bunun iki önemli sebebi lineer denklem sistemlerinin çözümünün lineer olmayan sistemlere göre oldukça kolay olması ve (birinci sebeple bağlantılı olarak) gerçek hayattaki lineer olmayan bazı problemlerin lineer ilişkiler şeklinde modellenebilmesidir.
Lineer Denklemler
Aşağıdaki formda yazılabilen denklemlere \( n \) bilinmeyenli lineer denklem denir.
\( a_1, a_2, \ldots, a_n, b \in \mathbb{R} \) olmak üzere,
\( a_1x_1 + a_2x_2 + \ldots + a_nx_n = b \)
Bir bilinmeyenli lineer denklem:
\( 3x = -4 \)
İki bilinmeyenli lineer denklem:
\( 2x - 3y = 0 \)
Üç bilinmeyenli lineer denklem:
\( -x + 8y - 5z = 6 \)
Bu denklemde \( x_1, x_2, \ldots, x_n \) denklemin değişkenleri (bilinmeyenleri), \( a_1, a_2, \ldots, a_n \) katsayıları, \( b \) ise sabit terimidir.
Bir bilinmeyenli denklemlerde değişken sembolü olarak genellikle \( x \), iki bilinmeyenli denklemlerde \( x \) ve \( y \), üç bilinmeyenli denklemlerde \( x \), \( y \) ve \( z \) kullanılır. Daha çok sayıda bilinmeyenin olduğu durumlarda ise \( x_1, x_2, \ldots, x_n \) sembolleri kullanılır.
Lineer denklemler değişkenlerin 1 dışındaki kuvvetlerini (\( x^2, \sqrt{x}, \frac{1}{x} \) vb.) ve değişkenlerin çarpımını (\( x_1x_2 \) vb.) içermezler. Ayrıca bir lineer denklemde değişkenler trigonometrik, logaritmik fonksiyonların içinde ve üstel ifadelerin üssünde bulunamazlar. Buna göre aşağıdaki denklemler birer lineer denklem değildir.
\( x_1^2 - 3\sqrt{x_2} = 11 \)
\( \dfrac{1}{x_1} + \dfrac{1}{x_2} = 4 \)
\( 2x_1 + 5x_2 - 4x_1x_2 = 0 \)
\( \sin{x_1} - 3\ln{x_2} + 2^{x_3} = 1 \)
Bir \( (x_1, x_2, \ldots, x_n) = (s_1, s_2, \ldots, s_n) \) sıralı \( n \)'lisi \( n \) bilinmeyenli bir lineer denklemi sağlıyorsa bu lineer denklemin bir çözümüdür.
\( 2x_1 - 3x_2 + 4x_3 = -3 \)
\( (2, 1, -1) \) ve \( (0, 0, 0) \) üçlülerinin yukarıdaki denklemin birer çözümü olup olmadığını kontrol edelim.
\( (x_1, x_2, x_3) = (2, 1, -1) \) üçlüsünü denklemde yerine koyalım.
\( 2(2) - 3(1) + 4(-1) \stackrel{?}{=} -3 \)
\( -3 = -3 \)
Eşitlik sağlandığı için üçlü denklemin bir çözümüdür.
\( (x_1, x_2, x_3) = (0, 0, 0) \) üçlüsünü denklemde yerine koyalım.
\( 2(0) - 3(0) + 4(0) \stackrel{?}{=} -3 \)
\( 0 \ne -3 \)
Eşitlik sağlanmadığı için üçlü denklemin bir çözümü değildir.
Bir lineer denklemin tüm çözümlerinden oluşan kümeye o denklemin çözüm kümesi denir.
Lineer Denklem Sistemleri
Aynı değişkenleri içeren birden fazla lineer denklemden oluşan denklem grubuna lineer denklem sistemi denir.
\( a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n = b_1 \)
\( a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n = b_2 \)
\( \vdots \quad \vdots \quad \vdots \)
\( a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n = b_m \)
Üç bilinmeyenli üç denklemden oluşan lineer denklem sistemi:
\( x + 2y + z = 0 \)
\( 6x - 4y + 3z = 29 \)
\( 5x + 2z = 17 \)
Bir denklem sisteminin cebirsel yazılışında genel kural denklemlerde değişken içeren terimlerin eşitliğin sol tarafında, sabit terimlerin de sağ tarafında bulunmasıdır. Ayrıca değişkenlerin sırası tüm denklemlerde aynı olmalıdır. Denklemlerin hangi sırada listelendiğinin bir önemi yoktur.
Bir \( (x_1, x_2, \ldots, x_n) = (s_1, s_2, \ldots, s_n) \) sıralı \( n \)'lisi \( n \) bilinmeyenli bir lineer denklem sistemindeki tüm denklemleri sağlıyorsa bu lineer denklem sisteminin bir çözümüdür.
\( 5x_1 - 3x_2 + 2x_3 = 23 \)
\( 2x_1 + 4x_2 - x_3 = -3 \)
\( x_1 - 11x_2 - 6x_3 = 19 \)
\( (3, -2, 1) \) ve \( (-32, 9, -25) \) üçlülerinin yukarıdaki denklem sisteminin birer çözümü olup olmadığını kontrol edelim.
\( (x_1, x_2, x_3) = (3, -2, 1) \) üçlüsünü denklemlerde yerine koyalım.
\( 5(3) - 3(-2) + 2(1) = 23 \)
\( 2(3) + 4(-2) - 1 = -3 \)
\( 3 - 11(-2) - 6(1) = 19 \)
Üç denklemde de eşitlik sağlandığı için üçlü denklem sisteminin bir çözümüdür.
\( (x_1, x_2, x_3) = (-32, 9, -25) \) üçlüsünü üç denklemlerde yerine koyalım.
\( 5(-32) - 3(9) + 2(-25) = -237 \ne 23 \)
\( 2(-32) + 4(9) - (-25) = -3 \)
\( -32 - 11(9) - 6(-25) = 19 \)
2. ve 3. denklemlerde sağlansa da 1. denklemde eşitlik sağlanmadığı için üçlü denklem sisteminin bir çözümü değildir.
Bir lineer denklem sisteminin tüm çözümlerinden oluşan kümeye o denklem sisteminin çözüm kümesi denir. İki lineer denklem sisteminin çözüm kümeleri aynı ise bu denklem sistemleri birbirine denktir.
Farklı Çözüm Durumları
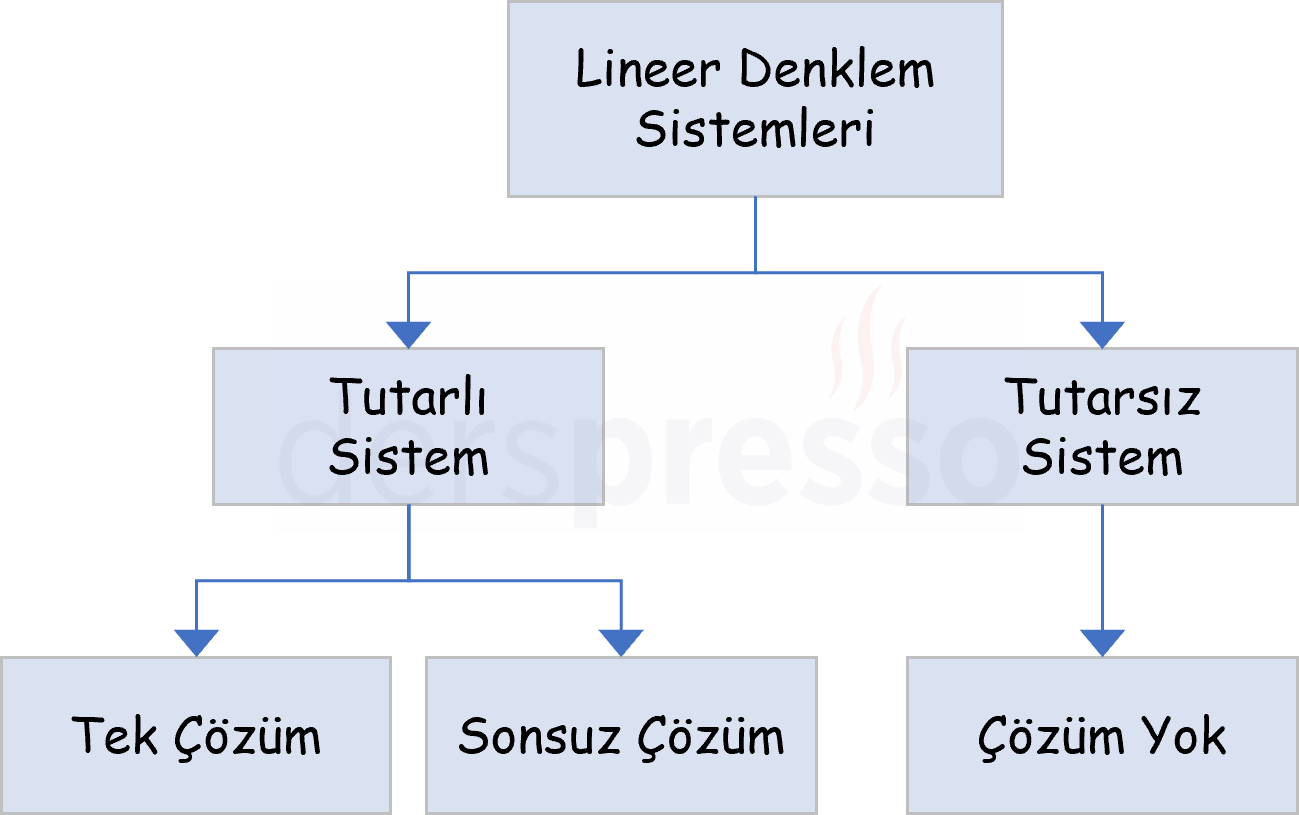
Bir lineer denklem sisteminin çözüm kümesi ile ilgili olarak aşağıdaki üç durumdan sadece biri doğrudur.
- Sistemin tek bir çözümü vardır.
- Sistemin sonsuz çözümü vardır.
- Sistemin çözümü yoktur.
İki bilinmeyenli bir lineer denklem analitik düzlemde bir doğru ifade eder ve bu doğru üzerindeki tüm noktalar denklemin birer çözümüdür. İki bilinmeyenli bir lineer denklem sisteminin çözümü sistemdeki denklemlerin grafiklerinin (varsa) kesişim noktasıdır. Buna göre, \( x \) ve \( y \) değişkenlerinden ve iki denklemden oluşan bir sistem için bu üç farklı durum grafiksel olarak aşağıdaki şekilde gösterilebilir.

Bir lineer denklem sisteminin tek bir ya da sonsuz sayıda çözümü varsa o denklem sistemi tutarlıdır, bir çözümü yoksa tutarsızdır.